数据结构(C语言版)严蔚敏-＞排序

@

目录

• 1. 插入排序
  • 1.1 直接插入排序
  • 1.2 折半插入排序
  • 1.3 希尔排序(Shell Sort)
• 2.交换排序
  • 2.1 冒泡排序
  • 2.2 快速排序
• 3. 选择排序
  • 3.1 简单选择排序
  • 3.2 堆排序
    • 3.2.1 大根堆
    • 3.2.2 小根堆

1. 插入排序

插入排序是一种简单直观的排序方法，其基本思想是每次将一个待排序的记录按其关键字大小插入前面已排好序的子序列，直到全部记录插入完全。

1.1 直接插入排序

直接插入排序运行动态图如下：



参考代码如下：

#include <stdio.h>

void InsertSort(int[],int);
// 无哨兵的插入排序
void PrintData(int[],int);
void InsertSort2(int[],int);
// 有哨兵的插入排序,数组下标为0处不存储数据元素
void PrintData2(int[],int);

int main(){

    int A1[] = {49,38,65,97,76,13,27,49};
    InsertSort(A1,8);
    PrintData(A1,8);

    printf("\n");
    int A2[] = {0,49,38,65,97,76,13,27,49};
    InsertSort2(A2,8);
    PrintData2(A2,8);
    return 0;
}

void InsertSort(int A[],int n){
    int i,j,temp;
    for(i=1;i<n;i++)
        if(A[i]<A[i-1]){
            temp = A[i];
            for(j=i-1;j>=0&&temp<A[j];--j)
                A[j+1] = A[j];
            A[j+1] = temp;
        }
}

void InsertSort2(int A[],int n){
    int i,j;
    for(i=2;i<=n;i++)
        if(A[i]<A[i-1]){
            A[0] = A[i];
            for(j=i-1;A[0]<A[j];--j)
                A[j+1] = A[j];
            A[j+1] = A[0];
        }
}

void PrintData(int A[],int n){
    for(int i=0;i<n;i++)
        printf("%d\t",A[i]);
}

void PrintData2(int A[],int n){
    for(int i=1;i<=n;i++)
        printf("%d\t",A[i]);
}

运行结果如下：

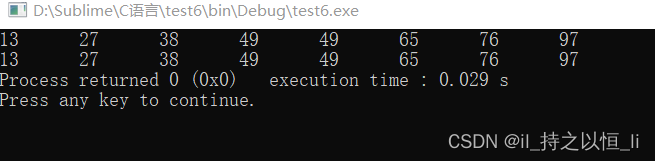
• 算法的空间复杂度：O(1)
• 算法的时间复杂度：O(n^2)
• 稳定性：由于每次插入元素时总是从后向前比较再移动，所以不会出现相同元素相对位置发生变化的情况，即直接插入是一种稳定的排序算法。

1.2 折半插入排序

参考代码如下：

void InsertSort3(int A[],int n){
    int i,j,low,high,mid;
    for(i=2;i<=n;i++){
        A[0] = A[i];
        low = 1,high = i-1;
        while(low<=high){
            mid = (low+high)/2;
            if(A[mid] > A[0])
                high = mid - 1;
            else
                low = mid + 1;
        }

        for(j=i-1;j>=high+1;--j)
            A[j+1] = A[j];
        A[high+1] = A[0];
    }
}

• 算法时间复杂度：折半插入排序的时间复杂度为O(n^2)，但对于数据量不是很大的排序表，折半插入排序往往能表现出很好的性能。

1.3 希尔排序(Shell Sort)

希尔排序的基本思想是：先将待排序表分成L[i,i+d,i+2d,..,i+kd]的“特殊”子表，即把相隔某个“增量”的记录组成一个子表，对各个子表分别进行直接插入排序，当整个表中的元素已呈“基本有序”时，再对全体记录进行一次直接插入排序。

参考代码如下：

void ShellSort(int A[],int n){
    // 希尔排序
    int i,j,dk;
    for(dk=n/2;dk>=1;dk/=2){
        // 步长变化
        for(i=dk+1;i<=n;i++){
            if(A[i] < A[i-dk]){
                A[0] = A[i];
                // A[0]元素只是暂存元素，不是哨兵
                for(j=i-dk;j>0&&A[j]>A[0];j-=dk)
                    A[j+dk] = A[j]; // 记录后移，查找插入的位置
                A[j+dk] = A[0]; // 插入
            }
        }
    }
}

• 算法的空间复杂度：O(1)
• 算法的时间复杂度：希尔排序的时间复杂度约为O(n^1.3)，在最坏情况下希尔排序的时间复杂度为O(n^2).
• 稳定性：当相同关键字的记录被划分到不同的子表时，可能会改变它们之间的相对次序，因此希尔排序是一种不稳定的排序方法。

2.交换排序

2.1 冒泡排序

基本思想：从后往前（或从前往后）两两比较相邻元素的值，若为逆序（即A[i-1]>A[i]），则交换它们，直到序列比较完毕！

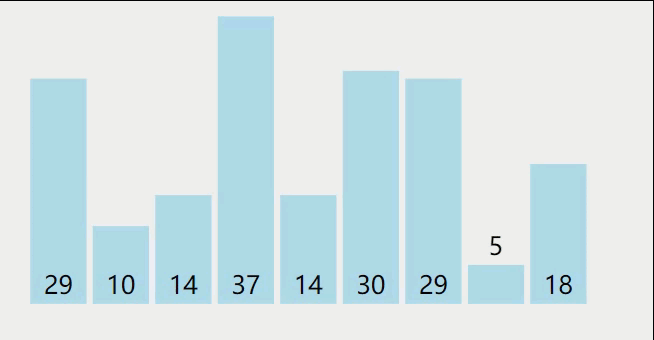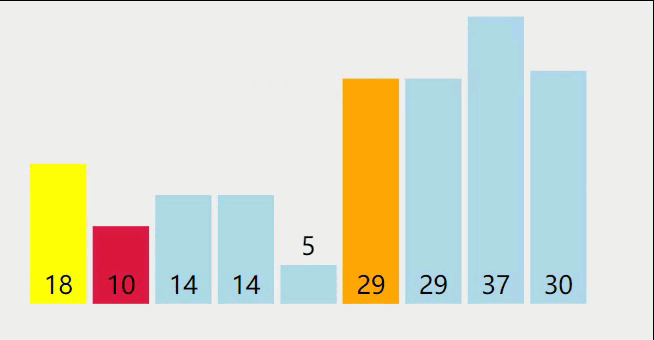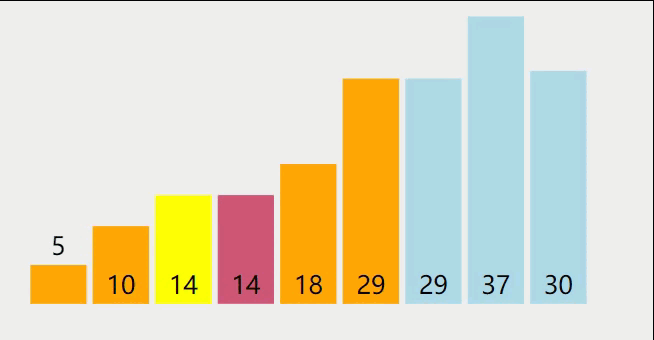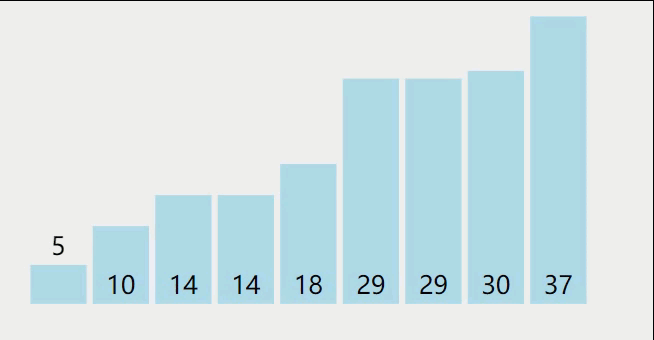
下图为一个冒泡排序的过程(从后往前两两比较相邻元素的值【即先把小的元素往前排】)。



到了第五趟结束后没有发生交换，说明表已经有序。

下图为另外一个冒泡排序的过程(从前往后两两比较相邻元素的值【即先把大的元素往后排】)



参考代码如下：

// 冒泡排序
void BubbleSort(int A[],int n){
    int i,j,temp;
    bool flag;
    for(i=0;i<n-1;i++){
        flag = false;
        for(j=n-1;j>i;j--){
            if(A[j-1]>A[j]){
                temp = A[j-1];
                A[j-1] = A[j];
                A[j] = temp;
                flag = true;
            }
        }
        if(!flag)
            return;
        // 某一趟遍历后没有发生交换，说明表已经有序
    }
}

• 算法的空间复杂度：O(1)
• 算法的时间复杂度：O(n^2)
• 算法的稳定性：由于i>j且A[i]=A[j]时，不会发生交换，因此冒泡排序是一种稳定的排序方法。
• 比较次数：n(n-1)/2
• 移动次数：3n(n-1)/2

2.2 快速排序

基本思想：在待排序表L[1,n]中任取一个元素pivot作为枢轴（或基准，通常取首元素），通过一趟排序将待排序表划分为独立的两部分L[1,k-1]和L[k+1,n]，使得L[1,k-1]中的所有元素小于pivot，L[k+1,n]中的所有元素大于等于pivot，则pivot放在了最终位置L(k)上，这个过程称为一趟快速排序。然后分别递归地对两个子表重复上述过程，直至每部分内只有一个元素为止，即所有元素放在了其最终的位置上。

快速排序过程如下：



参考代码如下：

int Partition(int A[],int low,int high){
    int pivot = A[low];
    while(low<high){
        while(low<high&&A[high]>=pivot)
            high--;
        A[low] = A[high];
        while(low<high&&A[low]<=pivot)
            low++;
        A[high] = A[low];
    }
    A[low] = pivot;
    return low;
}

void QuickSort(int A[],int low,int high){
    if(low<high){
        int pivotpos = Partition(A,low,high);
        QuickSort(A,low,pivotpos-1);
        QuickSort(A,pivotpos+1,high);
    }
}

• 空间复杂度：最好情况下为O(logn)，最坏情况下为O(n)
• 时间复杂度：最好为O(nlogn)，最坏为O(n^2)，平均情况下为O(nlogn)
• 稳定性：在划分算法中，若右端区间有两个关键字相同，且均小于基准值的记录，则在交换到左侧区间后，它们的相对位置发生了变化，即快速排序是一种不稳定的排序方法。
• 快速排序是所有排序内部排序算法中平均性能最优的排序算法。

【注】：在快速排序算法中，并不产生有序子序列，但每趟排序后会将枢轴（基准）元素放到其最终的位置上。

3. 选择排序

选择排序的基本思想是：每一趟（第i趟）在后面的n-i+1（i=1,2,,...,n-1）个待排序元素中选取关键字最小的元素，作为有序子序列的第i个元素，直到n-1趟做完，待排序元素只剩下一个，就不用再选了。

3.1 简单选择排序

简单选择排序算法思想：假设排序表为L[1,n]，第i趟排序即从L[i,n]中选取关键字最小的元素与L(i)交换，每一趟排序可以确定一个元素的最终位置，这样经过n-1趟排序就可以使得整个排序表有序

参考代码如下：

void SelectSort(int A[],int n){
    int i,j,min_index,temp;
    for(i=0;i<n-1;i++){
        min_index = i;
        for(j=i+1;j<n;j++){
            if(A[j]<A[min_index]){
                min_index = j;
            }
        }
        if(min_index!=i){
            temp = A[i];
            A[i] = A[min_index];
            A[min_index] = temp;
        }
    }
}

• 空间复杂度：O(1)
• 时间复杂度：O(n^2)
• 稳定性：简单选择排序是一种不稳定的排序方法
• 使用性：既可以用于顺序表，也可以用于链表
• 比较次数：n(n-1)/2

3.2 堆排序

堆定义如下：n个关键字序列L[1,n]称为堆，当且仅当该序列满足：

(1)L[i]>L[2i]且L[i]>L[2i+1]或

(2)L[i]<L[2i]且L[i]<L[2i+1]

可以将该一维数组称为一棵完全二叉树，满足条件(1)的堆称为大根堆（大顶堆），大根堆的最大元素存放在根节点，且其任一非根节点的值小于等于其双亲节点值。满足条件(2)的堆称为小根堆（小顶堆），根节点是最小元素。

• 利用大根堆进行排序得到的序列为升序序列
• 利用小根堆进行排序得到的序列为降序序列

3.2.1 大根堆

建立大根堆的算法如下：

void BuildMaxHeap(int A[],int len);
int main(){
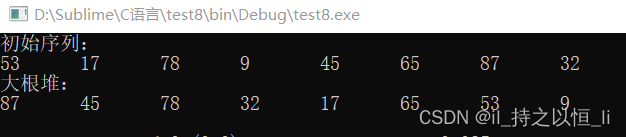
    int A[] = {0,53,17,78,9,45,65,87,32};
    printf("初始序列：\n");
    for(int i=1;i<=8;i++){
        printf("%d\t",A[i]);
    }
    printf("\n");
    BuildMaxHeap(A,8);
    printf("大根堆：\n");
    for(int i=1;i<=8;i++){
        printf("%d\t",A[i]);
    }
    printf("\n");
    return 0;
}

void HeadAdjust(int A[],int k,int len){
    A[0] = A[k]; // A[0]暂存子树的根节点
    int i;
    for(i=2*k;i<=len;i*=2){
        if(i<len&&A[i]<A[i+1])
            i++;
        // 取key较大的子节点的下标
        if(A[0]>=A[i]) break;
        else{
            A[k] = A[i];  // 将A[i]调整到双亲节点上
            k = i;    // 修改k值，以便继续向下筛选
        }
    }
    A[k] = A[0];
}

void BuildMaxHeap(int A[],int len){
    for(int i=len/2;i>0;i--){
        HeadAdjust(A,i,len);
    }
}

运行结果：



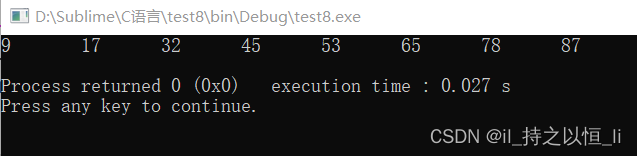
推排序算法如下：

void HeapSort(int A[],int len){
    BuildMaxHeap(A,len);
    int i,temp;
    for(i=len;i>1;i--){
        temp = A[1];
        A[1] = A[i];
        A[i] = temp;
        HeadAdjust(A,1,i-1);
    }
}

运行结果：

3.2.2 小根堆

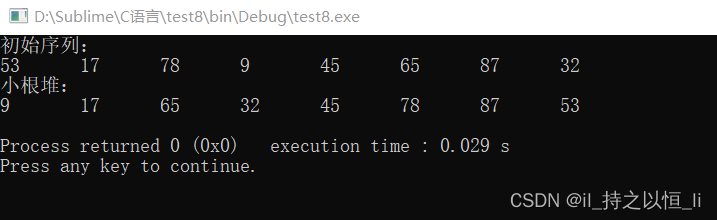
建立小根堆的算法如下：

void HeadAdjust2(int A[],int k,int len){
    A[0] = A[k];
    int i;
    for(i=2*k;i<=len;i*=2){
        if(i<len&&A[i]>A[i+1])
            i++;
        // 取key较小的子节点下标
        if(A[0]<=A[i])
            break;
        else{
            A[k] = A[i];
            k = i;
        }
    }
    A[k] = A[0];
}

void BuildMinHeap(int A[],int len){
    for(int i=len/2;i>0;i--){
        HeadAdjust2(A,i,len);
    }
}

运行结果：



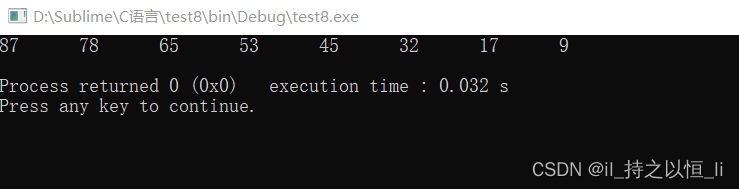
堆排序算法如下：

void HeapSort2(int A[],int len){
    BuildMinHeap(A,len);
    int i,temp;
    for(i=len;i>1;i--){
        temp = A[1];
        A[1] = A[i];
        A[i] = temp;
        HeadAdjust2(A,1,i-1);
    }
}

运行结果：

• 空间复杂度：O(1)
• 时间复杂度：O(nlogn)
• 稳定性：堆排序算法是一种不稳定排序方法