红黑树（map与unorder_map）B B+树

红黑树（map）

这个里面有插入的几种方式：红黑树性质的理解

先说性质，1 每个节点要么红要么黑，2 一个节点为红色，左右两个孩子都是黑， 3 根节点是黑， 4 每个叶子（nil）节点都是黑色， 5 任意一个节点，到叶子节点的所有简单路径，黑色节点的数量是一样的。（黑高）

再说为什么用红黑树，不用avl，红黑树的优势在于删除（最多旋3次），添加（最多旋2次），avl可能要在回溯过程中弄log次。红黑树的高最大能2*lg(n+1)，查询不如avl。 红黑树高度上限(2lg(n+1)证明.

关于为什么是三次和两次：红黑树最多三次旋转达到平衡

map用的是红黑树，unorder_map用的是哈希表，差别：map用operator <来比较大小，出来是有序的。而unorder_map是比较hash过后的值进行比较，输出不是有序的。

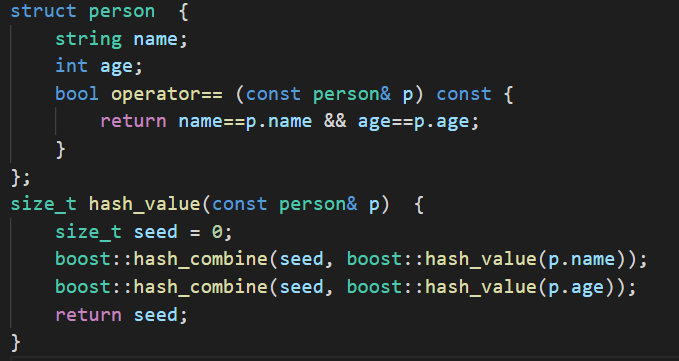
用法的区别就是，stl::map 的key需要定义operator< 。 而boost::unordered_map需要定义hash_value函数并且重载operator==，因为hash值相等不代表数据相等。

参考：map，hash_map和unordered_map 实现比较

B与B+树

B树：叶子所在层数是一样的，关键字非递减，搜索相当于二分查找，节点包含关键字信息。是平衡树。

B+树：关键字非递减，基于B Tree和叶子节点顺序访问指针实现，优势在于顺序访问指针提高区间查询性能。

红黑树等平衡性也可以用来实现索引，但文件系统和数据库普遍采用B+树作为索引结构，原因有二：

• 更少的查找次数
• 利用磁盘预读特性

• B+树还有一个最大的好处，方便扫库，B树必须用中序遍历的方法按序扫库，而B+树直接从叶子结点挨个扫一遍就完了，B+树支持range-query非常方便，而B树不支持。这是数据库选用B+树的最主要原因。
• 因为B+树的非叶子节点不用存数据，只需要存key，所以一个节点能够存储更大范围的区间。