最小生成树MST算法（Prim、Kruskal）

最小生成树MST（Minimum Spanning Tree）

(1)概念

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边，所谓一个 带权图 的最小生成树，就是原图中边的权值最小的生成树 ，所谓最小是指边的权值之和小于或者等于其它生成树的边的权值之和。

(2)性质

一个连通图可以有多个生成树；
一个连通图的所有生成树都包含相同的顶点个数和边数；
生成树当中不存在环；
移除生成树中的任意一条边都会导致图的不连通，生成树的边最少特性；
在生成树中添加一条边会构成环。
对于包含n个顶点的连通图，生成树包含n个顶点和n-1条边；
对于包含n个顶点的无向完全图最多包含 $n^{n-2}$ 颗生成树。

(3)应用

例如：要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树

MST算法之Prim

算法参考地址:Prim的最小生成树（MST）|贪婪的算法-5 - 极客 (geeksforgeeks.org)

Prim算法的流程

1）创建一组 mstSet，用于跟踪 MST 中已包含的顶点。 2）为输入图中的所有顶点分配一个键值。将所有键值初始化为 INFINITE。为第一个顶点分配键值为 0，以便首先选取它。 3）虽然 mstSet 不包括所有顶点 ....a）选择一个在 mstSet 中不存在且具有最小键值的顶点 u。 ....b）将 u 包含在 mstSet 中。 ....c）更新 u 的所有相邻顶点的键值。要更新键值，请循环访问所有相邻的顶点。对于每个相邻的顶点 v，如果边 u-v 的权重小于 v 的前一个键值，则将键值更新为 u-v 的权重使用键值的想法是从剪切中选取最小权重边。键值仅用于尚未包含在 MST 中的折点，这些折点的键值表示将它们连接到 MST 中包含的折点集的最小权重边。

让我们通过以下示例来理解：

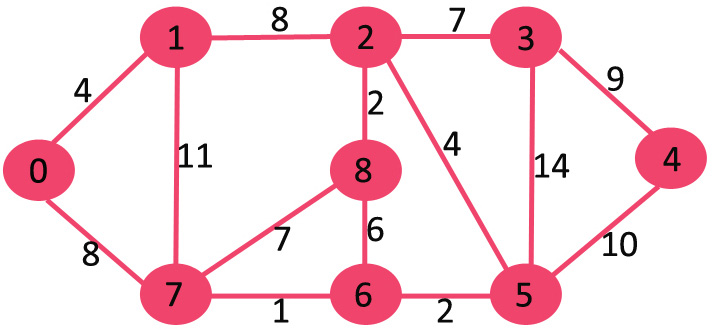
设置的 mstSet 最初是空的，分配给顶点的键是 {0， INF， INF， INF， INF， INF， INF， INF}，其中 INF 表示无限。现在选取具有最小键值的顶点。选取顶点 0，将其包含在 mstSet 中。因此，mstSet 变得{0}。包含到 mstSet 后，更新相邻顶点的键值。相邻顶点 0 为 1 和 7。1 和 7 的键值将更新为 4 和 8。下图显示顶点及其键值，仅显示具有有限键值的顶点。MST 中包含的顶点以绿色显示。

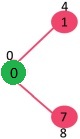
选取具有最小键值且尚未包含在 MST 中（不在 mstSET 中）的顶点。选取顶点 1 并将其添加到 mstSet。所以 mstSet 现在变成 {0， 1}。更新相邻顶点 1 的键值。顶点 2 的键值变为 8。

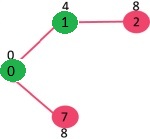
选取具有最小键值且尚未包含在 MST 中（不在 mstSET 中）的顶点。我们可以选择顶点7或顶点2，让顶点7被选中。所以 mstSet 现在变成 {0， 1， 7}。更新相邻顶点 7 的键值。顶点 6 和 8 的键值变为有限（分别为 1 和 7）。

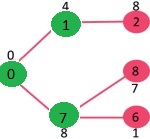
选取具有最小键值且尚未包含在 MST 中（不在 mstSET 中）的顶点。选取顶点 6。所以 mstSet 现在变成 {0， 1， 7， 6}。更新相邻顶点 6 的键值。顶点 5 和 8 的键值将更新。

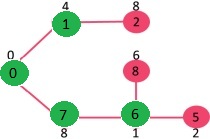
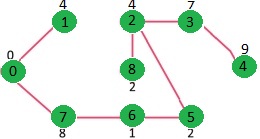
我们重复上述步骤，直到 mstSet 包含给定图形的所有顶点。最后，我们得到下图。

Prim算法的实现(golang)

prim算法的思想和Dijkstra很相似,在理解Dijkstra算法的前提下,理解Prim算法及其实现都会变得非常容易

//graph 中值为math.MaxInt的值为不可达
func prim(graph [][]int, randomVertex int) int {
   n := len(graph)
   //图中已经遍历到的顶点到未遍历的顶点的最短的距离
   dist := make([]int, n)
   //图中的顶点是否被访问过
   visit := make([]bool, n)
   //最小生成书的路径和
   res := 0

   curIdx := randomVertex

   //标记初始访问节点
   visit[curIdx] = true
   //初始化当前节点到未访问节点的距离
   for i := 0; i < n; i++ {
      dist[i] = graph[curIdx][i]
   }

   //由于已经初始化一个节点，所以只需便利n-1次
   for i := 1; i < n; i++ {
      minor := math.MaxInt
      for j := 0; j < n; j++ {
         //寻找与已存在节点相接的最短距离的节点
         if !visit[j] && dist[j] < minor {
            minor = dist[j]
            curIdx = j
         }
      }

      //标记到最短距离的节点为已访问
      visit[curIdx] = true
      //最短路径值求和
      res += minor

      //重新初始化已访问节点到未访问节点的距离
      for j := 0; j < n; j++ {
         /**
         仅更新没有访问过的节点且节点小于当前距离的节点
         (因为如果graph[curIdx][j]> dist[j]的话，说明当前已经有节点到节点j的距离更小，
         所以此边(graph[curIdx][j])永远也不会被用到)
         */
         if !visit[j] && graph[curIdx][j] < dist[j] {
            dist[j] = graph[curIdx][j]
         }
      }
   }
   return res
}

堆优化版的Prim算法


// Edge 最小生成树prim算法(寻找已知节点到位置节点的最小路径用堆优化)
//graph 中值为math.MaxInt的值为不可达
type Edge struct {
   startVertex int
   endVertex   int
   weight      int
}
type EdgeHeap []Edge

func (h EdgeHeap) Len() int           { return len(h) }
func (h EdgeHeap) Less(i, j int) bool { return h[i].weight < h[j].weight }
func (h EdgeHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *EdgeHeap) Push(x interface{}) {
   *h = append(*h, x.(Edge))
}
func (h *EdgeHeap) Pop() interface{} {
   n := len(*h)
   res := (*h)[n-1]
   *h = (*h)[:n-1]
   return res
}

func primHeap(graph [][]int, randomVertex int) int {
   //F代表两点之间不可达
   const F = math.MaxInt
   n := len(graph)
   //图中已经遍历到的顶点到未遍历的顶点的最短的距离
   distHeap := make(EdgeHeap, n)
   //图中的顶点是否被访问过
   visit := make([]bool, n)
   //最小生成书的路径和
   res := 0
   //节点访问数
   count := 1

   curIdx := randomVertex

   //标记初始访问节点
   visit[curIdx] = true
   //初始化当前节点到未访问节点的距离
   for i := 0; i < n; i++ {
      if graph[curIdx][i] != F {
         distHeap[i] = Edge{curIdx, i, graph[curIdx][i]}
      }
   }
   heap.Init(&distHeap)
   for len(distHeap) > 0 && count < n {
      edge := heap.Pop(&distHeap).(Edge)
      //两个顶点都已访问过的话,说明如果在加入该条边就构成环，所以跳过
      if visit[edge.startVertex] && visit[edge.endVertex] {
         continue
      }
      if !visit[edge.startVertex] {
         visit[edge.startVertex] = true
         count++
         res += edge.weight
         for i := 0; i < n; i++ {
            if !visit[i] {
               heap.Push(&distHeap, Edge{edge.startVertex, i, graph[edge.startVertex][i]})
            }
         }
      } else {
         count++
         visit[edge.endVertex] = true
         res += edge.weight
         for i := 0; i < n; i++ {
            if !visit[i] {
               heap.Push(&distHeap, Edge{edge.endVertex, i, graph[edge.endVertex][i]})
            }
         }
      }
   }
   return res
}

MST算法之Kruskal

算法参考地址: https://www.geeksforgeeks.org/kruskals-minimum-spanning-tree-algorithm-greedy-algo-2/

前置知识:由于Kruskal使用并查集算法来检测图中是否存在环。因此，我们建议阅读以下文章作为先决条件。联合查找算法|设置 1（检测图形中的周期）并集查找算法|集合 2（按秩和路径压缩并集）

不了解的同学可以也参考:https://blog.csdn.net/the_zed/article/details/105126583,该博主以我们熟悉的故事为主题使我们更加容易的学习和了解并查集算法.

算法的流程

1. 按其权重的非递减顺序对所有边进行排序。 2. 选择最小的边缘。检查它是否与到目前为止形成的生成树形成一个循环。如果未形成循环，则包括此边。否则，丢弃它。 3. 重复步骤#2，直到生成树中有（V-1）条边。

该算法是贪婪算法。贪婪的选择是选择在迄今为止构建的MST中不会导致循环的最小重量边缘。让我们通过一个例子来理解它：考虑下面的输入图。

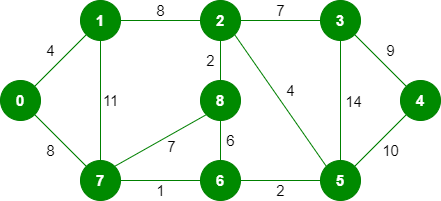
该图包含 9 个顶点和 14 条边。因此，形成的最小生成树将具有（9 – 1）= 8条边。

After sorting:

Weight   Src    Dest
1         7      6
2         8      2
2         6      5
4         0      1
4         2      5
6         8      6
7         2      3
7         7      8
8         0      7
8         1      2
9         3      4
10        5      4
11        1      7
14        3      5

现在，从排序的边列表中逐个选取所有边 1。*选取边 7-6：*未形成循环，请将其包括在内。

2.*拾取边缘8-2：*不形成循环，包括它。

3.*拾取边缘6-5：*不形成循环，包括它。

4.*拾取边缘0-1：*不形成循环，包括它。

5.*拾取边缘2-5：*不形成循环，包括它。

6. 拾取边缘 8-6：由于包含此边缘会导致循环，因此请将其丢弃。 7.*拾取边缘2-3：*不形成循环，包括它。

8. 拾取边缘 7-8：由于包含此边缘会导致循环，因此请将其丢弃。 9.*拾取边缘0-7：*不形成循环，包括它。

10. 选取边缘 1-2：由于包含此边缘会导致循环，因此请将其丢弃。 11.*拾取边缘3-4：*不形成循环，包括它。

由于包含的边数等于（V – 1），因此算法在此处停止。

算法的实现(golang)

type Edge struct {
    startVertex int
    endVertex   int
    weight      int
}
type EdgeHeap []Edge

func (h EdgeHeap) Len() int           { return len(h) }
func (h EdgeHeap) Less(i, j int) bool { return h[i].weight < h[j].weight }
func (h EdgeHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *EdgeHeap) Push(x interface{}) {
    *h = append(*h, x.(Edge))
}
func (h *EdgeHeap) Pop() interface{} {
    n := len(*h)
    res := (*h)[n-1]
    *h = (*h)[:n-1]
    return res
}

//并查集
var tree []int

//初始化并查集
func initTree(n int) {
   tree = make([]int, n)
   for i := 0; i < n; i++ {
      tree[i] = i
   }
}

//返回当前节点的头结点
func search(a int) int {
   if a == tree[a] {
      return a
   } else {
      //压缩路径
      tree[a] = search(tree[a])
      return tree[a]
   }
}

func union(a, b int) {
   rootA := search(a)
   rootB := search(b)
   if rootA == rootB {
      //a和b已经在同一颗树上
      return
   }
   //暂定谁的数值大谁就是老大
   if rootA > rootB {
      tree[rootB] = rootA
   } else {
      tree[rootA] = rootB
   }
}
func Kruskal(graph [][]int) int {
   //F代表两点之间不可达
   const F = math.MaxInt
   n := len(graph)
   initTree(n)
   //图中已经遍历到的顶点到未遍历的顶点的最短的距离
   distHeap := make(EdgeHeap, n)
   //已经遍历的边的数量
   count := 0
   //最小生成书的路径和
   res := 0

   for i := 0; i < n; i++ {
      for j := i + 1; j < n; j++ {
         distHeap = append(distHeap, Edge{i, j, graph[i][j]})
      }
   }
   heap.Init(&distHeap)

   //边的数目为n-1的时候即为最小生成树
   for count < n && len(distHeap) > 0 {
      edge := heap.Pop(&distHeap).(Edge)
      if search(edge.startVertex) != search(edge.endVertex) {
         count++
         union(edge.startVertex, edge.endVertex)
         res += edge.weight
      }
   }
   return res
}

总结

最小生成树(Minimum Spanning Tree)算法在我们的实际中有很多的应用,因此掌握最小生成树算法是非常有必要的,而最小生成树又有两种实现(Prim和Kruskal),这两种算法并没有什么优劣之分,从两种算法的实现可以看出,Prim算法是以顶点为基础,一点一点向外延申,直到所有的顶点都便利完成,算法结束,得到最小生成树,而Kruskal是以边为基础向外扩展,知道有n-1条边,算法结束,得到最小生成树.所以我们可以得到(假如有两棵顶点树相同的树)Prim更适用于边数较多的图(稠密图),而Kruskal更适用于边数较少的图 (稀疏图).