LeetCode 周赛 342(2023/04/23)容斥原理、计数排序、滑动窗口、子数组 GCB
本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。
大家好,我是小彭。
前天刚举办 2023 年力扣杯个人 SOLO 赛,昨天周赛就出了一场 Easy - Easy - Medium - Medium 的水场,不得不说 LeetCode 是懂礼数的 。
接下来,请你跟着小彭的思路,一步步将问题做难,再将问题做简单。
往期回顾:LeetCode 单周赛 341 · 难度上来了,图论的问题好多啊!
LeetCode 周赛 342 概览
Q1. 计算列车到站时间(Easy)
简单模拟题,不多讲解。
Q2. 倍数求和(Easy)
题解 1:暴力解法 $O(n)$ 时间复杂度
题解 2:分析数据特征后发现数据存在等差数列性质,我们利用容斥原理和等差数列求和公式,可以把优化到 $O(1)$ 时间复杂度
Q3. 滑动子数组的美丽值(Medium)
题解 1:在滑动窗口的基础上,结合快速选择查找滑动窗口中第 x 小的元素,时间复杂度是 $O(n·k)$
题解 2:分析数据特征后发现题目的值域非常小,我们可以用计数排序代替快速选择,时间复杂度为 $O(n·U)$
Q4. 使数组所有元素变成 1 的最少操作次数(Medium)
在问题分析后我们将原问题抽象为 “寻找 GCB 为 1 的最短子数组”,关联相似的 “和为 k 的最短子数组” 问题,我们有从暴力 → 有序集合 → 单调性优化的解法:
题解 1:暴力 $O(n·(n + logU))$ 时间复杂度
题解 2:有序集合 $O(n·lgU·lg(lgU))$ 时间复杂度
题解 3:单调性优化 $O(n·lgU)$ 时间复杂度

Q1. 计算列车到站时间(Easy)
题目地址
https://leetcode.cn/problems/calculate-delayed-arrival-time/
题目描述
给你一个正整数 arrivalTime 表示列车正点到站的时间(单位:小时),另给你一个正整数 delayedTime 表示列车延误的小时数。
返回列车实际到站的时间。
注意,该问题中的时间采用 24 小时制。
示例 1:
输入:arrivalTime = 15, delayedTime = 5
输出:20
解释:列车正点到站时间是 15:00 ,延误 5 小时,所以列车实际到站的时间是 15 + 5 = 20(20:00)。
示例 2:
输入:arrivalTime = 13, delayedTime = 11
输出:0
解释:列车正点到站时间是 13:00 ,延误 11 小时,所以列车实际到站的时间是 13 + 11 = 24(在 24 小时制中表示为 00:00 ,所以返回 0)。
提示:
1 <= arrivaltime < 241 <= delayedTime <= 24
题解(模拟)
简单模拟题,按题意实现即可。
class Solution {
fun findDelayedArrivalTime(arrivalTime: Int, delayedTime: Int): Int {
return (arrivalTime + delayedTime) % 24
}
}
复杂度分析:
- 时间复杂度:$O(1)$
- 空间复杂度:$O(1)$
Q2. 倍数求和(Easy)
题目地址
https://leetcode.cn/problems/sum-multiples/
题目描述
给你一个正整数 n ,请你计算在 [1,n] 范围内能被 3、5、7 整除的所有整数之和。
返回一个整数,用于表示给定范围内所有满足约束条件的数字之和。
示例 1:
输入:n = 7
输出:21
解释:在[1, 7] 范围内能被 3、5、7 整除的所有整数分别是 3、5、6、7 。数字之和为21 。
示例 2:
输入:n = 10
输出:40
解释:在[1, 10] 范围内能被 3、5、7 整除的所有整数分别是 3、5、6、7、9、10 。数字之和为40 。
示例 3:
输入:n = 9
输出:30
解释:在[1, 9] 范围内能被 3、5、7 整除的所有整数分别是 3、5、6、7、9 。数字之和为30 。
提示:
1 <= n <= 103
预备知识 - 容斥原理
定义集合 A 表示能够被 3 整除的数,定义集合 B 表示能够被 5 整除的数,定义集合 C 表示能够被 7 整除的数。如果把这 3 个集合直接加起来,会多出来一些元素重复统计了,因此需要扣除 A ∩ B,A ∩ C 和 B ∩ C ,但是又有一小部分元素多扣了,反而再需要加上 A ∩ B ∩ C。这就是 容斥原理:
$$
A ∪ B ∪ C = A + B + C - A ∩ B - A ∩ C - B ∩ C + A ∩ B ∩ C
$$
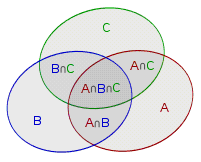
其中:
- A ∪ B ∪ C 表示能够被 3 或 5 或 7 整除的数,也就是原问题的解;
- A ∩ B 表示能够同时被 3 和 5 整除的数;
- A ∩ C 表示能够同时被 3 和 7 整除的数;
- B ∩ C 表示能够同时被 5 和 7 整除的数。
预备知识 - 等差数列求和
- 等差数列求和公式:(首项 + 尾项) * 项数 / 2
题解一(暴力)
先思考暴力解法:
算法:枚举每个数,检查该数字是否为 3 / 5 / 7 的倍数,是则计入结果中。
class Solution {
fun sumOfMultiples(n: Int): Int {
var ret = 0
for (i in 1 .. n) {
if(i % 3 == 0 || i % 5 == 0 || i % 7 == 0) ret += i
}
return ret
}
}
复杂度分析:
- 时间复杂度:$O(n)$ 其中 n 为 nums 数组的长度,每个元素最多访问 1 次;
- 空间复杂度:$O(1)$
题解二(容斥原理 + 等差数列求和公式)
暴力解法是否有优化空间呢,先分析重复计算:
- 要点 1:可以观察到 [1, n] 范围中的目标数是存在关联的,以 3 的倍数为例,3、6、9、12 是以 3 为等差的等差数列,而等差数列的和可以使用公式计算。数字 m 在 [1, n] 范围内中的倍数为 n / m 个,可以使用等差数列求和公式以 O(1) 算出这部分元素之和;
- 要点 2:结合容斥原理,可以在 O(1) 时间复杂度求出原问题。那么能够同时被 3 和 5 整除的等差数列如何计算呢?其实就是计算 15 的倍数。同理能够同时被 3 和 5 和 7 整除的等差数列就是 105 的倍数。
至此,结合容斥原理模拟即可:
class Solution {
fun sumOfMultiples(n: Int): Int {
return sum(n, 3) + sum(n, 5) + sum(n, 7) - sum(n, 15) - sum(n, 21) - sum(n, 35) + sum(n, 105)
}
private fun sum(n:Int, k:Int) :Int {
// 等差数列求和公式:(首项 + 尾项) * 项数 / 2
return (k + (n / k * k)) * (n / k) / 2
}
}
复杂度分析:
- 时间复杂度:$O(1)$
- 空间复杂度:$O(1)$
Q3. 滑动子数组的美丽值(Medium)
题目地址
https://leetcode.cn/problems/sliding-subarray-beauty/description/
题目描述
给你一个长度为 n 的整数数组 nums ,请你求出每个长度为 k 的子数组的 美丽值 。
一个子数组的 美丽值 定义为:如果子数组中第 x 小整数 是 负数 ,那么美丽值为第 x 小的数,否则美丽值为 0 。
请你返回一个包含 n - k + 1 个整数的数组,依次** 表示数组中从第一个下标开始,每个长度为 k 的子数组的 美丽值 。
- 子数组指的是数组中一段连续 非空 的元素序列。
示例 1:
输入:nums = [1,-1,-3,-2,3], k = 3, x = 2
输出:[-1,-2,-2]
解释:总共有 3 个 k = 3 的子数组。
第一个子数组是[1, -1, -3] ,第二小的数是负数 -1 。
第二个子数组是[-1, -3, -2] ,第二小的数是负数 -2 。
第三个子数组是[-3, -2, 3] ,第二小的数是负数 -2 。
示例 2:
输入:nums = [-1,-2,-3,-4,-5], k = 2, x = 2
输出:[-1,-2,-3,-4]
解释:总共有 4 个 k = 2 的子数组。
[-1, -2] 中第二小的数是负数 -1 。[-2, -3] 中第二小的数是负数 -2 。[-3, -4] 中第二小的数是负数 -3 。[-4, -5] 中第二小的数是负数 -4 。
示例 3:
输入:nums = [-3,1,2,-3,0,-3], k = 2, x = 1
输出:[-3,0,-3,-3,-3]
解释:总共有 5 个 k = 2 的子数组。
[-3, 1] 中最小的数是负数 -3 。[1, 2] 中最小的数不是负数,所以美丽值为 0 。[2, -3] 中最小的数是负数 -3 。[-3, 0] 中最小的数是负数 -3 。[0, -3] 中最小的数是负数 -3 。
提示:
n == nums.length1 <= n <= 1051 <= k <= n1 <= x <= k50 <= nums[i] <= 50
预备知识
求出每个长度为 k 的子数组的美丽值,容易想到可以用滑动窗口。
伪代码为:
// 伪代码
for (i in 0 until n) {
// 进入窗口
list.add(i)
// 离开窗口
if (i >= k) list.remove(i - k)
if (i >= k - 1) {
// 计算窗口答案
}
}
题解一(滑动窗口 + 快速选择 · 超出时间限制)
在滑动窗口的基础上,使用快速选择查找窗口中第 x 小的数:
class Solution {
private val random = Random(0)
fun getSubarrayBeauty(nums: IntArray, k: Int, x: Int): IntArray {
val n = nums.size
val ret = LinkedList<Int>()
val list = ArrayList<Int>()
for (i in 0 until n) {
// 进入窗口
list.add(i)
// 离开窗口
if (i >= k) list.remove(i - k)
if (i >= k - 1) {
// 计算窗口答案
quickSelect(nums, list, x)
val num = nums[list[x - 1]]
ret.add(if (num < 0) num else 0)
}
}
return ret.toIntArray()
}
private fun quickSelect(nums: IntArray, list: ArrayList<Int>, x: Int) {
val target = x - 1
var left = 0
var right = list.size - 1
while (left < right) {
val pivot = partition(nums, list, left, right)
if (pivot == target) {
return
} else if (pivot < target) {
left = pivot + 1
} else {
right = pivot - 1
}
}
}
private fun partition(nums: IntArray, list: ArrayList<Int>, left: Int, right: Int): Int {
val random = random.nextInt(right - left + 1) + left
list.swap(random, right)
var p = left
for (i in left until right) {
if (nums[list[i]] < nums[list[right]]) list.swap(i, p++)
}
list.swap(p, right)
return p
}
private fun ArrayList<Int>.swap(i: Int, j: Int) {
val temp = this[i]
this[i] = this[j]
this[j] = temp
}
}
复杂度分析:
- 时间复杂度:$O(n·k)$ 其中 n 是 nums 数组的长度,单次窗口快速选择的时间复杂度是 $O(k)$;
- 空间复杂度:$O(k)$ 滑动窗口空间。
题解二(滑动窗口 + 计数排序)
注意到题目的值域非常小,能否利用起来:
我们可以用计数排序代替快速选择,用 cnts 计数数组计算窗口内每个元素的出现次数,再根据计数数组计算出第 x 小的数:
class Solution {
private val random = Random(0)
fun getSubarrayBeauty(nums: IntArray, k: Int, x: Int): IntArray {
val n = nums.size
val OFFSET = 50
val cnts = IntArray(OFFSET * 2 + 1)
val ret = IntArray(n - k + 1)
outer@ for (i in 0 until n) {
// 进入窗口
cnts[OFFSET + nums[i]]++
// 离开窗口
if (i >= k) cnts[OFFSET + nums[i - k]]--
if (i >= k - 1) {
// 计算窗口美丽值
var count = x
// for (num in -OFFSET .. -1) {
for (num in -OFFSET .. OFFSET) {
count -= cnts[num + 50]
if (count <= 0) {
// 找到第 x 小的数
// ret[i - k + 1] = num
ret[i - k + 1] = if(num < 0) num else 0
continue@outer
}
}
}
}
return ret
}
}
另外,由于题目要求美丽值是负数,所以在计算窗口美丽值时,我们只需要枚举 [-50, -1] 的元素值。
复杂度分析:
- 时间复杂度:$O(n·U)$ 其中 n 是 nums 数组的长度,U 是值域大小 101。每次滑动窗口求第 x 小的元素时间是 $O(U)$;
- 空间复杂度:$O(U)$ 计数数组空间。
Q4. 使数组所有元素变成 1 的最少操作次数(Medium)
题目地址
题目描述
给你一个下标从 0 开始的 正 整数数组 nums 。你可以对数组执行以下操作 任意 次:
- 选择一个满足
0 <= i < n - 1的下标i,将nums[i]或者nums[i+1]两者之一替换成它们的最大公约数。
请你返回使数组 nums 中所有元素都等于 1 的 最少 操作次数。如果无法让数组全部变成 1 ,请你返回 -1 。
两个正整数的最大公约数指的是能整除这两个数的最大正整数。
示例 1:
输入:nums = [2,6,3,4]
输出:4
解释:我们可以执行以下操作:
- 选择下标 i = 2 ,将 nums[2] 替换为 gcd(3,4) = 1 ,得到 nums = [2,6,1,4] 。
- 选择下标 i = 1 ,将 nums[1] 替换为 gcd(6,1) = 1 ,得到 nums = [2,1,1,4] 。
- 选择下标 i = 0 ,将 nums[0] 替换为 gcd(2,1) = 1 ,得到 nums = [1,1,1,4] 。
- 选择下标 i = 2 ,将 nums[3] 替换为 gcd(1,4) = 1 ,得到 nums = [1,1,1,1] 。
示例 2:
输入:nums = [2,10,6,14]
输出:-1
解释:无法将所有元素都变成 1 。
提示:
2 <= nums.length <= 501 <= nums[i] <= 106
问题分析
分析目标结果:
使得数组中所有元素都变成 1 的最少操作次数。
分析题目示例:
- 由于在每次操作中最多只能将一个数字修改为最大公约数,那么将 1 个元素操作为 “1” 的最小操作次数(如果可行)不会低于 1 次,将 n 个大于 1 的元素操作为 “1” 的最小次数不会低于 n 次,例如样例 [2,6,1,4]。
- 如果数组中至少存在 1 个 “1” 时,我们只需要将每个 “1” 与相邻的 “非 1” 元素组合操作,就能将所有元素,例如样例 [2,6,1,4]。这说明,问题的最小操作次数正好就是数组中不是 “1” 的个数。
- 如果数组中不存在 “1”,需要先操作出原始的 “1”:
- 如果数组中所有元素的最大公约数大于 1,那么无论如何也无法操作出数字 1,例如样例 [2, 10, 6, 14];
- 否则,我们总可以操作 x 次获得原始 “1”,那么问题就等于 count + n - 1;
至此,程序整体框架确定。伪代码为:
if (所有元素的最大公约数 > 1) return -1
if (1 的个数 > 0) return n - (1 的个数)
操作 count 次得到原始的 “1”
return count + n - 1
接下来,我们需要思考如何计算出操作出原始 “1” 的最小次数:
回归到原问题操作,我们在每次操作中可以将一个数修改为最大公约数,那么对于连续的一段子数组(长度为 subSize),我们总可以用 subSize - 1 次操作将其中一个数变为整个子数组的最大公约数。如果这个最大公约数是 1,那么操作次数正好是 subSize - 1,反之无法操作出 1。
至此,可以想出暴力解法:
题解一(暴力枚举子数组)
在暴力解法中,我们枚举所有子数组,记录出所有子数组操作出原始 “1” 的最少操作次数。
class Solution {
fun minOperations(nums: IntArray): Int {
val n = nums.size
// 1 的个数
var cnt1 = 0
var gcbAll = 0
for (x in nums) {
gcbAll = gcb(gcbAll, x)
if (x == 1) cnt1++
}
// 所有数的最大公约数大于 1
if (gcbAll > 1) return -1
// 1 的个数大于 0
if (cnt1 > 0) return n - cnt1
// 操作出原始 “1” 的最小次数
var minCount = n
// 枚举子数组
for (i in 0 until n) {
var gcb = 0
for (j in i until n) {
gcb = gcb(gcb, nums[j])
if (gcb == 1) {
minCount = Math.min(minCount, j - i /* 子数组长度 - 1 */)
break // 继续枚举 i 为起点的子数组不会得到更优解
}
}
}
return minCount + n - 1
}
// 求 x 和 y 的最大公约数(辗转相除法)
private fun gcb(x: Int, y: Int): Int {
var a = x
var b = y
while (b != 0) {
val temp = a % b
a = b
b = temp
}
return a
}
}
复杂度分析:
- 时间复杂度:$O(n·(n + logU))$ 其中 n 是 nums 数组的长度,U 是数组元素的最大值。单次 GCD 计算的时间复杂度是 $O(logU)$,乍看起来算法整体的时间复杂度是 $O(n^2·logU)$,其实不对。因为在每层循环中,每次 GCD 计算并不是独立的,而是贯穿整个内层循环的,所以 GCD 的总时间取决于数据的最大值 U,在辗转相除中取余的次数也取决于 U。
- 空间复杂度:$O(1)$ 不考虑结果数组,仅使用常量级别空间。
题解一的复杂度是平方级别的,如果放大题目数据量到 10^5 要怎么做?
问题抽象
在分析暴力解法的重复计算之前,我先向你抛出一个 “题外话”:
请你回答:“给定一个整数数组 nums 和目标和 k,如何求和为 k 的最短子数组?”
- 解法 1:暴力枚举所有子数组,记录出所有子数组和为 k 的最短子数组长度(这与题解一暴力枚举子数组求操作出原始 “1” 的最少操作次数类似);
- 解法 2:我们从左向右线性遍历,并维护以 num[j] 为右端点的前缀和映射表 。在此基础上,我们将当前位置 nums[i] 的前缀和与前缀和映射表中的每个元素取差值,就可以快速地获得以 num[i] 为右端点所有子数组的和。另外,由于我们是从左向右遍历的,所以前缀和映射表记录的索引正好是可以构造最短子数组的索引,子数组长度为 i - j + 1(当然,我们可以直接 O(1) 查询目标前缀和出现时的索引,而不需要真的用前缀和映射表的每个元素取差值)。
注:这个 “题外话” 与 LeetCode 560. 和为 K 的子数组 类似,如果你不熟悉可以先做做看。
那么,这个 “题外话” 与今天这道题有什么关系:
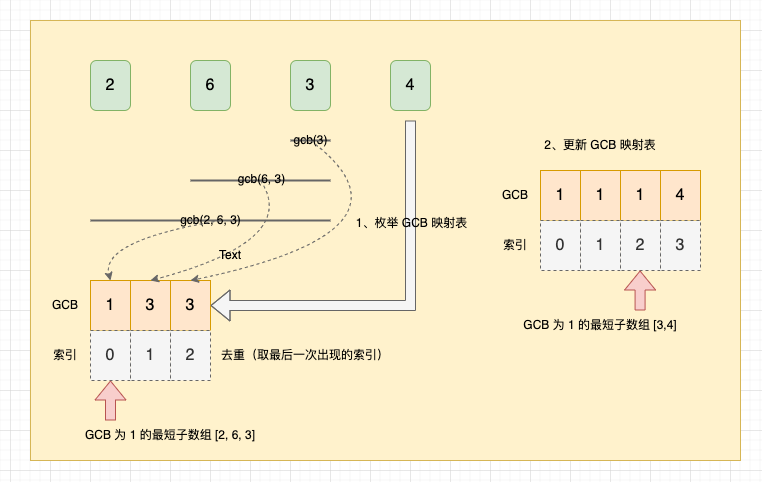
根据 GCB 运算的性质,当我们以 nums[i] 为左端点,不断向右扩展子数组的右端点时,我们的目标是求 “GCB 为 1 的子数组” 对吧。与 “求和为 k 的最短子数组” 类似,我们可以维护以 nums[j] 为左端点的 GCB 映射表 <gcb to 左端点 index>。在此基础上,我们将当前位置 nums[i] 与 GCB 映射表中的每个元素取 GCB,就可以快速的获得以 nums[i] 为右端点的所有子数组的 GCB。
那听起来这个算法依然是 O(n^2)?不对。
原因在题解一的时间复杂度分析中讲到了,因为每次 GCD 计算并不是独立的,而是贯穿整个循环的,GCB 映射表的大小取决于数据的最大值 U,而不是数据量,最多有 logU 种 GCB。因此优化后算法的时间复杂度是 O(n·lgU),但增加了空间复杂度为 O(lgU)。
示意图
题解二(有序集合)
至此,在题解一的基础上修改 “枚举子数组计算操作出原始 “1” 的最小次数” 不分代码即可:
class Solution {
fun minOperations(nums: IntArray): Int {
// 略...
// 计算操作出原始 “1” 的最小次数
var minCount = n
// gcb 散列表 <gcd to 左端点 index>
var gcbMap = TreeMap<Int, Int>()
// 枚举子数组
for (i in 0 until n) {
val newGcbMap = TreeMap<Int, Int>()
// 枚举 gcb 映射表
for ((gcb, index) in gcbMap) {
newGcbMap[gcb(gcb, nums[i])] = index
}
newGcbMap[nums[i]] = i
// 检查最小的 gcb 是否为 1
val minEntry = newGcbMap.firstEntry()
if (1 == minEntry.key) {
minCount = Math.min(minCount, i - minEntry.value /* 子数组长度 - 1 */)
}
gcbMap = newGcbMap
}
return minCount + n - 1
}
// 求 x 和 y 的最大公约数
private fun gcb(x: Int, y: Int): Int {
// 略...
}
}
复杂度分析:
- 时间复杂度:$O(n·lgU·lg(lgU))$ 由于使用了有序集合,所以每一轮迭代中要算上排序时间 $O(lgU·lg(lgU))$;
- 空间复杂度:$O(lgU)$ GCB 映射表空间。
题解三(单调性优化)
思路参考:灵茶山艾府的题解
题解二的时间复杂度比我们分析的复杂度略要一些,如何寻找优化空间?
继续分析 GCB 的数据特征,可以发现:当我们从左向右遍历时,随着子数组的长度增大,子数组的 GCB 要么不变,要么变小,存在 单调性。 所以,我们并不需要维护有序集合,GCB 列表中最靠前的元素一定是最小的 GCB。
class Solution {
fun minOperations(nums: IntArray): Int {
// 略...
// 计算操作出原始 “1” 的最小次数
var minCount = n
// gcb 列表 <gcd to 左端点 index>
var gcbs = ArrayList<IntArray>()
// 枚举子数组
for (i in 0 until n) {
val newGcbs = ArrayList<IntArray>()
// 枚举 gcb 列表
for (element in gcbs) {
val gcb = gcb(element[0], nums[i])
if (newGcbs.isEmpty() || newGcbs[newGcbs.size - 1][0] != gcb) {
// 增加 GCB
newGcbs.add(intArrayOf(gcb, element[1]))
} else {
// 原地去重
newGcbs[newGcbs.size - 1][1] = element[1]
}
}
newGcbs.add(intArrayOf(nums[i], i))
// 检查最小的 gcb 是否为 1
val minEntry = newGcbs[0]
if (1 == minEntry[0]) {
minCount = Math.min(minCount, i - minEntry[1] /* 子数组长度 - 1 */)
}
gcbs = newGcbs
}
return minCount + n - 1
}
// 求 x 和 y 的最大公约数
private fun gcb(x: Int, y: Int): Int {
// 略...
}
}
复杂度分析:
- 时间复杂度:$O(n·lgU)$
- 空间复杂度:$O(lgU)$
相似题目:
LeetCode 周赛 342(2023/04/23)容斥原理、计数排序、滑动窗口、子数组 GCB的更多相关文章
- Java实现 LeetCode 757 设置交集大小至少为2(排序+滑动窗口)
757. 设置交集大小至少为2 一个整数区间 [a, b] ( a < b ) 代表着从 a 到 b 的所有连续整数,包括 a 和 b. 给你一组整数区间intervals,请找到一个最小的集合 ...
- [LeetCode]3. 无重复字符的最长子串(滑动窗口)
题目 给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度. 示例 1: 输入: "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc ...
- 算法-java代码实现计数排序
计数排序 第10节 计数排序练习题 对于一个int数组,请编写一个计数排序算法,对数组元素排序. 给定一个int数组A及数组的大小n,请返回排序后的数组. 测试样例: [1,2,3,5,2,3], ...
- counting sort 计数排序
//counting sort 计数排序 //参考算法导论8.2节 #include<cstdio> #include<cstring> #include<algorit ...
- 第2章 排序 | 第10节 计数排序练习题 && 基数排序
对于一个int数组,请编写一个计数排序算法,对数组元素排序. 给定一个int数组A及数组的大小n,请返回排序后的数组. 测试样例: [1,2,3,5,2,3],6 [1,2,2,3,3,5] 计数排序 ...
- 【leetcode】239. 滑动窗口最大值
目录 题目 题解 三种解法 "单调队列"解法 新增.获取最大值 删除 代码 题目 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧.你只可以 ...
- 【Leetcode周赛】从contest-111开始。(一般是10个contest写一篇文章)
Contest 111 (题号941-944)(2019年1月19日,补充题解,主要是943题) 链接:https://leetcode.com/contest/weekly-contest-111 ...
- http://www.cnblogs.com/peida/archive/2013/04/23/3036035.html
http://www.cnblogs.com/peida/archive/2013/04/23/3036035.html
- LeetCode 第 342 题(Power of Four)
LeetCode 第 342 题(Power of Four) Given an integer (signed 32 bits), write a function to check whether ...
- LeetCode 第 342 题(Power of Four)
LeetCode 第 342 题(Power of Four) Given an integer (signed 32 bits), write a function to check whether ...
随机推荐
- Android 自定义View (二)
一.前言 上节 通过一个简单的旋转环对自定义view作了一个基本的认识,本文将大致讲解下实现的思路以及对该view的一些可能的改进. 二.思路 主要通过重写 view 中的 onDraw() 方法,利 ...
- nacos启停脚本
nacosServer.sh #!/bin/bash #auther by wangxp PWD=`pwd` #配置java环境变量 JAVA_HOME=/u01/java_home/jdk1.8.0 ...
- shell命令查找文件
1.find命令的参数下面是find命令一些常用参数的例子,有用到的时候查查就行了,像上面前几个贴子,都用到了其中的的一些参数,也可以用man或查看论坛里其它贴子有find命令手册使用name选项文件 ...
- C# DataGridView 新增列 新增行 操作函数 - [ 自律相互分享,共促一起进步 - 社会的正常运维就这么简单,何以权,何以钱...- 张光荣2010年谈社会改正提出的正能量]
功能: 一.列相关: 1.追加列,左插列,右插列, 2.删除列 二.行相关: 1.追加行,上插行,下插行 2.删除行,删除所有空行,清空所有数据... 原理:根据对鼠标于 DataGridView 点 ...
- @DeclareParents声明对象的AOP
今天在使用@DeclareParents时,使用AspectJ拓展对象的接口 public interface Encoreable { void nextPerformance(); } @Comp ...
- nohup /root/runoob.sh > runoob.log 2>&1 &
nohup /root/runoob.sh > runoob.log 2>&1 &****
- C++ || 求一个数中1的位数
点击查看代码 #include<iostream> using namespace std; int f(int x) { int count = 0; while(x) { if (x ...
- Ubuntu解决无法远程连接
检查SSH是否安装 ssh localhost 如果没有安装,通过APT的命令安装 sudo apt install openssh-server 无法连接Ubuntu中的root用户 其他用户可以连 ...
- Python ssh远程登录设备执行命令
# -*-encoding:utf-8 -*- """ @Time : 2022/12/30 10:10 @Auth : ruqing @File :ssh_sonic. ...
- uni-app使用Sqlite
step2:封装常用操作(未对事务进行封装 HTML5+ API Reference (html5plus.org)) // //打开数据库 function openDb(name,path) { ...
