斯坦福NLP课程 | 第1讲 - NLP介绍与词向量初步

作者：韩信子@ShowMeAI，路遥@ShowMeAI，奇异果@ShowMeAI

教程地址：http://www.showmeai.tech/tutorials/36

本文地址：http://www.showmeai.tech/article-detail/231

声明：版权所有，转载请联系平台与作者并注明出处

收藏ShowMeAI查看更多精彩内容

---

ShowMeAI为斯坦福CS224n《自然语言处理与深度学习(Natural Language Processing with Deep Learning)》课程的全部课件，做了中文翻译和注释，并制作成了GIF动图！

本讲内容的深度总结教程可以在这里 查看。视频和课件等资料的获取方式见文末。

引言

CS224n是顶级院校斯坦福出品的深度学习与自然语言处理方向专业课程。核心内容覆盖RNN、LSTM、CNN、transformer、bert、问答、摘要、文本生成、语言模型、阅读理解等前沿内容。

ShowMeAI将从本节开始，依托cs224n课程为主框架，逐篇为大家梳理NLP的核心重点知识原理。

本篇内容覆盖：

第1课直接切入语言和词向量，讲解了自然语言处理的基本概念，文本表征的方法和演进，包括word2vec等核心方法，词向量的应用等。

• 自然语言与文字
• word2vec介绍
• word2vec目标函数与梯度
• 算法优化基础
• word2vec构建的词向量模式

1. 自然语言与词汇含义

1.1 人类的语言与词汇含义

咱们先来看看人类的高级语言。

人类之所以比类人猿更“聪明”，是因为我们有语言，因此是一个人机网络，其中人类语言作为网络语言。人类语言具有信息功能和社会功能。

据估计，人类语言只有大约5000年的短暂历史。语言和写作是让人类变得强大的原因之一。它使知识能够在空间上传送到世界各地，并在时间上传送。

但是，相较于如今的互联网的传播速度而言，人类语言是一种缓慢的语言。然而，只需人类语言形式的几百位信息，就可以构建整个视觉场景。这就是自然语言如此迷人的原因。

1.2 我们如何表达一个词的意思？

我们如何表达一个词的含义呢？有如下一些方式：

• 用一个词、词组等表示的概念。
• 一个人想用语言、符号等来表达的想法。
• 表达在作品、艺术等方面的思想。

理解意义的最普遍的语言方式(linguistic way)：语言符号与语言意义（想法、事情）的相互对应

• denotational semantics：语义

\[signifier(symbol) \Leftrightarrow signified(idea \quad or \quad thing)
\]

1.3 如何在计算机里表达词的意义

要使用计算机处理文本词汇，一种处理方式是WordNet：即构建一个包含同义词集和上位词(“is a”关系)的列表的辞典。

英文当中确实有这样一个wordnet，我们在安装完NLTK工具库和下载数据包后可以使用，对应的python代码如下：

from nltk.corpus import wordnet as wn
poses = { 'n':'noun', 'v':'verb', 's':'adj (s)', 'a':'adj', 'r':'adv'}
for synset in wn.synsets("good"):
        print("{}: {}".format(poses[synset.pos()], ", ".join([l.name() for l in synset.lemmas()])))

from nltk.corpus import wordnet as wn
panda = wn.synset("panda.n.01")
hyper = lambda s: s.hypernyms()
list(panda.closure(hyper))

结果如下图所示：

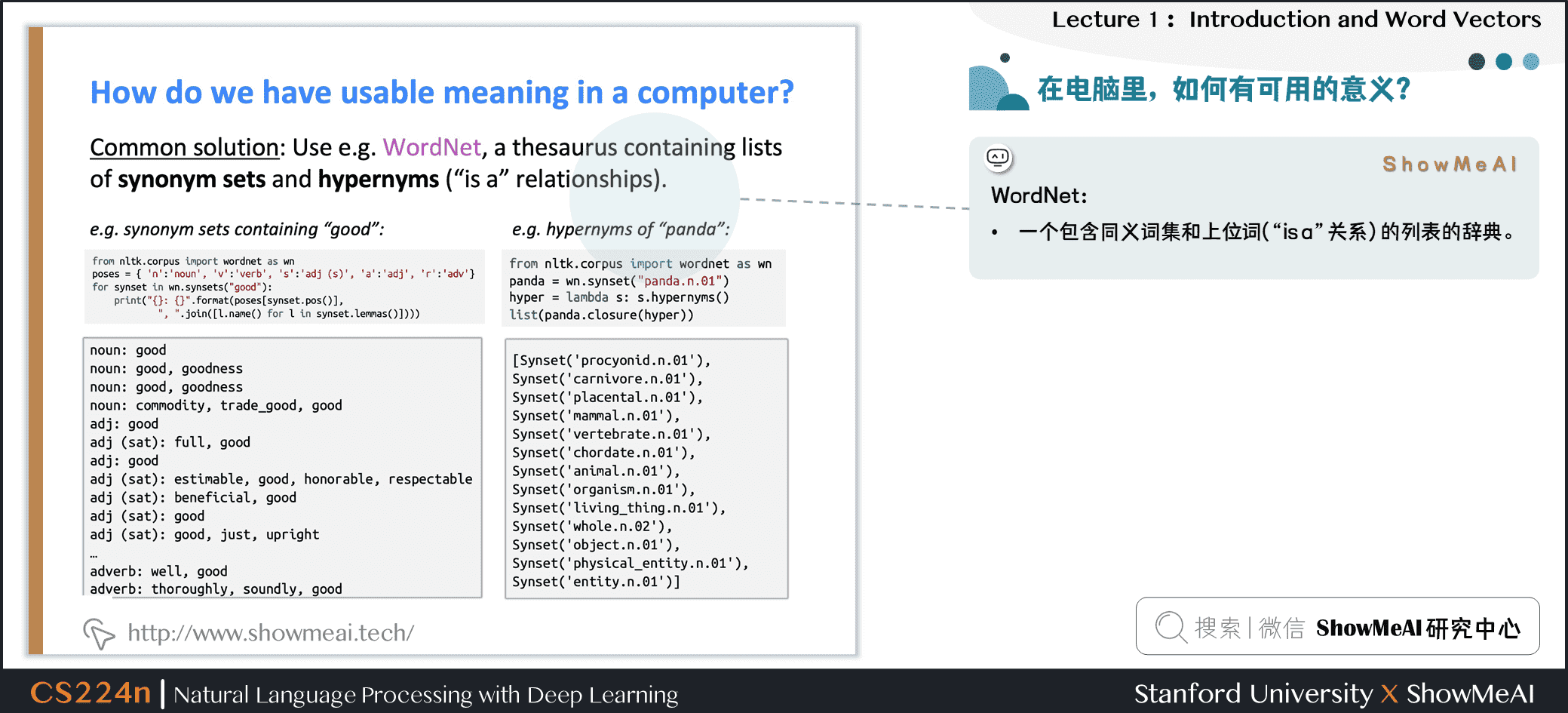
1.4 WordNet的问题

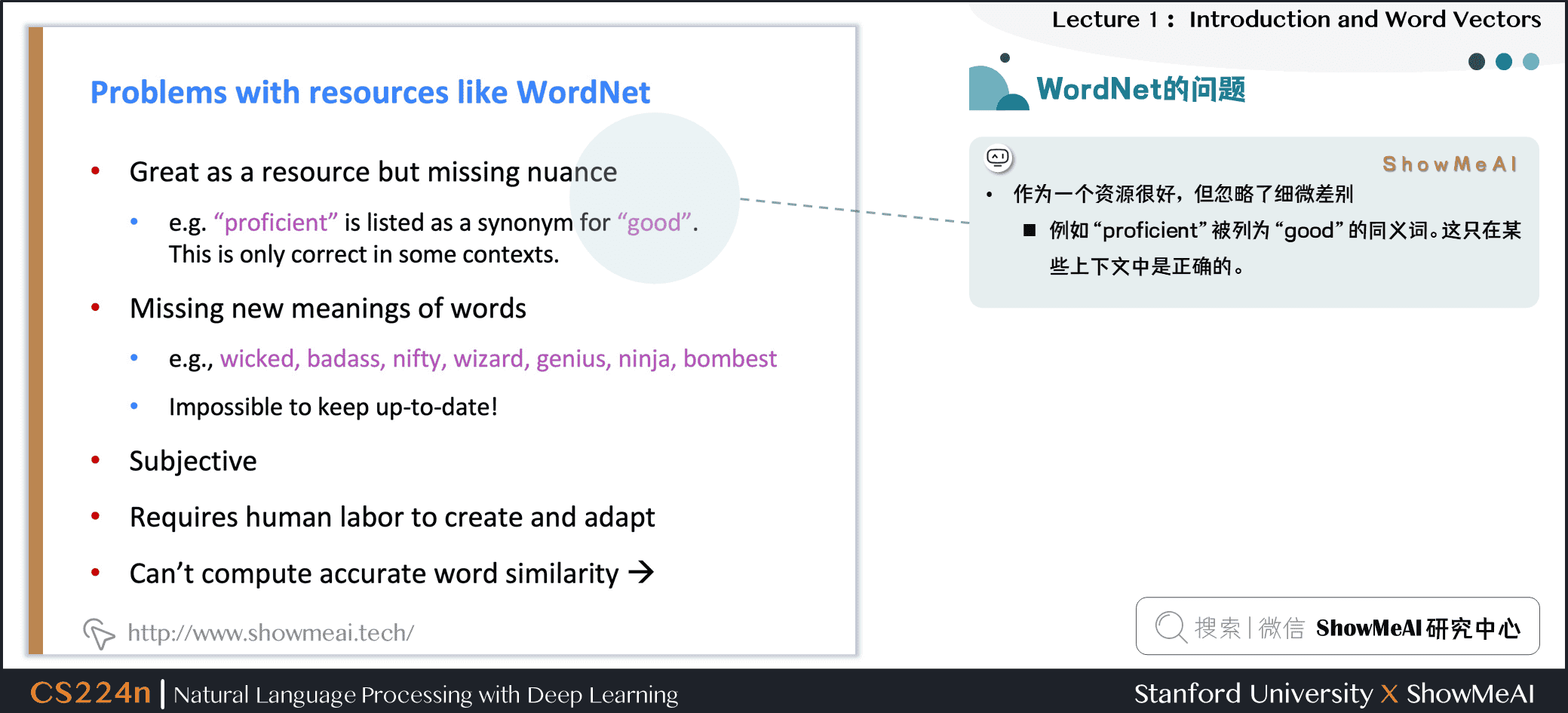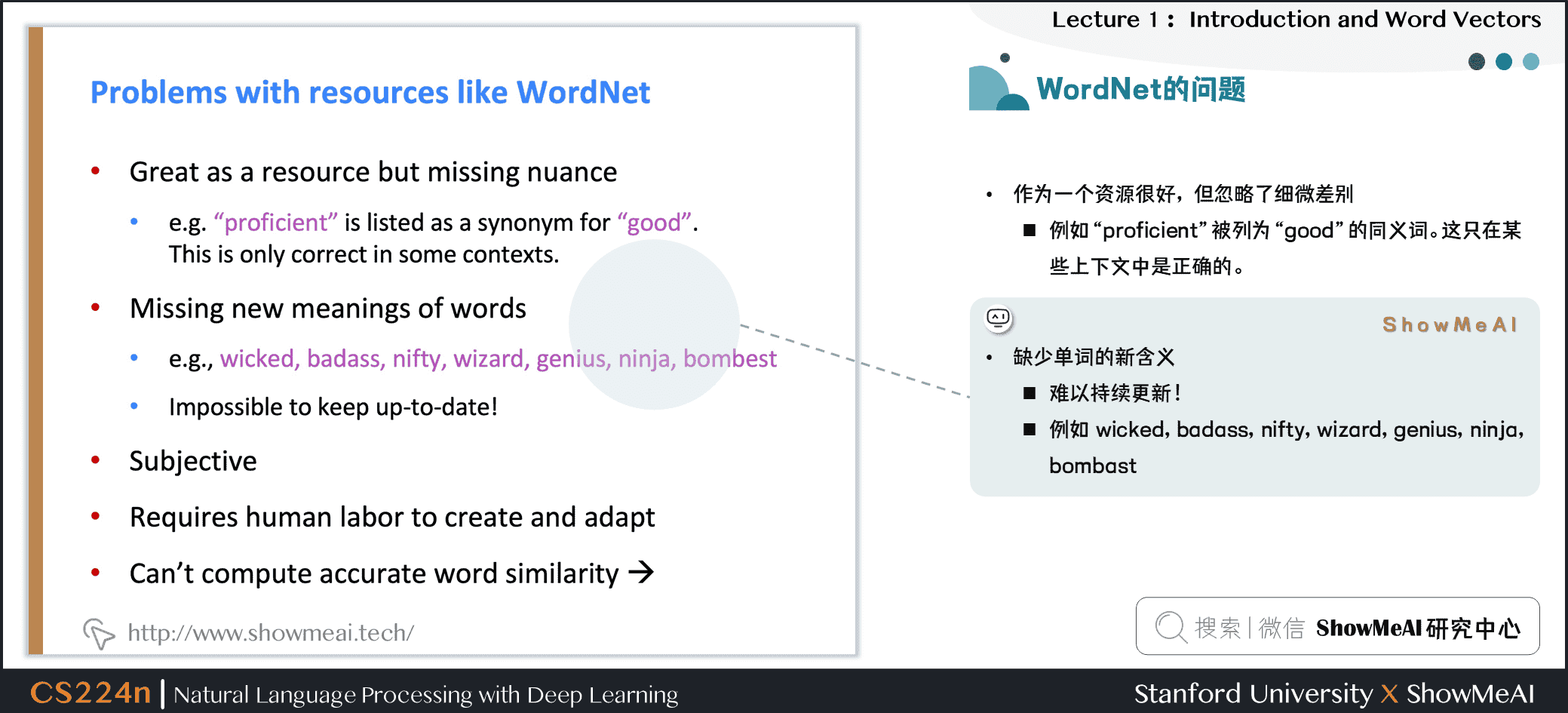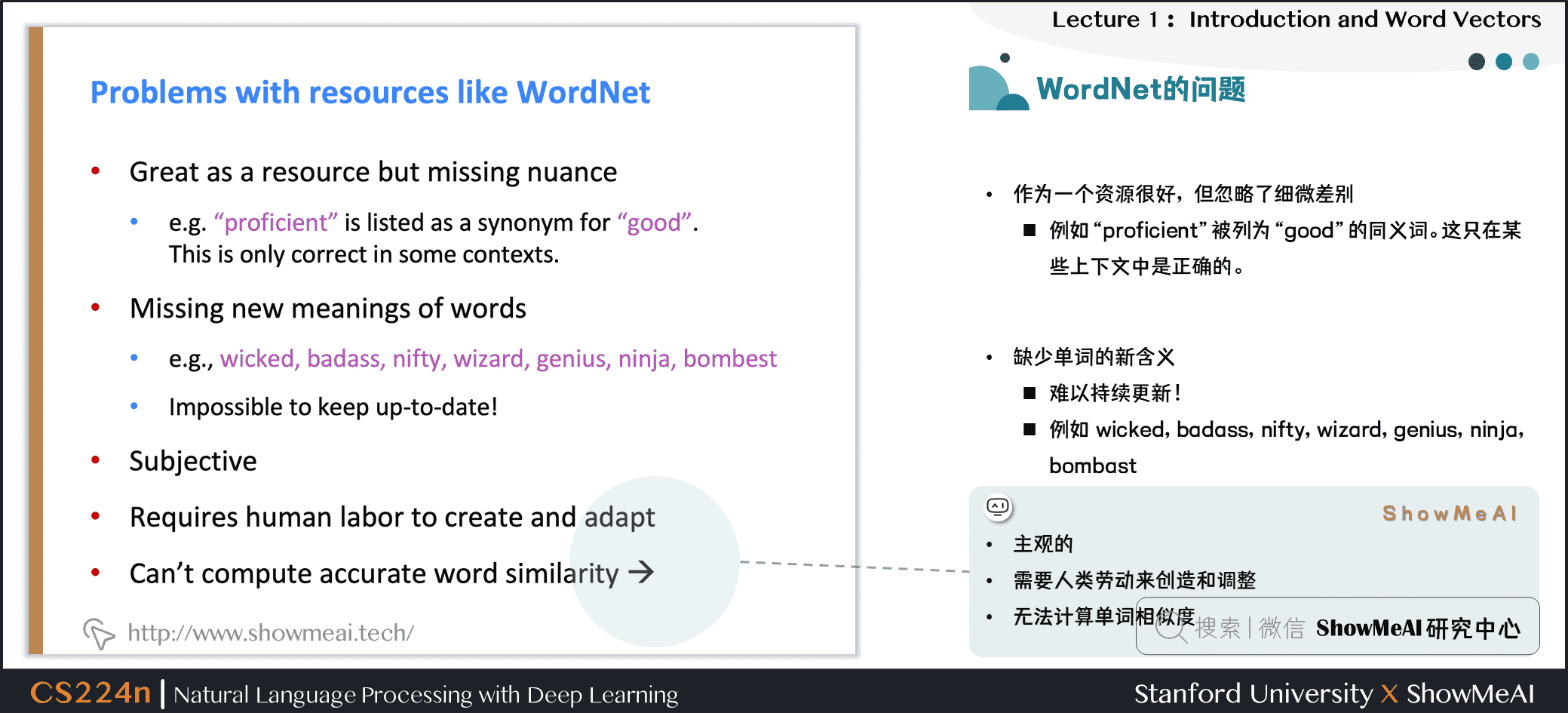
WordNet大家可以视作1个专家经验总结出来的词汇表，但它存在一些问题：

① 忽略了词汇的细微差别

• 例如“proficient”被列为“good”的同义词。这只在某些上下文中是正确的。

② 缺少单词的新含义

• 难以持续更新！
• 例如：wicked、badass、nifty、wizard、genius、ninja、bombast

③ 因为是小部分专家构建的，有一定的主观性

④ 构建与调整都需要很多的人力成本

⑤ 无法定量计算出单词相似度

1.5 文本(词汇)的离散表征

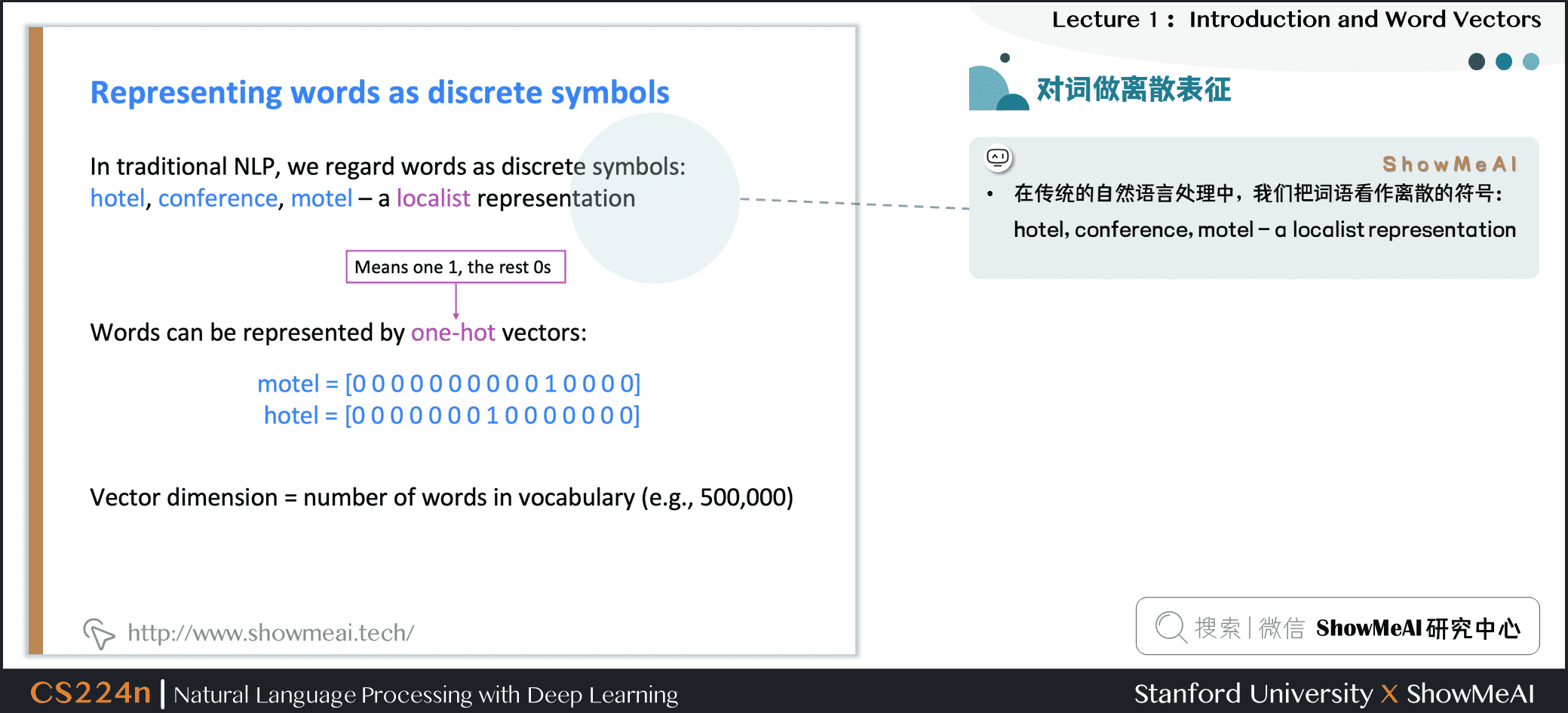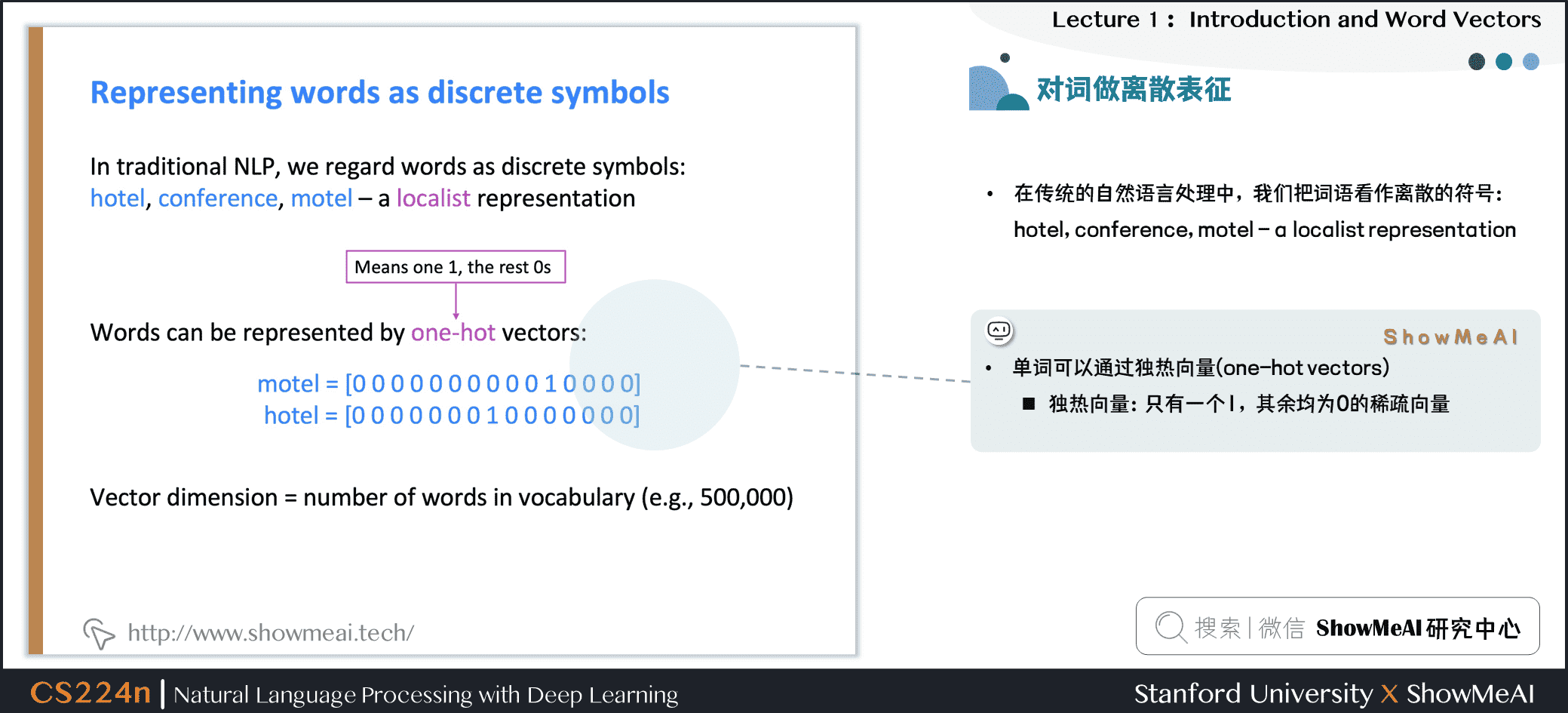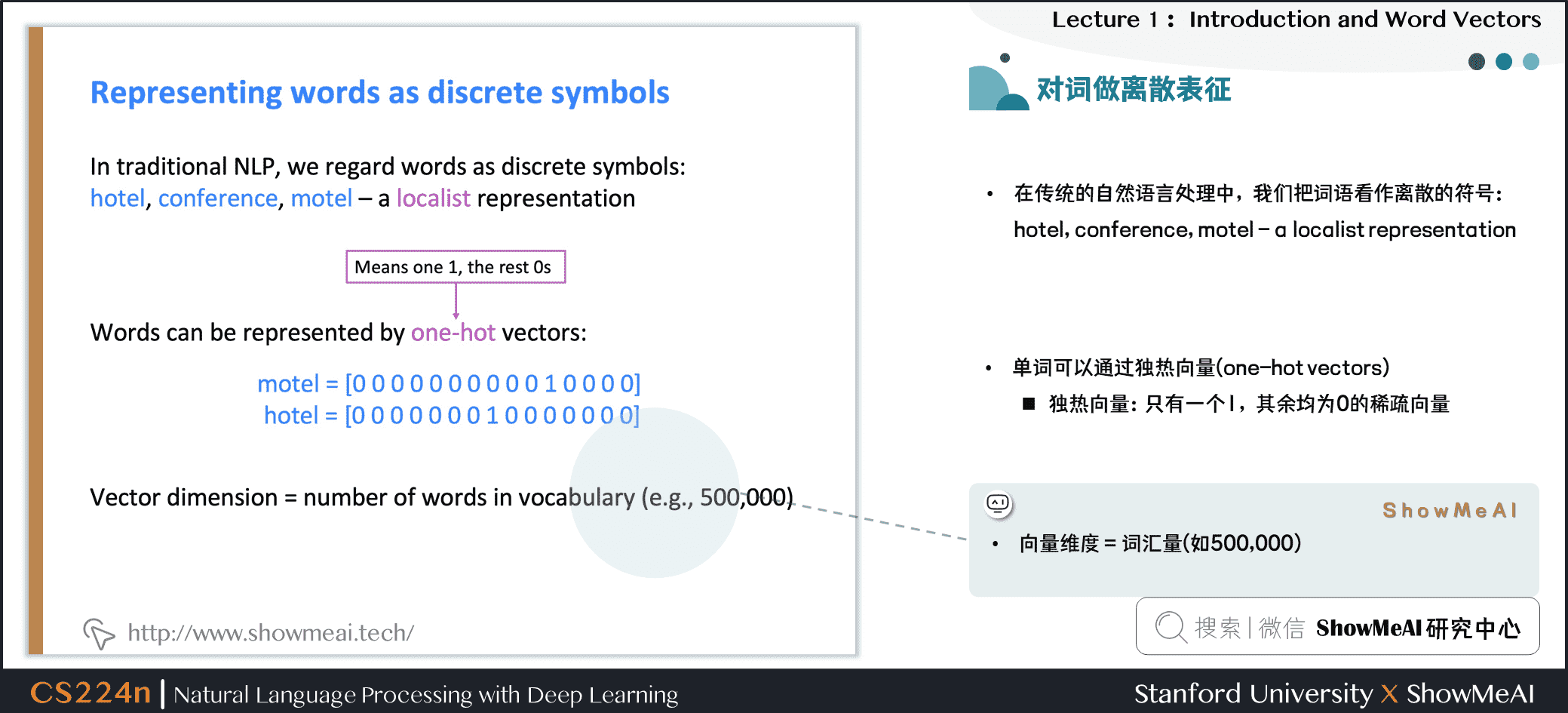
在传统的自然语言处理中，我们会对文本做离散表征，把词语看作离散的符号：例如hotel、conference、motel等。

一种文本的离散表示形式是把单词表征为独热向量(one-hot vectors)的形式

• 独热向量：只有一个1，其余均为0的稀疏向量

在独热向量表示中，向量维度=词汇量(如500,000)，以下为一些独热向量编码过后的单词向量示例：

\[motel = [0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0]
\]

\[hotel = [0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0]
\]

1.6 离散表征的问题

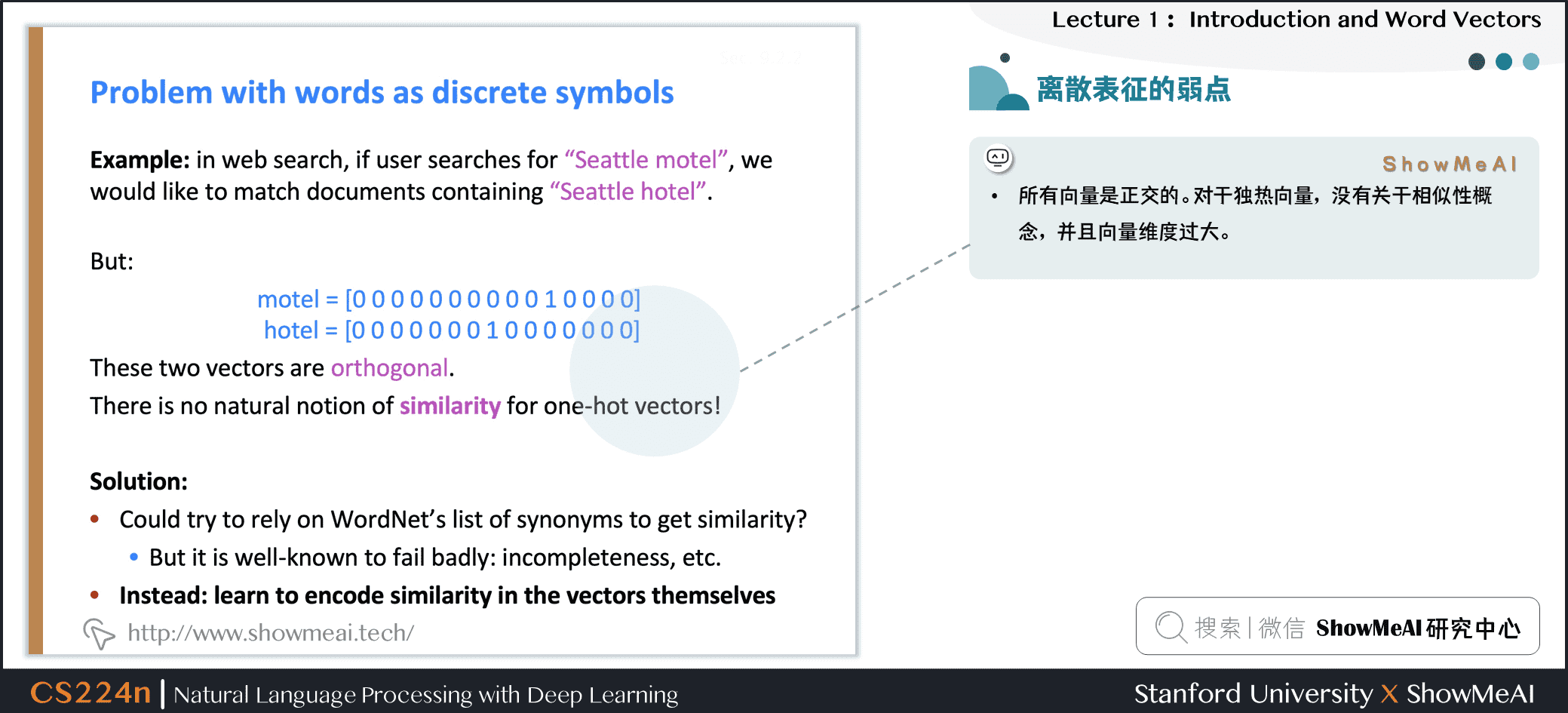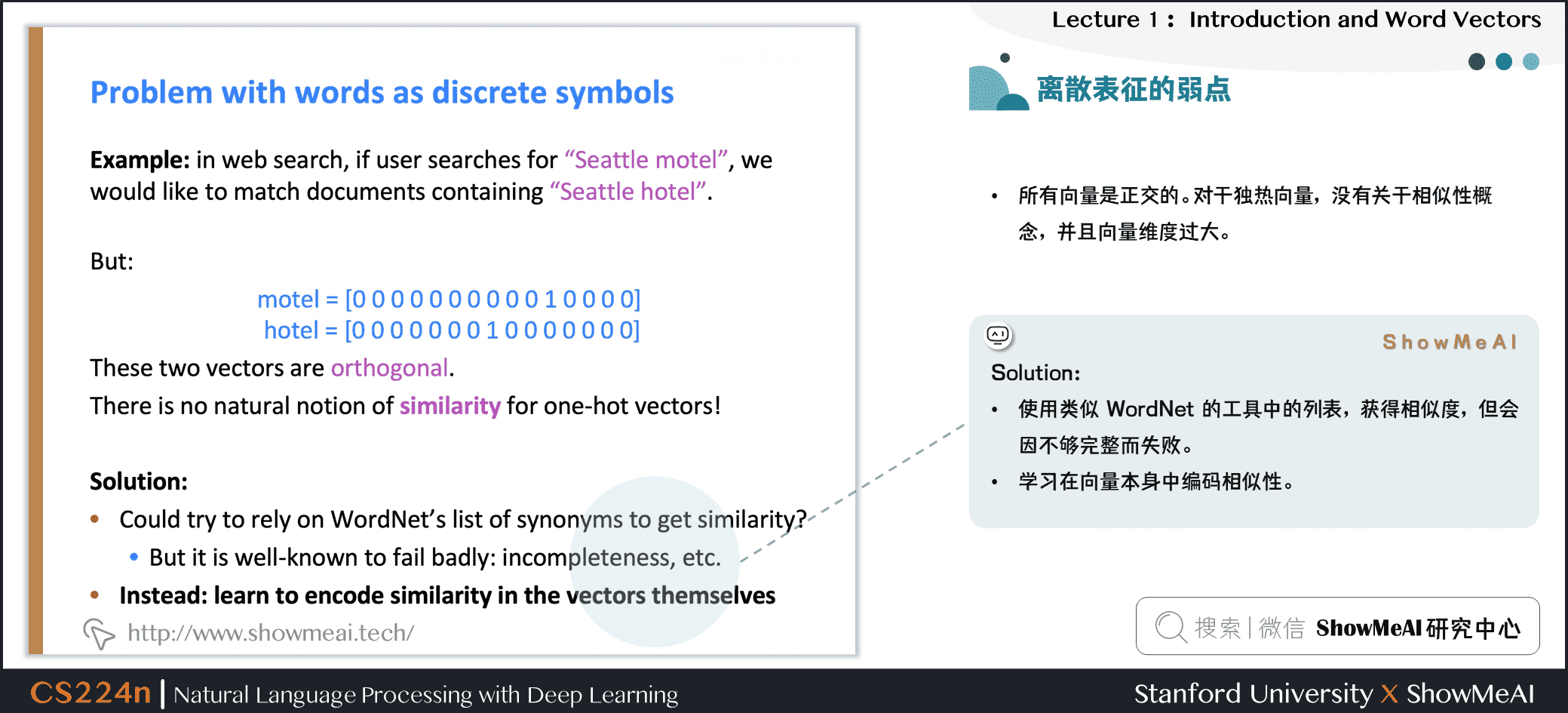
在上述的独热向量离散表征里，所有词向量是正交的，这是一个很大的问题。对于独热向量，没有关于相似性概念，并且向量维度过大。

对于上述问题有一些解决思路：

• ① 使用类似WordNet的工具中的列表，获得相似度，但会因不够完整而失败
• ② 通过大量数据学习词向量本身相似性，获得更精确的稠密词向量编码

1.7 基于上下文的词汇表征

近年来在深度学习中比较有效的方式是基于上下文的词汇表征。它的核心想法是：一个单词的意思是由经常出现在它附近的单词给出的 “You shall know a word by the company it keeps” (J. R. Firth 1957: 11)。

这是现代统计NLP最成功的理念之一，总体思路有点物以类聚，人以群分的感觉。

• 当一个单词 \(w\)出现在文本中时，它的上下文是出现在其附近的一组单词(在一个固定大小的窗口中)
• 基于海量数据，使用 \(w\)的许多上下文来构建 \(w\)的表示

如图所示，banking的含义可以根据上下文的内容表征。

2.Word2vec介绍

2.1 词向量表示

下面我们要介绍词向量的构建方法与思想，我们希望为每个单词构建一个稠密表示的向量，使其与出现在相似上下文中的单词向量相似。

• 词向量(word vectors)有时被称为词嵌入(word embeddings)或词表示(word representations)。
• 稠密词向量是分布式表示(distributed representation)。

2.2 Word2vec原理介绍

Word2vec (Mikolov et al. 2013)是一个学习词向量表征的框架。

核心思路如下：

• 基于海量文本语料库构建
• 词汇表中的每个单词都由一个向量表示（学习完成后会固定）
• 对应语料库文本中的每个位置 \(t\)，有一个中心词 \(c\)和一些上下文(“外部”)单词 \(o\)
• 使用 \(c\)和 \(o\)的词向量来计算概率 \(P(o|c)\)，即给定中心词推断上下文词汇的概率（反之亦然）
• 不断调整词向量来最大化这个概率

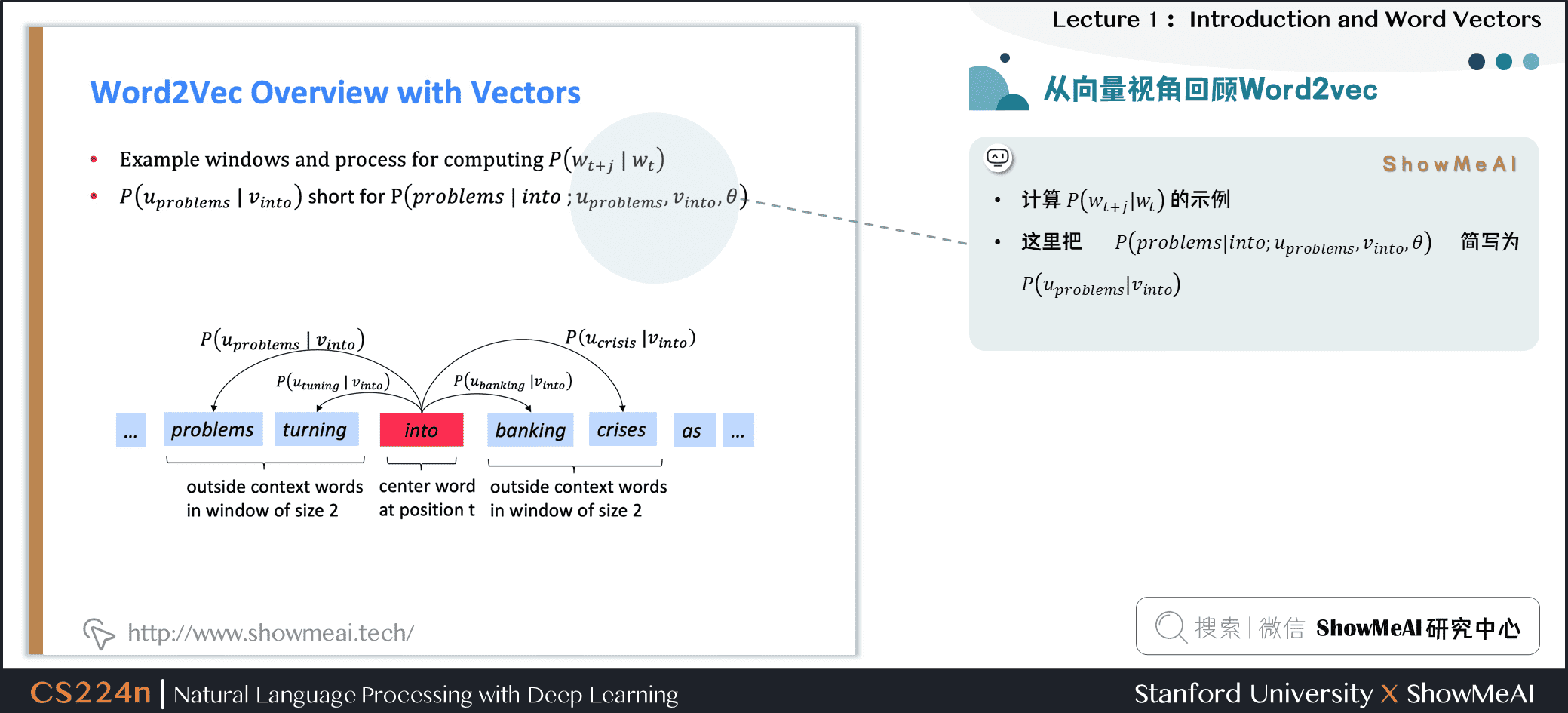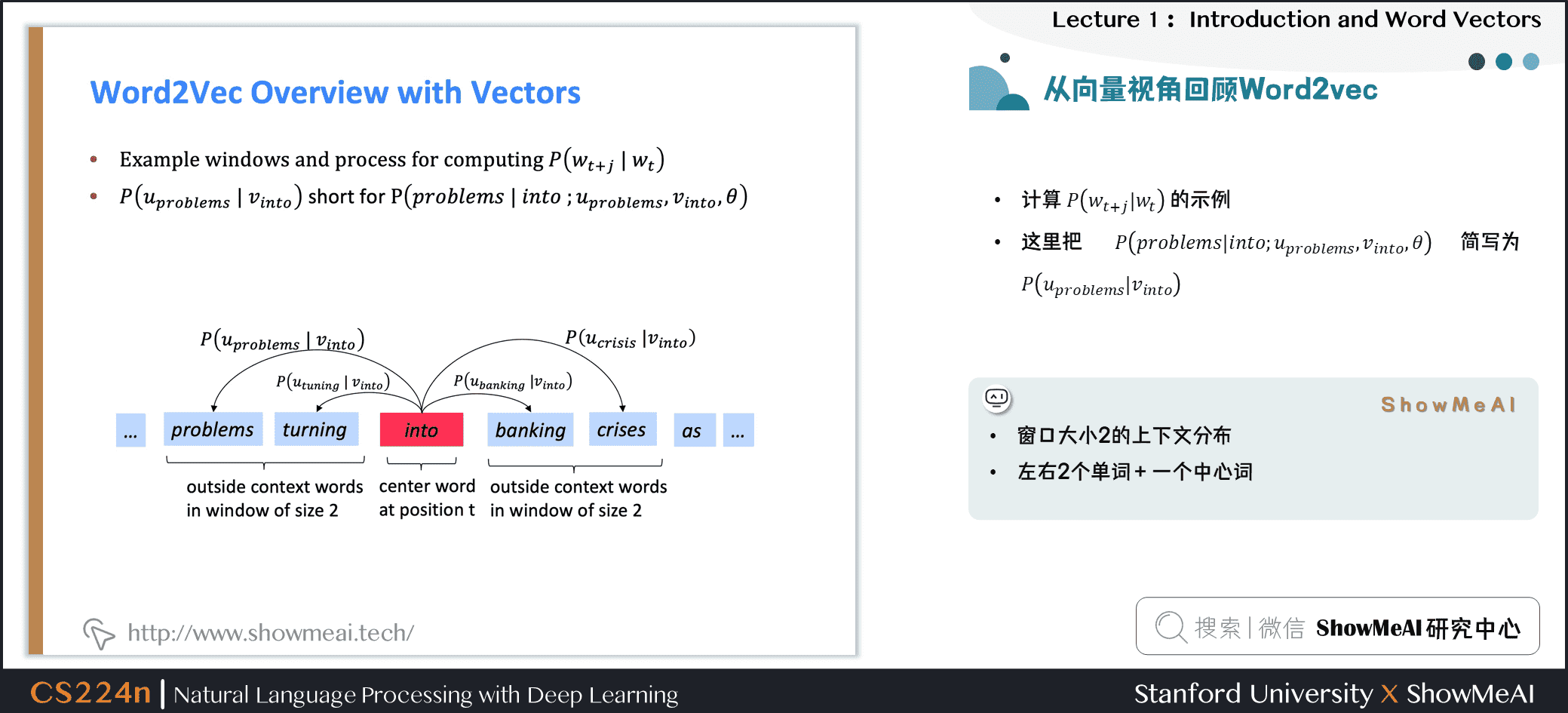
下图为窗口大小 \(j=2\)时的 \(P\left(w_{t+j} | w_{t}\right)\)，它的中心词为 \(into\)

下图为窗口大小 \(j=2\)时的 \(P\left(w_{t+j} | w_{t}\right)\)，它的中心词为 \(banking\)

3.Word2vec 目标函数

3.1 Word2vec目标函数

我们来用数学表示的方式，对word2vec方法做一个定义和讲解。

3.1.1 似然函数

对于每个位置 \(t=1, \cdots, T\)，在大小为 \(m\)的固定窗口内预测上下文单词，给定中心词 \(w_j\)，似然函数可以表示为：

\[Likelihoood = L(\theta) = \prod^{T}_{t=1} \prod_{-m \leq j \leq m \atop j \neq 0} P(w_{t+j} | w_{t} ; \theta)
\]

上述公式中， \(\theta\)为模型包含的所有待优化权重变量

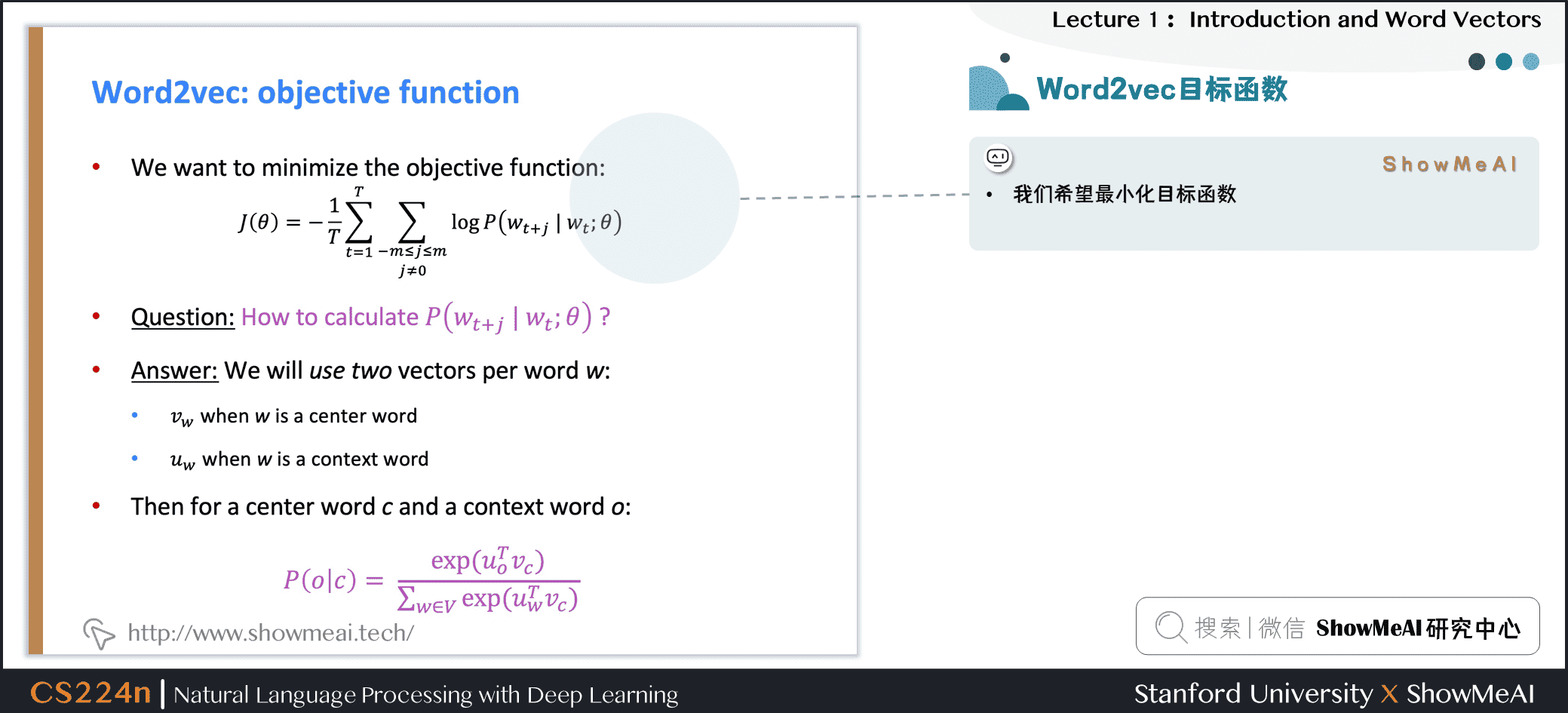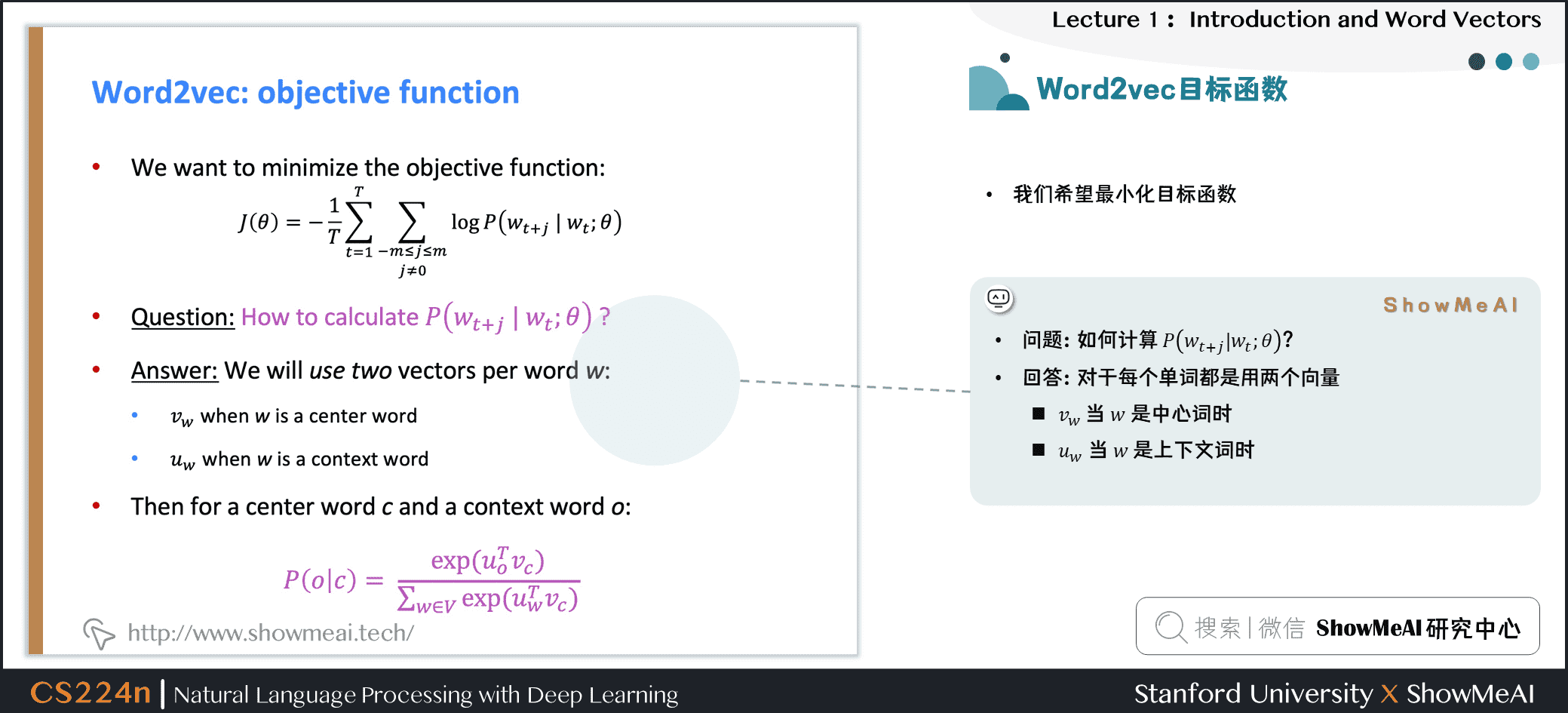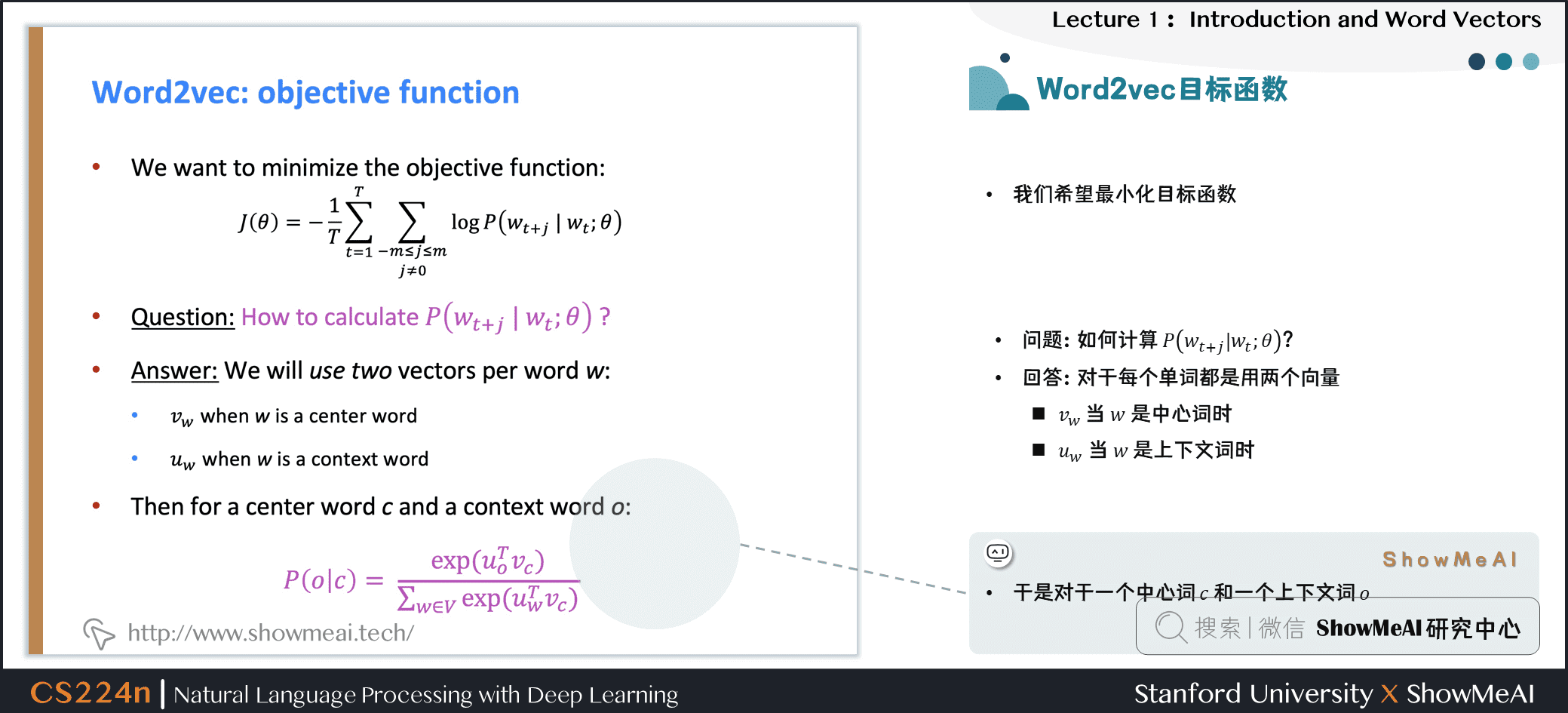
3.1.2 目标函数

对应上述似然函数的目标函数 \(J(\theta)\)可以取作(平均)负对数似然：

\[J(\theta)=-\frac{1}{T} \log L(\theta)=-\frac{1}{T} \sum_{t=1}^{T} \sum_{-m \leq j \leq m \atop j \neq 0} \log P\left(w_{t+j} | w_{t} ; \theta\right)
\]

注意：

• 目标函数 \(J(\theta)\)有时也被称为“代价函数”或“损失函数”
• 最小化目标函数 \(\Leftrightarrow\)最大化似然函数（预测概率/精度），两者等价

补充解读：

• 上述目标函数中的log形式是方便将连乘转化为求和，负号是希望将极大化似然率转化为极小化损失函数的等价问题
• 在连乘之前使用log转化为求和非常有效，特别是做优化时

\[\log \prod_i x_i = \sum_i \log x_i
\]

得到目标函数后，我们希望最小化目标函数，那我们如何计算 \(P(w_{t+j} | w_{t} ; \theta)\)？

对于每个词 \(w\)都会用两个向量：

• 当 \(w\)是中心词时，我们标记词向量为 \(v_w\)
• 当 \(w\)是上下文词时，我们标记词向量为 \(u_w\)

则对于一个中心词 \(c\)和一个上下文词 \(o\)，我们有如下概率计算方式：

\[P(o | c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)}
\]

对于上述公式，ShowMeAI做一点补充解读：

• 公式中，向量 \(u_o\)和向量 \(v_c\)进行点乘
• 向量之间越相似，点乘结果越大，从而归一化后得到的概率值也越大
• 模型的训练正是为了使得具有相似上下文的单词，具有相似的向量
• 点积是计算相似性的一种简单方法，在注意力机制中常使用点积计算Score，参见ShowMeAI文章[C5W3] 16.Seq2Seq序列模型和注意力机制

3.2 从向量视角回顾Word2vec

下图为计算 \(P(w_{t+j} |w_{t})\)的示例，这里把 \(P(problems|into; u_{problems},v_{into},\theta)\)简写为 \(P(u_{problems} | v_{into})\)，例子中的上下文窗口大小2，即“左右2个单词+一个中心词”。

4.Word2vec prediction function

4.1 Word2vec预测函数

回到上面的概率计算，我们来观察一下

\[P(o | c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)}
\]

• 取幂使任何数都为正
• 点积比较 \(o\)和 \(c\)的相似性 \(u^{T} v=u . v=\sum_{i=1}^{n} u_{i} v_{i}\)，点积越大则概率越大
• 分母：对整个词汇表进行标准化，从而给出概率分布

这里有一个softmax的概率，softmax function \(\mathbb{R}^{n} \in \mathbb{R}^{n}\)示例：

将任意值 \(x_i\)映射到概率分布 \(p_i\)

\[\operatorname{softmax}\left(x_{i}\right)=\frac{\exp \left(x_{i}\right)}{\sum_{j=1}^{n} \exp \left(x_{j}\right)}=p_{i}
\]

其中对于名称中soft和max的解释如下（softmax在深度学习中经常使用到）：

• max：因为放大了最大的概率
• soft：因为仍然为较小的 \(x_i\)赋予了一定概率

4.2 word2vec中的梯度下降训练细节推导

下面是对于word2vec的参数更新迭代，应用梯度下降法的一些推导细节，ShowMeAI写在这里做一点补充。

首先我们随机初始化 \(u_{w}\in\mathbb{R}^d\)和 \(v_{w}\in\mathbb{R}^d\)，而后使用梯度下降法进行更新

\[\begin{aligned}
\frac{\partial}{\partial v_c}\log P(o|c) &=\frac{\partial}{\partial v_c}\log \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}\\
&=\frac{\partial}{\partial v_c}\left(\log \exp(u_o^Tv_c)-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\
&=\frac{\partial}{\partial v_c}\left(u_o^Tv_c-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\
&=u_o-\frac{\sum_{w\in V}\exp(u_w^Tv_c)u_w}{\sum_{w\in V}\exp(u_w^Tv_c)}
\end{aligned}
\]

偏导数可以移进求和中，对应上方公式的最后两行的推导

\(\frac{\partial}{\partial x}\sum_iy_i = \sum_i\frac{\partial}{\partial x}y_i\)

我们可以对上述结果重新排列如下，第一项是真正的上下文单词，第二项是预测的上下文单词。使用梯度下降法，模型的预测上下文将逐步接近真正的上下文。

\[\begin{aligned}
\frac{\partial}{\partial v_c}\log P(o|c)
&=u_o-\frac{\sum_{w\in V}\exp(u_w^Tv_c)u_w}{\sum_{w\in V}\exp(u_w^Tv_c)}\\
&=u_o-\sum_{w\in V}\frac{\exp(u_w^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}u_w\\
&=u_o-\sum_{w\in V}P(w|c)u_w
\end{aligned}
\]

再对 \(u_o\)进行偏微分计算，注意这里的 \(u_o\)是 \(u_{w=o}\)的简写，故可知

\[\frac{\partial}{\partial u_o}\sum_{w \in V } u_w^T v_c = \frac{\partial}{\partial u_o} u_o^T v_c = \frac{\partial u_o}{\partial u_o}v_c + \frac{\partial v_c}{\partial u_o}u_o= v_c
\]

\[\begin{aligned}
\frac{\partial}{\partial u_o}\log P(o|c)
&=\frac{\partial}{\partial u_o}\log \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}\\
&=\frac{\partial}{\partial u_o}\left(\log \exp(u_o^Tv_c)-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\
&=\frac{\partial}{\partial u_o}\left(u_o^Tv_c-\log{\sum_{w\in V}\exp(u_w^Tv_c)}\right)\\
&=v_c-\frac{\sum\frac{\partial}{\partial u_o}\exp(u_w^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}\\
&=v_c - \frac{\exp(u_o^Tv_c)v_c}{\sum_{w\in V}\exp(u_w^Tv_c)}\\
&=v_c - \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}v_c\\
&=v_c - P(o|c)v_c\\
&=(1-P(o|c))v_c
\end{aligned}
\]

可以理解，当 \(P(o|c) \to 1\)，即通过中心词 \(c\)我们可以正确预测上下文词 \(o\)，此时我们不需要调整 \(u_o\)，反之，则相应调整 \(u_o\)。

关于此处的微积分知识，可以查阅ShowMeAI的教程图解AI数学基础文章图解AI数学基础 | 微积分与最优化。

• 训练模型的过程，实际上是我们在调整参数最小化损失函数。
• 如下是一个包含2个参数的凸函数，我们绘制了目标函数的等高线。

4.3 训练模型：计算所有向量梯度

\(\theta\)代表所有模型参数，写在一个长的参数向量里。

在我们的场景汇总是 \(d\)维向量空间的 \(V\)个词汇。

5.视频教程

可以点击 B站 查看视频的【双语字幕】版本

6.参考资料

• 本讲带学的在线阅翻页本
• 《斯坦福CS224n深度学习与自然语言处理》课程学习指南
• 《斯坦福CS224n深度学习与自然语言处理》课程大作业解析
• 【双语字幕视频】斯坦福CS224n | 深度学习与自然语言处理(2019·全20讲)
• Stanford官网 | CS224n: Natural Language Processing with Deep Learning

ShowMeAI系列教程推荐

• 大厂技术实现 | 推荐与广告计算解决方案
• 大厂技术实现 | 计算机视觉解决方案
• 大厂技术实现 | 自然语言处理行业解决方案
• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解大数据技术：从入门到精通系列教程
• 图解机器学习算法：从入门到精通系列教程
• 机器学习实战：手把手教你玩转机器学习系列
• 深度学习教程 | 吴恩达专项课程 · 全套笔记解读
• 自然语言处理教程 | 斯坦福CS224n课程 · 课程带学与全套笔记解读

NLP系列教程文章

• NLP教程(1)- 词向量、SVD分解与Word2vec
• NLP教程(2)- GloVe及词向量的训练与评估
• NLP教程(3)- 神经网络与反向传播
• NLP教程(4)- 句法分析与依存解析
• NLP教程(5)- 语言模型、RNN、GRU与LSTM
• NLP教程(6)- 神经机器翻译、seq2seq与注意力机制
• NLP教程(7)- 问答系统
• NLP教程(8)- NLP中的卷积神经网络
• NLP教程(9)- 句法分析与树形递归神经网络

斯坦福 CS224n 课程带学详解

• 斯坦福NLP课程 | 第1讲 - NLP介绍与词向量初步
• 斯坦福NLP课程 | 第2讲 - 词向量进阶
• 斯坦福NLP课程 | 第3讲 - 神经网络知识回顾
• 斯坦福NLP课程 | 第4讲 - 神经网络反向传播与计算图
• 斯坦福NLP课程 | 第5讲 - 句法分析与依存解析
• 斯坦福NLP课程 | 第6讲 - 循环神经网络与语言模型
• 斯坦福NLP课程 | 第7讲 - 梯度消失问题与RNN变种
• 斯坦福NLP课程 | 第8讲 - 机器翻译、seq2seq与注意力机制
• 斯坦福NLP课程 | 第9讲 - cs224n课程大项目实用技巧与经验
• 斯坦福NLP课程 | 第10讲 - NLP中的问答系统
• 斯坦福NLP课程 | 第11讲 - NLP中的卷积神经网络
• 斯坦福NLP课程 | 第12讲 - 子词模型
• 斯坦福NLP课程 | 第13讲 - 基于上下文的表征与NLP预训练模型
• 斯坦福NLP课程 | 第14讲 - Transformers自注意力与生成模型
• 斯坦福NLP课程 | 第15讲 - NLP文本生成任务
• 斯坦福NLP课程 | 第16讲 - 指代消解问题与神经网络方法
• 斯坦福NLP课程 | 第17讲 - 多任务学习(以问答系统为例)
• 斯坦福NLP课程 | 第18讲 - 句法分析与树形递归神经网络
• 斯坦福NLP课程 | 第19讲 - AI安全偏见与公平
• 斯坦福NLP课程 | 第20讲 - NLP与深度学习的未来