强化学习-学习笔记7 | Sarsa算法原理与推导

Sarsa算法是 TD算法的一种，之前没有严谨推导过 TD 算法，这一篇就来从数学的角度推导一下 Sarsa 算法。注意，这部分属于 TD算法的延申。

7. Sarsa算法

7.1 推导 TD target

推导：Derive。

这一部分就是Sarsa 最重要的内核。

折扣回报：$U_t=R_t+\gamma R_{t+1}+\gamma^2 R_{t+2}+\gamma^3 R_{t+3}+\cdots \ \quad={R_t} + \gamma \cdot U_{t+1} $

即将$R_{t+1}$之后都提出一个 $\gamma$ 项，后面括号中的式子意义正为 $U_{t+1}$

通常认为奖励 $R_t$依赖于 t 时刻的状态 $S_t$ 与动作 $A_t$ 以及 t+1 时刻的状态 $S_{t+1}$。

当时对于为什么依赖于 $S_{t+1}$ 有疑问，我回去翻看了学习笔记1：https://www.cnblogs.com/Roboduster/p/16442003.html ，发现并强调了以下这一点：

“值得注意的是，这个 r1 是什么时候给的？是在状态 state s2 的时候给的。”

状态价值函数 $Q_\pi({s_t},{a_t}) = \mathbb{E}[U_t|{s_t},{a_t}]$ 是回报 $U_t$ 的期望；

用折扣回报的变换式，把$U_t$替换掉：$Q_\pi({s_t},{a_t}) = \mathbb{E}[{R_t} + \gamma \cdot U_{t+1} |{s_t}{a_t}]$
有两项期望，分解开：$= \mathbb{E}[{R_t} |{s_t},{a_t}] + \gamma \cdot\mathbb{E}[ U_{t+1} |{s_t},{a_t}]$

下面研究上式的第二项：$\mathbb{E}[ U_{t+1} |{s_t},{a_t}]$

其等于 $\mathbb{E}[ Q_\pi({s_{t+1}},{a_{t+1}}) |{s_t},{a_t}]$

Q 是 U 的期望：所以 $E(E[])=E()$，期望的期望还是原来的期望；这里是逆用这个性质。这么做是为了让等式两边都有 $Q_\pi$ 函数，如下：

于是便得到： $Q_\pi({s_t},{a_t}) =\mathbb{E}[{R_t} |{s_t},{a_t}] + \gamma\cdot\mathbb{E}[ Q_\pi({s_{t+1}},{a_{t+1}}) {s_t},{a_t}] \\ Q_\pi({s_t},{a_t})=\mathbb{E}[{R_t} + \gamma \cdot Q_\pi({S_{t+1}},{A_{t+1}})]$

右侧有一个期望，但直接求期望很困难，所以通常是对期望求蒙特卡洛近似。

$R_t$ 近似为观测到奖励$r_t$

$Q_\pi({S_{t+1}},{A_{t+1}})$用观测到的 $Q_\pi({s_{t+1}},{a_{t+1}})$ 来近似

得到蒙特卡洛近似值$\approx {r_t} + \gamma \cdot Q_\pi({s_{t+1}},{a_{t+1}})$

将这个值表示为 TD target $y_t$

TD learning 目标：让 $Q_\pi({s_t},{a_t}) $ 来接近部分真实的奖励 $y_t$。

$Q_\pi$ 完全是估计，而 $y_t$ 包含了一部分真实奖励，所以 $y_t$ 更可靠。

7.2 Sarsa算法过程

这是一种TD 算法。

a. 表格形式

如果我们想要学习动作价值 $Q_\pi({s_t},{a_t}) $，假设状态和动作都是有限的，可以画一个表来表示：

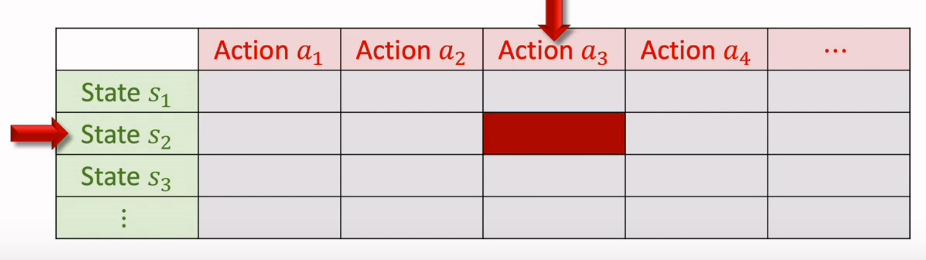
表每个元素代表一个动作价值；

用 Sarsa 算法更新表格，每次更新一个元素；

在表格形式中，每次观测到一个四元组$({s_t},{a_t},{r_t},{s_{t+1}})$，称为一个 transition
根据策略函数 $\pi$ 随机采样计算下一个动作，记作${a_{t+1}}\sim\pi(\cdot|{s_{t+1}})$；
计算TD target: $y_t = {r_t} + \gamma \cdot Q_\pi({s_{t+1}},{a_{t+1}})$，

前一部分是观测到的奖励，后面一部分是对未来动作的打分，$Q_\pi({s_{t+1}},{a_{t+1}})$ 可以通过查表得知。

表最开始是通过一定方式初始化的（比如随机），然后通过不断计算来更新表格。

通过查表，还知道$Q_\pi({s_{t}},{a_{t}})$的值，可以计算：
TD error：$\delta_t = Q_\pi({s_{t}},{a_{t}}) -y_t$；
最后用 $\delta_t$ 来更新：$Q_\pi({s_{t}},{a_{t}}) \leftarrow Q_\pi({s_{t}},{a_{t}}) - \alpha \cdot \delta_t$，并写入表格相应的位置

$\alpha $是学习率。通过TD error 更新，可以让 Q 更好的接近 $y_t$。

每一步中，Sarsa 算法用 $(s_t,a_T,r_t,s_{t+1},a_{t+1})$ 来更新 $Q_\pi$，sarsa，这就是算法名字的由来。

b. 神经网络形式

值得留意的是表格形式的假设：假设状态和动作都是有限的，而当状态和动作很多，表格就会很大，很难学习。

用神经网络-价值网络 $q({s},{a};w)$ 来近似$Q_\pi({s},{a})$，Sarsa算法可以训练这个价值网络。
1. actor-critic 那篇用过 Sarsa 算法，想不起来往下看：
2. q 和 Q 都与策略函数 $\pi$ 有关。
3. 网络参数 $\omega$ 初始时随机初始化，后续不断更新。

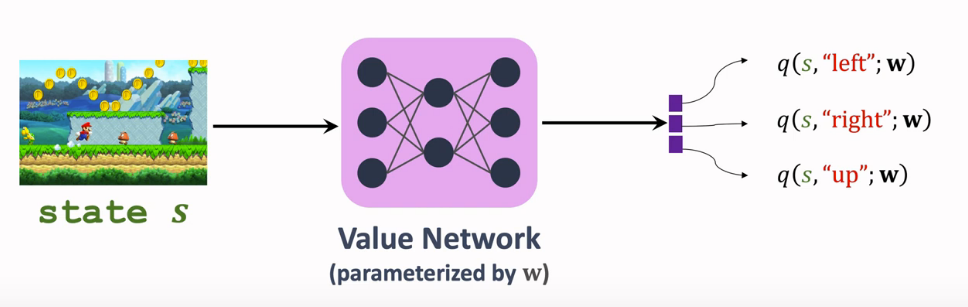
输入状态是 s ，输出就是所有动作的价值

actor-critic 方法中，q 作为 critic 用来评估 actor；用 sarsa 这一 TD 学习算法更新的价值网络。
TD target: $y_t = {r_t} + \gamma \cdot q({s_{t+1}},{a_{t+1}};w)$
TD error：$\delta_t = q({s_{t}},{a_{t}};w) - y_t$
Loss: $\delta_t ^2/2$，我们的目的是通过更新网络参数 w 来降低 Loss；
梯度：$\frac{\partial\delta_t ^2/2}{\partial w} = \delta_t \cdot \frac{\partial q({s_{t}},{a_{t}};w)}{\partial w}$
梯度下降更新 w：$$w \leftarrow w - \alpha \cdot \delta_t \cdot \frac{\partial q({s_{t}},{a_{t}};w)}{\partial w}$$

7.3 一些解惑 / 有什么不同

这一篇跟第二篇价值学习内容看似很接近，甚至在第四篇 actor-critic 中也有提及，可能会困惑这个第七篇有什么特别的，我也困惑了一会儿，然后我发现是自己的学习不够仔细：

第二篇和第四篇的价值网络学习方法并不同。虽然都用到了以TD target 为代表的TD 算法。但是两者的学习函数并不相同！

Sarsa算法学习动作价值函数 $Q_\pi(s,a)$

Actor-Critic 中的价值网络j就是用 Sarsa 训练的

而第二篇 DQN 中的 TD 学习是训练最优动作价值函数:

$Q ^*( s , a ) $

而这种方法在下一篇中很快会提及，这就是 Q-learning 方法。

参考：

TD算法总述

Sarsa算法及其代码