机器学习中 TP FP TN FN的概念

二分类

在二分类问题中，TP FP TN FN 是非常清楚且易于理解的。

TP (True Positive) : 预测为 1 ，真实值也为 1 -> 真阳性

FP (False Positive): 预测为 1 ，真实值为 0 -> 假阳性

TN (True Negative): 预测为 0 ，真实值也为 0 -> 真阴性

FN (False Negative): 预测为 0 ，真实值为 1 -> 假阴性

多分类

多分类问题的 TP FP TN FN 可以通过混淆矩阵来说明。

例如 存在这样一个示例：

y_true = [0, 1, 2, 0, 1, 2]

y_pred = [0, 2, 1, 0, 0, 1]

其混淆矩阵可以如下所示，混淆矩阵中，数字代表的是预测情况的次数，比如第一个方格中的 2 就表示，预测为 0 且真实值也为0的出现的次数为 2 次。

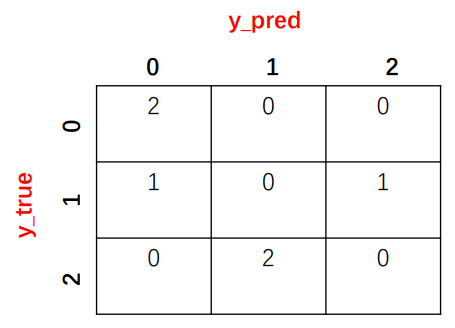
由混淆矩阵，各个类别的 TP FP TN FN 可以如下计算。

• 类别 0:

  TP=2;
  
  TN=0+1+2+0=3;
  
  FP=0+1=1;
  
  FN=0+0=0;

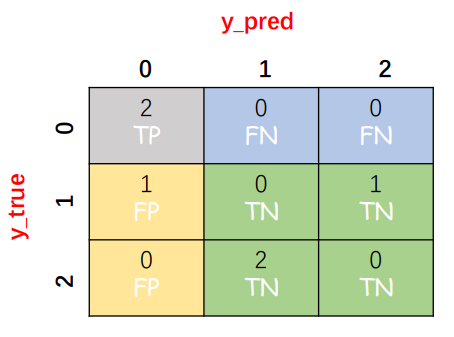
• 类别 1:

  TP=0;
  
  TN=2+0+0+0=2;
  
  FP=0+2=2;
  
  FN=1+1=2;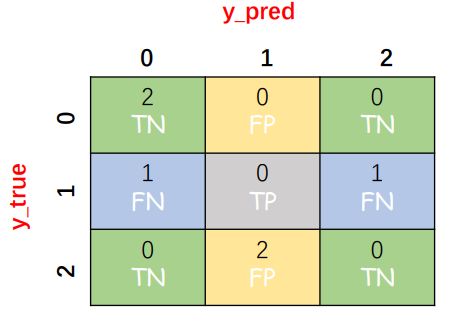

  

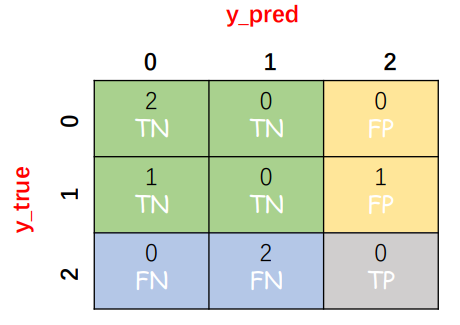
• 类别 2:

  TP=0;
  
  TN=2+0+1+0=3;
  
  FP=0+1=1;
  
  FN=0+2=2;