2021.04.24【NOIP提高B组】模拟 总结

2021.04.24【NOIP提高B组】模拟 总结

T1

题意：有一圈数。两两之间有加法或乘法操作，

问你开始断掉那条边使得剩下的序列经过某种操作后的值最大

看上去是个区间 dp 。然后直接断环成列，找最大值。

光荣 WA

原因：负负得正，最小的两个负数相乘可能比最大的要大

所以多维护一个最小值，乘法的时候多考虑几种情况即可

#include<bits/stdc++.h>
using namespace std;
const int N=105;
int n,m,x[N],f[N][N],g[N][N],mx,ans[N],len; char ch[5],op[N];
int main() {
	scanf("%d",&n),m=n<<1;
	for(int i=1;i<=m;i++) {
		if(i&1)scanf("%s",ch),op[i+1>>1]=ch[0];
		else scanf("%d",&x[i>>1]);
	}
	for(int i=1;i<=n;i++)x[i+n]=x[i],op[i+n]=op[i];
	for(int i=1;i<=m;i++)
		for(int j=1;j<=m;j++)
			f[i][j]=-1<<16,g[i][j]=1<<16;
	for(int i=1;i<=m;i++)f[i][i]=g[i][i]=x[i];
	for(int l=2;l<=n;l++)
		for(int i=1,j=l;j<=m;i++,j++)
			for(int k=i;k<j;k++) {
				if(op[k+1]=='t') {
					f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]);
					g[i][j]=min(g[i][j],g[i][k]+g[k+1][j]);
				} else {
					f[i][j]=max(f[i][j],max(f[i][k]*f[k+1][j],g[i][k]*g[k+1][j]));
					f[i][j]=max(f[i][j],max(f[i][k]*g[k+1][j],g[i][k]*f[k+1][j]));
					g[i][j]=min(g[i][j],min(f[i][k]*f[k+1][j],g[i][k]*g[k+1][j]));
					g[i][j]=min(g[i][j],min(f[i][k]*g[k+1][j],g[i][k]*f[k+1][j]));
				}
			}
	for(int i=1;i<=n;i++) {
		if(f[i][i+n-1]>mx)mx=f[i][i+n-1],ans[len=1]=i;
		else if(f[i][i+n-1]==mx)ans[++len]=i;
	}
	printf("%d\n",mx);
	for(int i=1;i<=len;i++)
		printf("%d ",ans[i]);
}

T2

题意：问你 \(n\) 条变得正凸多边形恰好划分的 \(n-2\) 个三角形中有 \(k\) 个等腰三角形的方案数

不会

\(Update\)

设 \(f_{i,j,k}\) 为从顶点 \(i\) 到顶点 \(j\) 划分出 \(k\) 个等腰三角形个方案数

可得 \(f_{i,j,k}=\sum f_{i,mid,l}*f_{mid,j,k-l-pd(i,j,mid)}\)

其中 \(pd(a,b,c)\) 为判断 \(S_{\triangle abc}\) 是否为等腰三角形

这样时间为 \(O(n^5)\) 会超时

由于是个正多边形，可以压掉 \(i\) 这一维，设 \(f_{i,k}\) 为从 \(1\) 到 \(i\) 有 \(k\) 个等腰三角形的方案数

有 \(f_{i,k}=\sum f_{j,l}*f_{i-j+1,k-l-pd(1,i,j)}\)

复杂度 \(O(n^4)\) 可以通过

\(TLE\) 方法

#include<bits/stdc++.h>
using namespace std;
const int N=55,P=9397;
int n,m,f[N][N][N],pd;
inline int A(int i,int j) {
	return min(abs(i-j),n-abs(i-j));
}
inline void chk(int i,int j,int k) {
	pd=0;
	if(A(i,j)==A(i,k)||A(i,j)==A(j,k)||A(i,k)==A(j,k))pd=1;
}
int main() {
	while(scanf("%d%d",&n,&m)!=EOF) {
		memset(f,0,sizeof(f));
		for(int i=1;i<=n-1;i++)f[i][i+1][0]=1;
		for(int i=1;i<=n-2;i++)f[i][i+2][1]=1;
		for(int len=4;len<=n;len++) {
			for(int i=1,j=len;j<=n;i++,j++) {
				for(int mi=i;mi<=j;mi++) {
					for(int k=0;k<=m;k++) {
						chk(i,j,mi);
						for(int l=0;l<=k-pd;l++)
							(f[i][j][k]+=f[i][mi][l]*f[mi][j][k-l-pd]%P)%=P;
					}
				}
			}
		}
		printf("%d\n",f[1][n][m]);
	}
}

\(AC\) 方法

#include<bits/stdc++.h>
using namespace std;
const int N=55,P=9397;
int n,m,f[N][N],pd;
inline int A(int i,int j) {
	return min(abs(i-j),n-abs(i-j));
}
inline void chk(int i,int j,int k) {
	pd=0;
	if(A(i,j)==A(i,k)||A(i,j)==A(j,k)||A(i,k)==A(j,k))pd=1;
}
int main() {
	while(scanf("%d%d",&n,&m)!=EOF) {
		memset(f,0,sizeof(f));
		f[2][0]=1;
		for(int i=3;i<=n;i++) {
			for(int j=2;j<i;j++) {
				chk(1,i,j);
				for(int k=pd;k<=m;k++)
					for(int l=0;l<=k-pd;l++)
						(f[i][k]+=f[j][l]*f[i-j+1][k-l-pd]%P)%=P;
			}
		}
		printf("%d\n",f[n][m]);
	}
}

T3

题意：有一个 \(n\) 个点的凸多边形，划分成 \(n-2\) 个面积是 \(S_i\) 的三角形，

问 \(\sqrt{\dfrac{\sum_{i=1}^{n-2}(S_i-\overline{S})^2}{n-2}}\) 的最小值，其中 \(\overline{S}\) 是三角形面积平均值

其实就是求 \(\sum_{i=1}^{n-2}(S_i-\overline{S})^2\) 的最小值

看看对于一个多边形

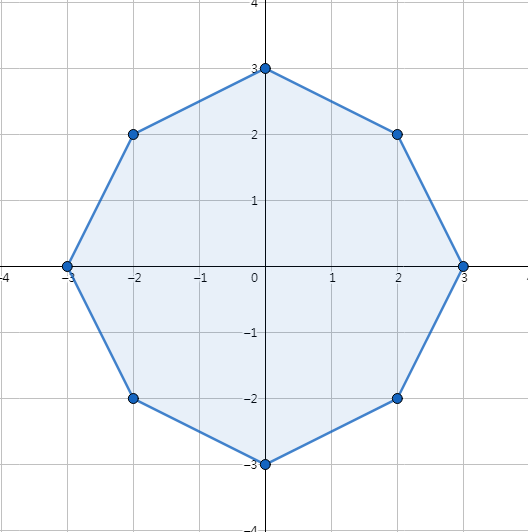
它的最有方案肯定是选择 一条边，并选择一个点

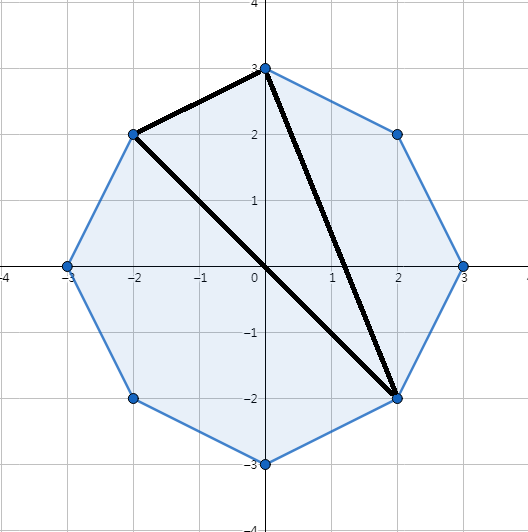
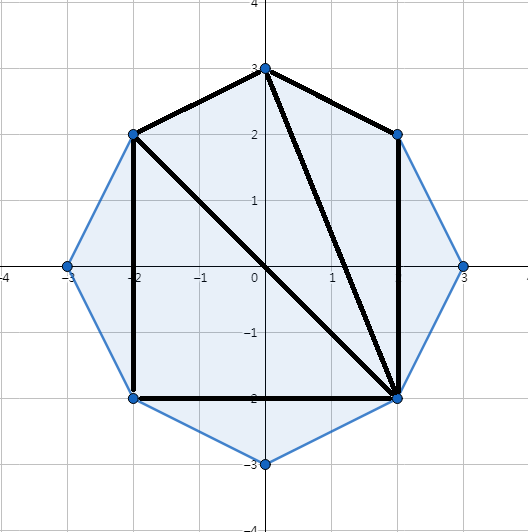
然后将问题分成左右两个子问题

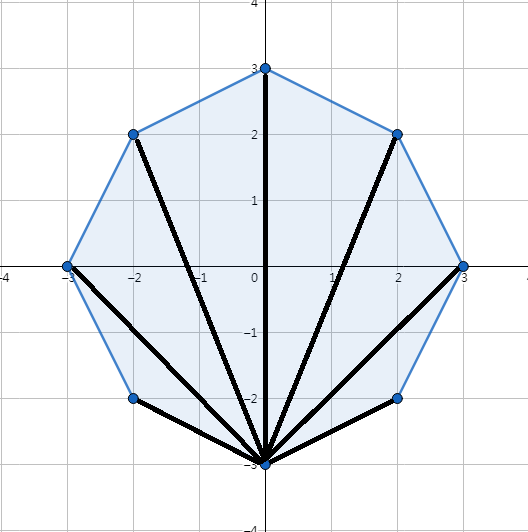
会发现其实左右也是在原有基础选一个点，然后分成更小的子问题

考虑设 \(f_{i,j}\) 为以直线 \(ij\) 为底作三角形的最小值

变成一个区间 dp

如何确定 dp 的顺序：极角排序。

如何求原有的多边形面积（为了平均值）：排完序后， \(\sum_{i=3}^{n} S_{\triangle P_1P_{i-1}P_i}\)

具体点：

写出方程 \(f_{i,j}=\min f_{i,k}+f_{k,j}+(S_{\triangle P_iP_jP_k}-ave)^2\)

然后，切

#include<bits/stdc++.h>
using namespace std;
const int N=55;
typedef double db;
struct poi {
	db x,y;
}p[N];
inline bool cmp(poi u,poi v) {
	register double A=atan2(u.y-p[1].y,u.x-p[1].x),
					B=atan2(v.y-p[1].y,v.x-p[1].x);
	return A==B?u.x<v.x:A<B;
}
inline db sqr(db x) { return x*x; }
inline db dis(int i,int j) {
	return sqrt(sqr(p[i].x-p[j].x)+sqr(p[i].y-p[j].y));
}
inline db area(db a,db b,db c) {
	register db p=(a+b+c)/2.0;
	return sqrt(p*(p-a)*(p-b)*(p-c));
}
inline db sum(int i,int j,int k) {
	return area(dis(i,j),dis(i,k),dis(j,k));
}
db f[N][N],ave;
int n,k;
int main() {
	scanf("%d",&n);
	p[0].x=p[0].y=2100000000;
	for(int i=1;i<=n;i++) {
		scanf("%lf%lf",&p[i].x,&p[i].y);
		if(p[0].y>p[i].y || (p[0].y==p[i].y && p[0].x>p[i].x))
			p[0]=p[i],k=i;
	}
	swap(p[1],p[k]);
	sort(p+2,p+n+1,cmp);
	for(int i=3;i<=n;i++)
		ave+=sum(1,i-1,i);
	ave/=1.0*n-2;
	memset(f,100,sizeof(f));
	for(int i=1;i<n-1;i++)f[i][i+2]=sqr(sum(i,i+1,i+2)-ave);
	for(int i=1;i<=n;i++)f[i][i+1]=f[i][i]=0;
	for(int l=1;l<=n;l++)
		for(int i=1,j=l;j<=n;i++,j++)
			for(int k=i;k<j;k++)
				f[i][j]=min(f[i][j],f[i][k]+f[k][j]+sqr(sum(i,j,k)-ave));
	printf("%.2lf",sqrt(f[1][n]/(1.0*n-2)));
}

T4

有 \(n\) 个位置在 \(x_i\) 的点，总共能选 \(m\) 个点，选的两个点距离不能小于等于 \(d\)

每选一个点能获得 \([l_i,r_i]\) 的范围，问能获得的最大范围

设 \(f_{i,j}\) 表示第 \(i\) 个选了 \(j\) 的最大值

有 \(f_{1,i}=r_i-l_i\) 和 \(\forall 1<i\le n,f_{i,j}=\max f_{i-1,k}+r_j-\max(l_j,r_k)\)

你会发现，这份 20 分的代码，如果打得好，会得到 40 分，甚至——100分

注意：\(x_{i-1}<x_i,l_{i-1}<l_i\)

考虑对 \(\max\) 分类讨论，开两棵权值线段树，要离散化

第一棵，\(r_s\) 里存着 \(f_{i-1,s}-r_s\) 的最大值

第二棵，\(r_s\) 里存着 \(f_{i-1,s}\) 的最大值

因为 \(x\) 递增，所以对于同一个 \(i\) 下的 \(j\) ，若 \(x_{j-1}-x_k>d\)，则 \(x_j-x_k>d\)

可以运用双指针技巧

一开始，现将一些满足 \(x_j-x_k>d\) 的 \(k\) 放进树中

查询第一棵树中 \([l_j+1,2n]\) 的最大值（因为离散化，所以要乘 2）

和第二棵树中 \([1,l_j]\) 的最大值

然后计算 \(f_{i,j}\) 即可

#include<bits/stdc++.h>
using namespace std;
const int N=1005;
struct seg {
	#define ls rt<<1
	#define rs rt<<1|1
	int mx[N<<4];
	void bui(int l,int r,int rt) {
		mx[rt]=-2100000000;
		if(l==r)return;
		register int mid=l+r>>1;
		bui(l,mid,ls);
		bui(mid+1,r,rs);
	}
	void mdy(int p,int v,int l,int r,int rt) {
		if(l==r) { mx[rt]=max(mx[rt],v); return; }
		register int mid=l+r>>1;
		if(p<=mid)mdy(p,v,l,mid,ls);
		else mdy(p,v,mid+1,r,rs);
		mx[rt]=max(mx[ls],mx[rs]);
	}
	int ask(int ql,int qr,int l,int r,int rt) {
		if(ql<=l && r<=qr)return mx[rt];
		if(ql>r || l>qr)return -2100000000;
		register int mid=l+r>>1;
		return max(ask(ql,qr,l,mid,ls),ask(ql,qr,mid+1,r,rs));
	}
	#undef ls
	#undef rs
}LL,RR;

int n,m,D,x[N],L[N],R[N],k,t[N];

int f[N][N],ans;
inline bool cmp(int x,int y) {
	return R[x]<R[y];
}
int main() {
	scanf("%d%d%d",&n,&m,&D);
	for(int i=1;i<=n;i++) {
		scanf("%d%d%d",&x[i],&L[i],&R[i]);
		f[1][i]=R[i]-L[i];
		t[++k]=L[i],t[++k]=R[i];
	}
	sort(t+1,t+k+1);
	k=unique(t+1,t+k+1)-t-1;
	for(int i=1;i<=n;i++) {
		L[i]=lower_bound(t+1,t+k+1,L[i])-t;
		R[i]=lower_bound(t+1,t+k+1,R[i])-t;
	}
	for(int i=2,k,p,q;i<=m;i++) {
		LL.bui(1,n*2,1);
		RR.bui(1,n*2,1);
		k=1;
		for(int j=1;j<=n;j++) {
			for(;x[j]-x[k]>D && k<=n;k++) {
				LL.mdy(R[k],f[i-1][k],1,n*2,1);
				RR.mdy(R[k],f[i-1][k]-t[R[k]],1,n*2,1);
			}
			p=LL.ask(1,L[j],1,n*2,1);
			q=RR.ask(L[j]+1,n*2,1,n*2,1);
			f[i][j]=f[i-1][j];
			if(k>1)f[i][j]=max(f[i][j],max(p-t[L[j]],q)+t[R[j]]);
			ans=max(ans,f[i][j]);
		}
	}
	printf("%d",ans);
}

总结

1. 长知识了
2. 新的区间 dp 模板
3. 极角排序运用
4. 如何暴力+线段树优化