树形DP【初级版】

START:

2021-08-14

10:00:37

在树形DP中，我们可以用数据模拟出一张图，一般是一棵树或是森林，所有的节点一般最多只有一个父节点。并且树里面没有重边或者环，

因此，一颗有N个节点的树有N-1条边。

讲这么多有点抽象，我们借用树形DP最经典的入门题来介绍树形DP的操作：

 

洛谷P1352 没有上司的舞会

题目链接：

 https://www.luogu.com.cn/problem/P1352

 题目详情：

某大学有 n 个职员，编号为 1…n。

他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。

现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数 ri​，但是呢，如果某个职员的直接上司来参加舞会了，

那么这个职员就无论如何也不肯来参加舞会了。

所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

输入格式

输入的第一行是一个整数 n。

第 2 到第 (n+1) 行，每行一个整数，第 (i+1) 行的整数表示 i 号职员的快乐指数 ri​。

第 (n+2) 到第 2n 行，每行输入一对整数 l,k，代表 k 是 l 的直接上司。

输出格式

输出一行一个整数代表最大的快乐指数。

输入输出样例

输入 #1复制

7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5

输出 #1复制

5

说明/提示

数据规模与约定

对于 100% 的数据，保证 1≤n≤6×10^3，−128≤ri​≤127，1≤l,k≤n，且给出的关系一定是一棵树。

建图：节点从1开始，自上层节点是下层节点的直属上司

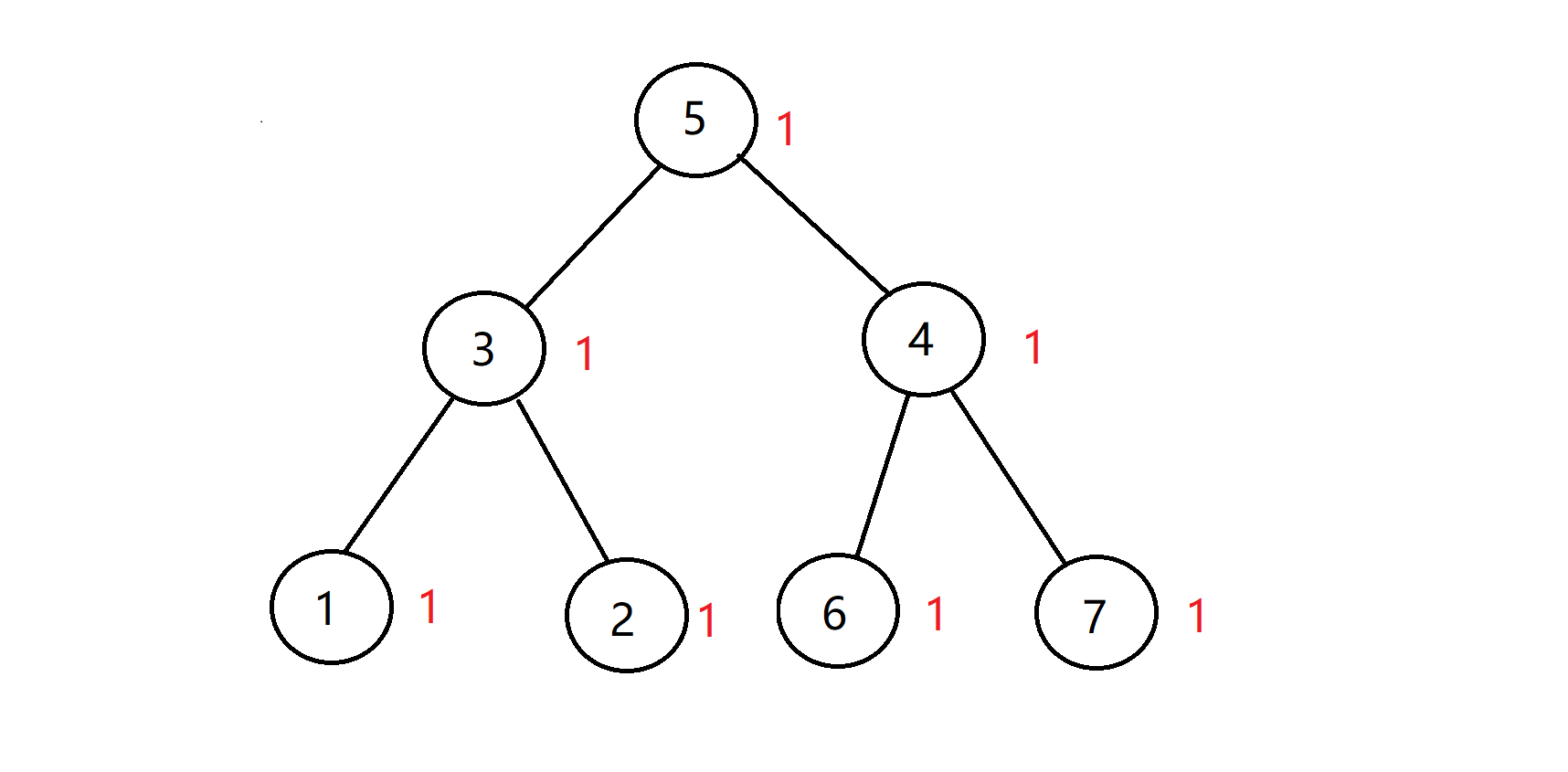
如图所示 ，5是3,4的直属上司，3是1,2的直属上司，4是6,7的直属上司，每个人的快乐指数都是1。

这就是树形DP的最经典的模型。

分析：

我们看5号节点，5号节点有两种选法，一种是选，一种是不选，分别对应两种情况：

1.选：如果选择5号节点，那么他的直系下属3,4就不能选。

2.不选：如果不选择5号节点，那么他的直系下属可以选也可以不选。

我们定义dp[N][2]数组：

dp[N][0]表示在以第N号节点为根的树、在不选择第N号点的情况下的、这棵树的最大快乐指数。

dp[N][1]表示在以第N号及单为根的树、在选择第N号点的情况下的、这棵树的最大快乐指数。

所以我们最后需要求得的答案就是max(dp[5][0],dp[5][1])。

（PS：这里的5是本题所给的样例的最终根节点）

我们在回过头来看任意的根节点 i 与它的子节点的快乐指数的关系：

我们还是先以题目给的样例的5号节点来看，5号节点的子节点有3,4，那么：

对于dp[5][1]，也就是选择5号节点，那么3,4号节点都不能选择，所以dp[5][1]+=dp[3][0]+dp[4][0]

对于dp[5][0]，也就是不选择5号节点，那么3,4号节点可选可不选，

所以取最大值：dp[5][0]+=max(dp[3][0],dp[3][1])+max(dp[4][1],dp[4][0])

所以DP问题最核心的内容——状态转移方程就推出来了，我们用u表示当前的根节点，用v表示根节点u的所有子节点，所以：

 这样每一层的转移方程就确定下来了，但是，现在有一个问题，我们是从最终根节点（样例中是5）开始更新每个节点的最大快乐指数的，但是我们更新上一层需要下一层的快乐指数，也就是说，我们需要先将下一层的点更新，我们怎么实现这一步呢？

其实我认为树形DP的实现过程是回溯的过程，也就是说树形DP实现的过程是从最下面的末端的点开始、自下而上更新完所有的点的，所以我们在写函数的时候需要递归，递归至末端截止，然后开始更新末端的点，然后回溯到上一个点，再更新上一个点，再回溯……直至最终根节点。

好！我们来实现看看吧：

我们先处理输入的数据，我们使用链接表来储存：

在添加边的函数add(int a,int b)中，a是父节点，b是子节点

在预处理函数init()中，我们得先将所有的节点的指向都改为-1，然后再输入下属和上司的编号，再从上司到下属之间连一条线，再用st[N]数组标记子节点b已经有父节点了，表示b节点不是最终根节点，st[b]=true

#include<iostream>
#include<cstring>
using namespace std;
const int N=6005;
int n;
int h[N],ne[N],e[N],idx;
int happy[N];
int dp[N][2];
bool st[N];

void add(int a,int b){
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void init(){
    memset(h,-1,sizeof h);
    for(int i=1;i<=n;i++)scanf("%d",&happy[i]);
    for(int i=0;i<n-1;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        add(b,a);
        st[a]=true;
    }
}

void dfs(int root){

}

int main()
{
    cin>>n;
    init();
    return 0;
}

预处理完毕后，我们来处理核心函数dfs(int u)，

我们先在dfs()中预处理dp[u][1]和dp[u][0]  (dp[u][0]就是0，不需要预处理）

void dfs(int u){
    dp[u][1]=happy[u];

}

然后遍历根节点u的所有子节点，

void dfs(int u){
    dp[u][1]=happy[u];
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];

    }
}

我们在更新dp[u][1]和dp[u][0]的时候需要用到子节点的最大快乐指数，所以我们在更新dp[u][1]和dp[u][0]之前需要再dfs(u的子节点)，来将子节点的最大快乐指数更新。然后再更新当前根节点u的最大快乐指数。

补充完整：

void dfs(int u){
    dp[u][1]=happy[u];
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];
        dfs(j);
        dp[u][1]+=dp[j][0];
        dp[u][0]+=max(dp[j][1],dp[j][0]);
    }
}

我们在main函数里面还要求出最终根节点root，先初始化为1，我们之前用st[N]数组标记过，如果st[i]==false，那么点i就是最终根节点，所以在main函数中，我们应该这样写：

int main()
{
    cin>>n;
    init();
    int root=1;
    while(st[root])root++;
    dfs(root);
    printf("%d\n",max(dp[root][1],dp[root][0]));
    return 0;
}

所以完整代码如下：

#include<iostream>
#include<cstring>
using namespace std;
const int N=6005;
int n;
int h[N],ne[N],e[N],idx;
int happy[N];
int dp[N][2];
bool st[N];

void add(int a,int b){
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void init(){
    memset(h,-1,sizeof h);
    for(int i=1;i<=n;i++)scanf("%d",&happy[i]);
    for(int i=0;i<n-1;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        add(b,a);
        st[a]=true;
    }
}

void dfs(int u){
    dp[u][1]=happy[u];
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];
        dfs(j);
        dp[u][1]+=dp[j][0];
        dp[u][0]+=max(dp[j][1],dp[j][0]);
    }
}

int main()
{
    cin>>n;
    init();
    int root=1;
    while(st[root])root++;
    dfs(root);
    printf("%d\n",max(dp[root][1],dp[root][0]));
    return 0;
}