(AAAI2020 Yao) Graph Few-shot Learning via knowledge transfer

22-5-13 seminar上和大家分享了这篇文章

[0]Graph few-shot learning via knowledge transfer

起因是在MLNLP的公众号上看到了张初旭老师讲的小样本图学习，虽然没看到录像，但是把ppt下下来研究了一下。所以本文中出现的图片许多都是张老师ppt中的图，在张老师的主页上能够找到的这份PPT。

前置知识

图与图表示学习

首先，老生常谈的，自然界中有许多的图数据和应用，包括社交的，安全的，医学的，化学的等等等等。

其中一种方法称为图表示学习，通过一个模型生成嵌入，可以用于下游任务中，包括节点级别的，边级别的，图级别的各种任务。这里的嵌入指的是数据输入模型后得到的输出，往往是数据的低维表示。

这种图表示学习，对于具体的任务，非常依赖充足的标签数据。

于是就遇到了相应的挑战，在图上，有许多数据只有很少的标签数据。例如在社交图中有4000个以上的类别只有不到100个节点，在ins上的毒品交易，天生样本量就很少等等。

于是就发现小样本学习是研究这种问题的一个解决方案。

小样本学习简介

小样本学习的训练流程

概念：小样本学习是一类具有很少监督信息，或者是几个标签的机器学习问题。

小样本学习的目标是，通过补充其他的训练数据来模拟目标的小样本学习任务，来从补充数据中学习到一种元知识。

具体来说，使用的是一种称为n-way k-shot 的学习方式。

如图所示，为一个5-way 1-shot的小样本学习。

way，指的是数据集中类别的数量，图中为5个类别。shot，指的是数据集中每个类别图片的数量，图中每个类别只有一张图片。

小样本学习分为两个阶段，第一个阶段称为元训练，第二个阶段称为元测试。然后每个数据集被分成两组，一组称为支持集，另一组叫查询集。这里需要明确的是，小样本学习会有非常非常多不同的数据集，每个数据集都十分的小，都被分成查询集和支持集两个部分。

在元训练的阶段，首先会用许多不同的数据集对模型进行训练，这些数据集的类别可以毫不相干。如上图所示，meta-training阶段的两个数据集，除了鸟那一类是相同的类别，其他九个类别都不相同。这表明小样本学习并不希望模型学习到类别的特征，而是去学习如何更好的区分类别与类别之间的不同。

在这个阶段中，支持集就可以看做普通机器学习中的训练集，用于模型的训练，而查询集就可以看作是测试集，用于判断模型是否训练到最优

得到训练过的模型以后，进入第二个阶段，称为元测试。首先使用元测试的支持集上训练模型，让模型对该数据集进行一定的微调，让这个模型更好的适应这个元测试阶段的数据集，然后在查询集上运行，查看测试结果。

基于度量的方法

基于度量的方法，代表模型为prototypical net[1]和matching net[2]。

这个方法和我们做嵌入的方法很像，就是通过距离来判断类别。通过计算支持集和查询集的相似度，来学习embedding函数。如图所示，

公式为\(\mathbf{c}_{k}=\frac{1}{\left|S_{k}\right|} \sum_{\left(\mathbf{x}_{i}, y_{i}\right) \in S_{k}} f_{\phi}\left(\mathbf{x}_{i}\right)\)，嵌入函数即为\(f_{\phi}(xi)\),大致是说对于每个类别，取这个类别中所有embedding的平均作为这个类的embedding，称为ck。然后对于一个查询集中的点，输入\(f_{\phi}(xi)\)得到embedding，计算和各个ck之间的距离，来判断是哪个类别。

基于梯度/优化的方法

基于梯度的方法，有时候也被称为基于优化的方法，代表作为MAML[3]。

如下图所示：

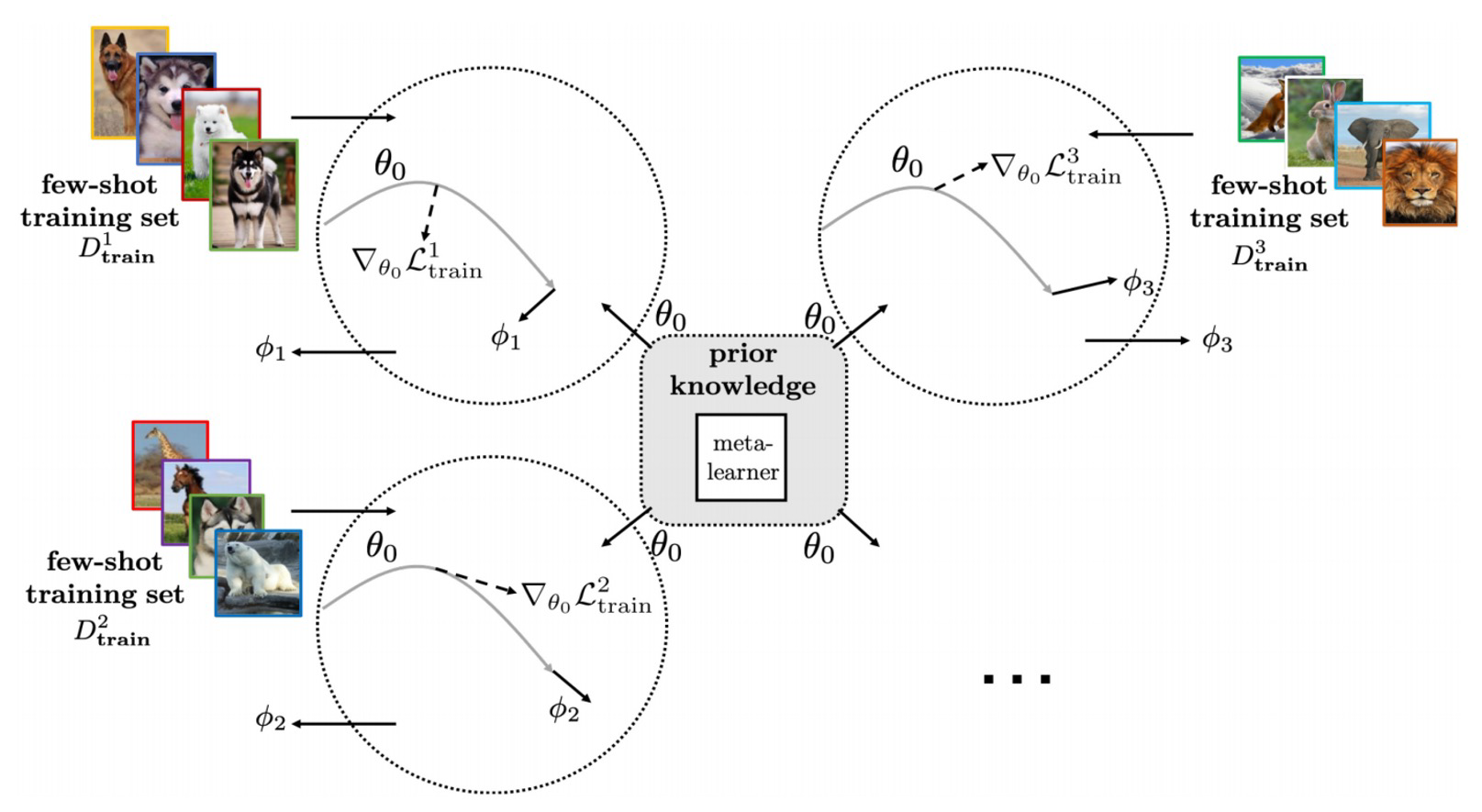
对于这个模型，初始化一个参数θ。在meta training的过程中，对于每个类别，在优化过程中会学习到自己的参数φ。会有各自自己的优化过程。那么通过优化过程平均这个φ，作为meta-testing的初始化。这样一个初始化的参数在学习新的support set时就会学的非常快。

本文内容

本文来自AAAI2020，文章题目叫通过知识迁移的图小样本学习，张初旭老师为本文的第二作者。

和其他图表示学习工作一样，图的小样本学习也分三个类别，即节点级别的，边级别的，图级别的。本文为节点级别的小样本学习。

所有其他领域的方法要迁移到图领域往往会面临一个问题，图特有的数据形式，使得它不只有每个节点自身的特征，还有节点与节点之间的结构关系，如何处理这种结构关系就是将方法应用到图领域的关键。

Method

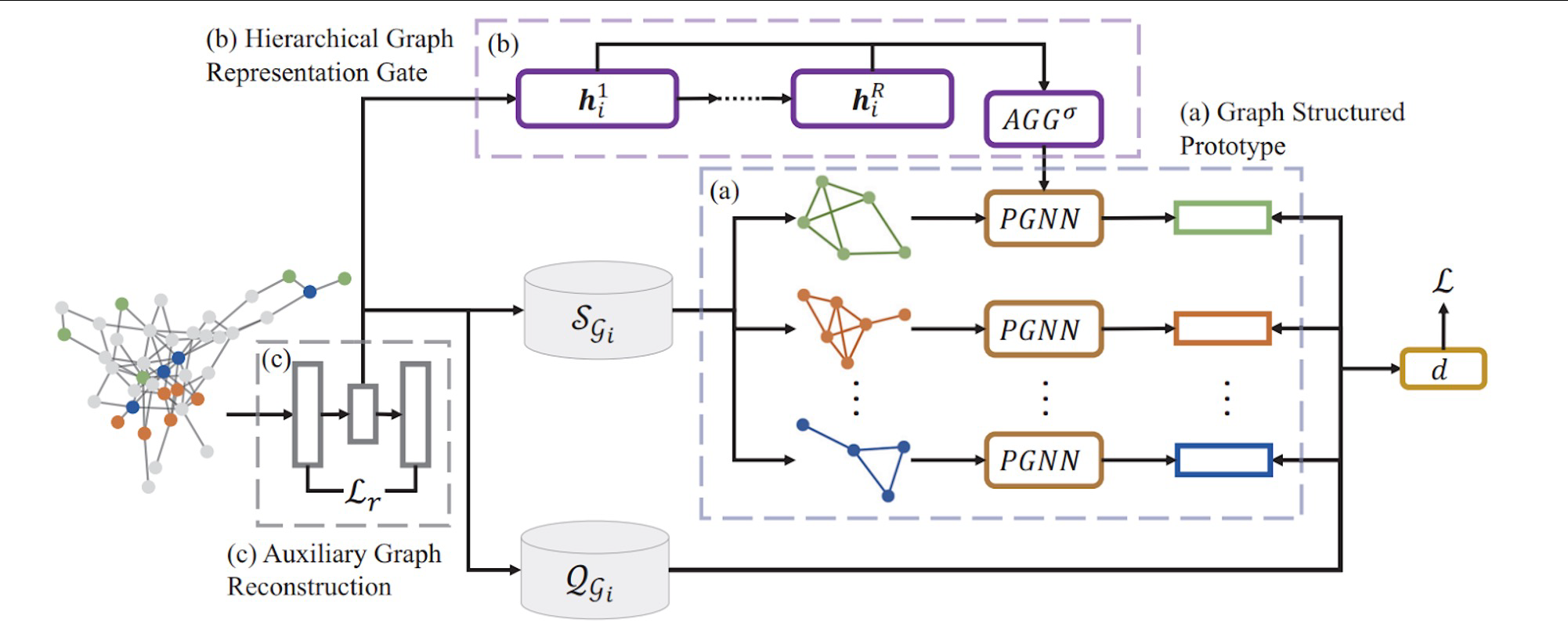
首先，在meta training的阶段，我们拥有几张小样本训练图，可能一张图上有几个类别，每个类别有个位数到十位数左右的节点，例如图上左边的那个子图。

目标是，通过meta training得到的模型，在meta testing阶段，通过少数几个支持集的样本对模型参数进行一定的调整，来预测查询集中的标签。

它的idea是，通过补充图、补充类上训练的模型，进行知识迁移，来提取出一种元知识。所谓的知识迁移，就是指的在元训练阶段和元测试阶段所使用的完全不同的数据集，用别的数据集训练出来的模型做本数据集的任务，就可以叫知识迁移。

这里所谓的补充图，补充类，就是前文小样本学习中提到的补充集。第一张图中有T1，T2，一个T就是一个补充集，放到图上，对于节点分类任务，一个图就是一个数据集，所以称之为补充图。

本文的模型架构具体来说分为三个模块

第零步

对一张图，使用GNN生成各个节点之间的embedding，然后可以直接使用prototypical net的方法，计算个点之间的距离。即每个点的embedding就是一个1*多少多少维的向量，可以根据类别，直接生成每个每个类别的embedding，然后计算查询集之中的embedding和每个类别的embedding之间的距离，也就是这个损失函数。

这就是第0步，啥都不用，直接使用prototypical net，直接生成embedding。

step a

上面的第零步这种情况，就是没有考虑图的结构信息，只使用了每个节点的embedding，为了利用图的结构信息，作者首先增加了a模块，称作图结构原型(graph structure prototype)。

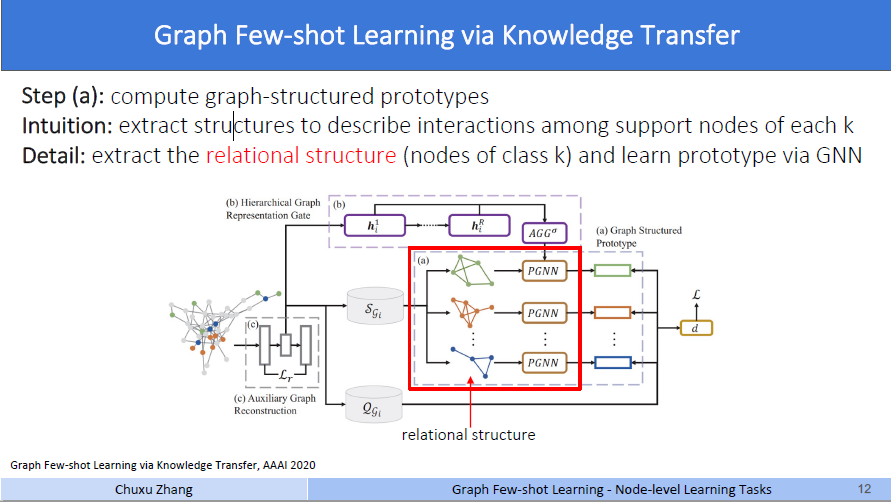
它说，第a步用来计算图结构原型。思想是对每一个类别的支持集节点，提取结构来描述交互作用。

作者在研究如何保留图的结构信息时，做出了一个理论上的假设。详情见论文4.1小节开头，在作者说，在绝大多数情况下，图上的节点有两个重要的角色。一是和类别可能不同的邻居节点的局部交互，二是和距离很远的相同类别的节点的交互，这种交互可以被全局查看，这也就是作者所认为的“全局结构信息”。那么对于第一种作用，就是上面提到的用GNN生成embedding，这个过程就是和邻居节点通过消息传播做聚合的过程，可以体现出和不同类别邻居节点的局部交互。对于第二点，作者说(见图上detail的部分)，提取第k类节点的关系结构，通过GNN学习原型。

具体做法是，通过某些相似性度量方法，将一张图拆分成k个子图，每个子图包括这个类别的全部节点。这里说的相似性度量，文章中提到，是两个节点k跳中相同邻居的数量，或者是节点间的逆拓扑距离。

就以图上这个蓝色的类为例，可以看到这三个节点非常的近，它们k跳的相同邻居肯定很多，那么就认为在子图的结构上，他们是相连的，而这个蓝色的点离这三个点非常的远，所以它只能和这三个点中最近的点有一个连接。(具体细节上这一块是个什么操作我并不很确定，可能需要看代码才能明白)

通过这样子对每个类别构建子图，作者说他捕获了每个类别的关系结构，然后将这每个子图都输入一个PGNN，原型图神经网络，在本文中，就是一个一层的GNN，可以对每个子图的embedding再做一次1跳的消息传播，得到新的embedding，然后做一个池化操作，生成这个类别的embedding ck，式子如下

\[\mathbf{c}_{i}^{k}=\operatorname{Pool}_{j=1}^{n_{i}^{k}}\left(\operatorname{PGNN}_{\phi}\left(\mathcal{R}_{i}^{k}, f_{\theta}\left(\mathcal{S}_{i}^{k}\right)\right)[j]\right)
\]

那么这样得到的embedding可以代表这个类别的信息。然后再拿查询集中的点的embedding和每个类别进行比较，和上文相同。只不过上文第0步这个ck是简单的取平均，而这边是使用PGNN生成的。

step b

然后啊，这个step b模块,称之为分层图表示门控(Hierachical Graph Representation Gate)。这个分层图表示学习，是早期的一个文章[4]，主要是用于图分类。图信息都是层级表示的，例如地图、概念图、流程图等，捕获层级信息将能更加完整高效地表示图。为什么作者要引入这个模块呢？因为在小样本学习中，不止这一张图。一个meta-training 的过程有很多张图，不同的图就会有不同的拓扑结构。对于这个HGR，具体内容如下

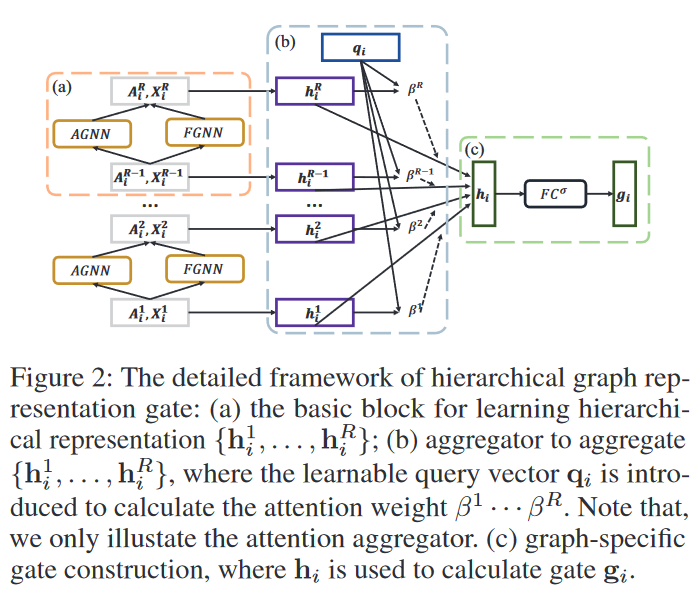
第一步，见橙色的区域a，学习分层图表示的基础模块。对于拿到手的一个邻接矩阵A和特征X，通过这个分层网络的两个步骤，AGNN和FGNN，对图进行分层，可以得到对应每一个层级的表示，或者说embedding。

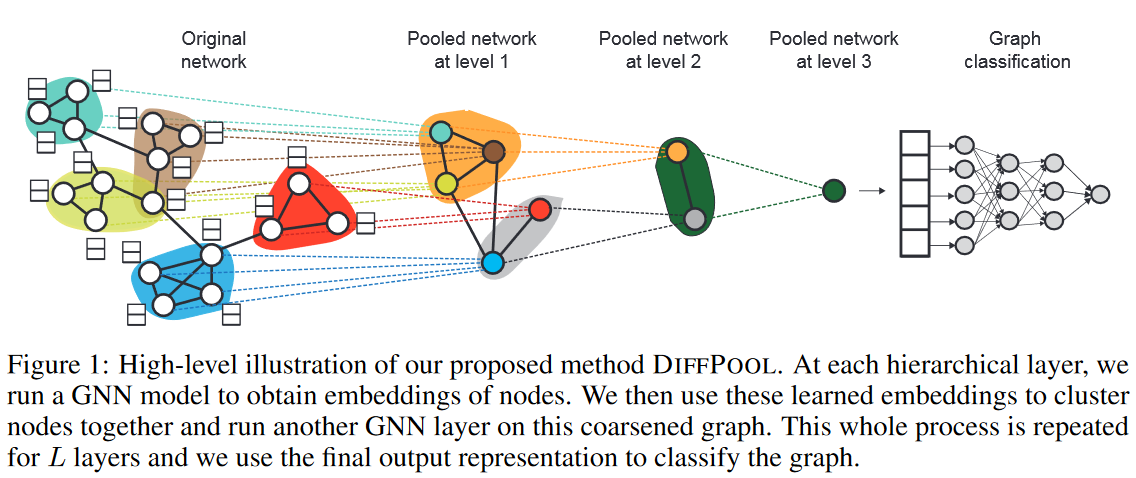
这一块有一个不是很确定的点，具体这个层级的意思。如图，每一个临近节点组成的一个小子图，可以看做一个层级。因为可以看到，图结构中的一个小子图，在第一个层级被聚合成了一个小簇，再到第二层又被聚合成了更小的簇，最后得到了一个嵌入，这个嵌入就可以视为这个图的拓扑信息，在图分类的领域中，这个向量在后续通过神经网络训练来实现图分类。

所以我们理解这个第一步的功能，就是得到图在图分类层面的表示，也就是每一个层级图的嵌入。

第二步，回到这个Fig2，见蓝色的区域b。在得到这个层级的特征表示后，做一个池化操作可以得到这个层级的图表示，对每个层级做这个操作以后，就得到了引入一个qi，可以认为是一种注意力机制，乘上每一个embedding做聚合，得到了这个图的嵌入表示hi。那么这个hi，作者就认为，视作这个图结构的高度概括，是这张图的图表示。

第三步，见绿色的区域c。文中4.2节的最后一段说到，前人的研究表明，相似的图在GNN上会有相似的参数。所以作者引入了一个门控函数来弥补图的具体化信息。一般来说，遇到的所谓的门控，基本上都是矩阵的哈达玛积。先将hi放入一个可学习的线性层，\(\mathbf{g}_{i}=\mathcal{T}\left(\mathbf{h}_{i}\right)=\sigma\left(\mathbf{W}_{g} \mathbf{h}_{i}+\mathbf{b}_{g}\right)\)，然后和上文中step a中的PGNN的参数做一次哈达玛积，也就是矩阵中对应位置的值做乘积。

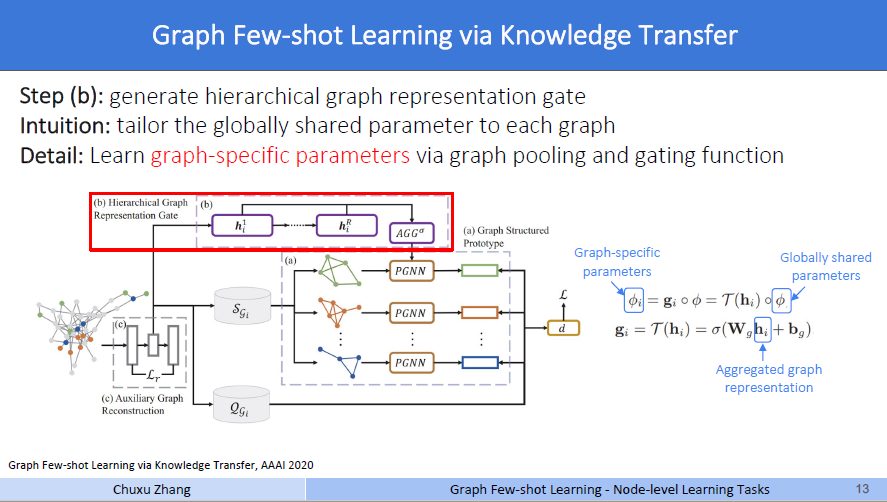
如图右边的公式所示啊，\(\phi\)就是step a中PGNN训练的参数，这里称为全局共享参数，一般来说就是一个权重矩阵。经过\(\phi_{i}=\mathbf{g}_{i} \circ \phi=\mathcal{T}\left(\mathbf{h}_{i}\right) \circ \phi\)后，得到的\(\phi_i\)，称之为图具体参数，就是说这时候我的PGNN的参数，针对不同的数据集的补充图，做过不同的特化。

step c

为什么有这个第三步呢，作者说，仅仅靠这个，非常遥远的这个匹配损失，来训练本身的节点表示，是非常非常困难的。第一步所使用的损失函数

\[\mathcal{L}_{i}^{k}=-\sum_{\left(\mathbf{x}_{i, j}^{q_{i}}, y_{i, j}^{q_{i}}\right) \in \mathcal{Q}_{i}^{k}} \log \frac{\exp \left(-d\left(f_{\theta}\left(\mathbf{A}, \mathbf{x}_{i, j}^{q_{i}}\right), \mathbf{c}_{i}^{k}\right)\right)}{\sum_{k^{\prime}} \exp \left(-d\left(f_{\theta}\left(\mathbf{A}, \mathbf{x}_{i, j}^{q_{i}}\right), \mathbf{c}_{i}^{k^{\prime}}\right)\right)},
\]

同时负责了这个PGNN，这个HGRG，和原本的这个嵌入函数fθ的优化过程。估计是单靠这一个损失函数训练的效果不是很好，那么作者就说，在生成节点的embedding表示这一步，要新增一个新的限制，来控制这个原本的embedding节点的质量，称作补充图重构。

具体来说，用一个图的自编码器来重构这个图。增加了损失函数

\[\mathcal{L}_{r}\left(\mathbf{A}_{i}, \mathbf{X}_{i}\right)=\left\|\mathbf{A}_{i}-\mathrm{GNN}_{d e c}\left(\mathbf{Z}_{i}\right) \mathrm{GNN}_{d e c}^{T}\left(\mathbf{Z}_{i}\right)\right\|_{F}^{2},
\]

Zi就是一个编码器，也就是一个GNN，生成图中每个节点的表示，然后通过一个解码器，在乘以其转置，得到的这个结果用于描述图的结构，和邻接矩阵相减做F范数。

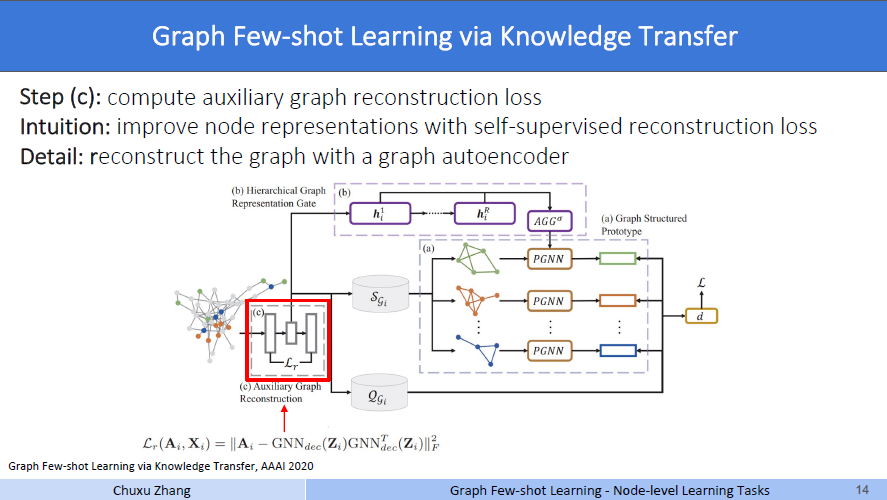
这个损失函数的含义是，要求图的结构尽量的不变，然后得到正常的embedding。Intuition部分说这是一种自监督的方法，用自监督的重构损失来提高节点标识的质量。

这样，损失函数就变成了

\[\min _{\Theta} \sum_{i=1}^{N_{t}} \mathcal{L}_{i}+\gamma \mathcal{L}_{r}\left(\mathbf{A}_{i}, \mathbf{X}_{i}\right)
\]

Algorithm

最后是总体的算法：

初始化参数Θ，
采样一些图，得到领接矩阵和特征矩阵
对于每一个图，采样出支持集和查询集
计算embedding和重构损失Lr stepc中的内容
计算这个图的图表示，和参数φ做门控 stepb中的内容
构建关系图并计算图原型
计算图原型和查询集中embedding的距离，并构成损失函数Li
反向传播更新参数

experiment

setting

在论文第五章节的右边部分，作者说到，他们沿用了传统的小样本学习设置。对于每一张图，每个类别中去N的带标签的节点来作为支持集，身下的节点都是用于评估表现的查询集，如下图。

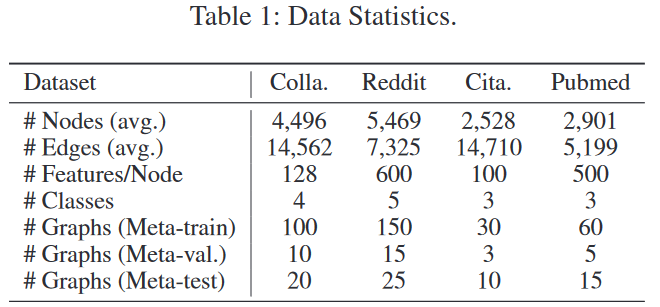
由于step b的分层网络有一个注意力机制qi，所以实验了使用mean和attention两种情况，称为GFL-mean和GFL-att。GFL-mean表示对hi的聚合采用的平均池化(论文中等式6)，GFL-att表示对hi的聚合采用的注意力聚合(论文中等式7)。

result

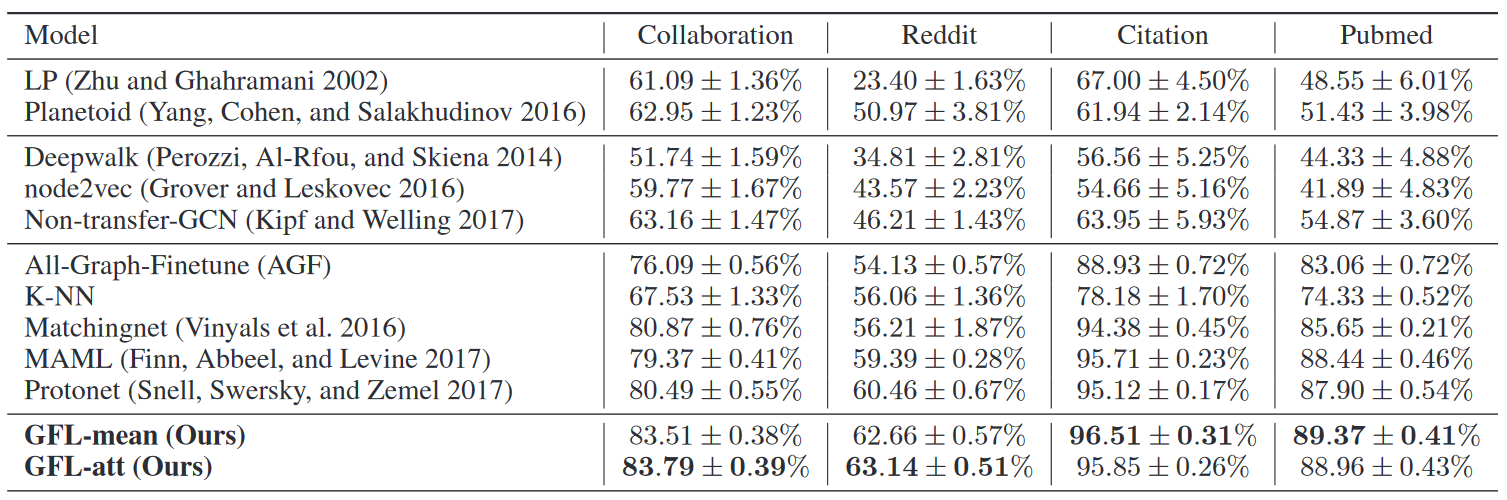
KNN往上都传统的图神经网络方法，可以看到效果都不咋样。在Meta-train阶段只有100多个甚至几十个节点训练出来的模型，在剩下的查询集上表现糟糕是理所应当的。

三种经典的小样本学习表现很好，说明即使没有考虑图的结构信息，全靠节点信息，小样本学习方法依旧可以奏效。

本文的方法在原本的小样本方法上更进一步，大概提升在二到三个点左右，可以看到这么复杂的结构还是有用的。

对我的启发

小样本学习有一种方法称作MAML，和我正在做的某个方法有一定相似之处，目前正在研究如何考虑结构信息，将原方法迁移到图上来。那么MAML乃至整个小样本学习迁移到图领域所做的方法，对我现在这个方法迁移到图上能有一定的参照。

引用文献：

[1] Snell J, Swersky K, Zemel R. Prototypical networks for few-shot learning[J]. Advances in neural information processing systems, 2017, 30.

[2] Vinyals O, Blundell C, Lillicrap T, et al. Matching networks for one shot learning[J]. Advances in neural information processing systems, 2016, 29.

[3] Finn C, Abbeel P, Levine S. Model-agnostic meta-learning for fast adaptation of deep networks[C]//International conference on machine learning. PMLR, 2017: 1126-1135.

[4] Ying Z, You J, Morris C, et al. Hierarchical graph representation learning with differentiable pooling[J]. Advances in neural information processing systems, 2018, 31.