多项式回归 & pipeline & 学习曲线 & 交叉验证

多项式回归就是数据的分布不满足线性关系，而是二次曲线或者更高维度的曲线。此时只能使用多项式回归来拟合曲线。比如如下数据，使用线性函数来拟合就明显不合适了。

接下来要做的就是升维，上面的真实函数是：$ y = 0.5x^2 + 2x + 5\(。而样本数据的形式是(x, y)，以这种方式只能训练出\)y = ax + b\(。所以，手动构造\)x^2\(项，让样本的形式变为：\)(x, x^2, y)\(。这样，增加了一个\)x^2$特征，再使用线性回归就可以得到形如 \(y = ax^2 + bx + c\) 的拟合曲线。

使用线性回归取拟合这个二次曲线,当然，结果一定是欠拟合：

from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(x, y)
y_predict = reg.predict(x)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict, color="b")
plt.show()

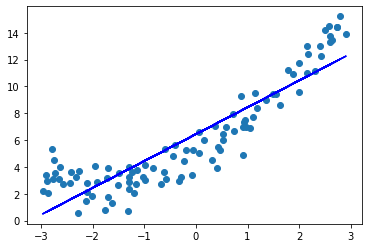
增加\(x^2\)作为新的特征，再拟合，效果还不错：

new_cow = x ** 2
x_new = np.hstack([x, new_cow])     # 将x^2放在最后一列
reg_2 = LinearRegression()
reg_2.fit(x_new, y)
y_predict2 = reg_2.predict(x_new)

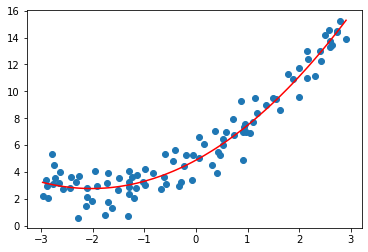
使用sklearn中的多项式回归

from sklearn.preprocessing import PolynomialFeatures
poly_feature = PolynomialFeatures(degree = 2)    # 最高为2阶多项式
poly_feature.fit(X)
X_poly = poly_feature.transform(X)

PolynomialFeatures用于将x的所有可能的幂次都算出来

\(x=(a, b)\), degree=3，transform(X)会返回6个值，分别表示(1, a, b, \(a^2\), ab, \(b^2\))

xx = np.arange(0, 100)
xx = xx.reshape(50, 2)  # 两个特征
print(xx[:3])
poly_feature = PolynomialFeatures(degree = 2)   # 最高次幂为2
poly_feature.fit_transform(xx[:3])

结果是：

[[0 1]
 [2 3]
 [4 5]]
[[ 1.,  0.,  1.,  0.,  0.,  1.],
[ 1.,  2.,  3.,  4.,  6.,  9.],
[ 1.,  4.,  5., 16., 20., 25.]]

使用 PolynomialFeatures和LinearRegression进行多项式回归

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
# 数据集
x = np.random.uniform(-3, 3, size=100)
y = 0.5 * (x ** 2) + 2 * x + 5 + np.random.normal(0, 1, 100)
X = x.reshape(-1, 1)
poly_feature = PolynomialFeatures(degree = 2)    # 最高为2阶多项式
reg_poly = LinearRegression()
# 转换参数，升维
poly_feature.fit(X)
X_poly = poly_feature.transform(X)
# 进行多项式回归
reg_poly.fit(X_poly, y)
y_predict = reg_poly.predict(X_poly)

效果如下：

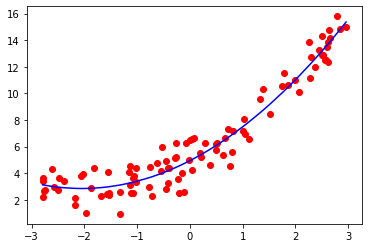
使用Pipeline 封装拟合的细节

poly_pipeline = Pipeline([
    ("poly", PolynomialFeatures(degree=2)),
    ("std_scaler", StandardScaler()),
    ("line_reg", LinearRegression())
])

如此，创建了一个具有特征转换、数据归一化、线性拟合为一体的pipeline。使用方式和 LinearRegression一样。只是此时已经不需要收到的将x转换为多项式形式，也不需要手动的进行数据归一化。

poly_pipeline.fit(X, y)
y_predict = poly_pipeline.predict(X)

过拟合 & 欠拟合

对pipeline进行简单的封装，以下方法只需要传入一个参数就可以得到一个可用的多项式回归对象。

# 使用多项式回归，只需要传入一个参数degree
def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree)),
        ("std_scaler", StandardScaler()),
        ("line_reg", LinearRegression())
    ])

还是之前的数据，进行2阶多项式拟合，使用均方误差评估算法：

poly_reg = PolynomialRegression(2)
poly_reg.fit(X, y)
y_predict = poly_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)])
# 均方误差： 1.117776648943851

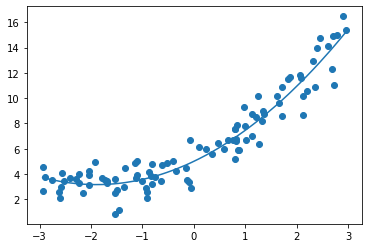
尝试更高维的数据：

10阶：

均方误差： 1.082746862641965

100阶：

均方误差： 0.4988841593798084

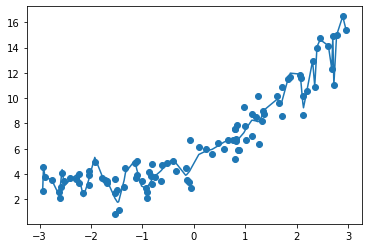
使用如下方式绘制100阶曲线更准确(使x等距，而不是随机)：

xx = np.linspace(-3, 3, 100)
xx = xx.reshape(-1,1)
yy = poly_reg100.predict(xx)
plt.scatter(xx, yy)
plt.axis([-3, 3, 0, 10])
plt.plot(np.sort(xx), y_predict100[np.argsort(x)], color="r")

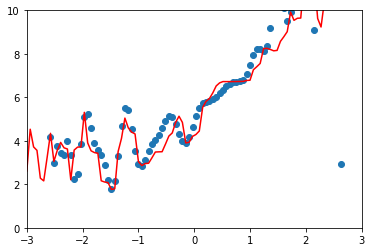
均方误差越来越小，拟合程度越来越高，但是毫无意义。算法对过多的噪音数据进行了过拟合。实际上模型的泛化效果很差。

学习曲线

如果训练数据有m个，那么循环m次，每次都计算对于训练数据和测试数据的MSE，观察变化的趋势。

def plot_learning_curve(reg, X_train, X_test, y_train, y_test):
    # 使用线性回归绘制学习曲线
    train_score = []
    test_score = []
    for i in range(1, len(X_train)):
        reg.fit(X_train[:i], y_train[:i])
        y_train_predict = reg.predict(X_train[:i])
        y_test_predict = reg.predict(X_test)
        train_score.append(mean_squared_error(y_train_predict, y_train[:i]))
        test_score.append(mean_squared_error(y_test_predict, y_test))
    plt.axis([0,75,0, 10])
    plt.plot([i for i in range(1, len(X_train))], np.sqrt(train_score), label="train")
    plt.plot([i for i in range(1, len(X_train))], np.sqrt(test_score), label="test")
    plt.legend()
    plt.show()

线性回归的学习曲线

reg_line = LinearRegression()
plot_learning_curve(reg_line, X_train, X_test, y_train, y_test)

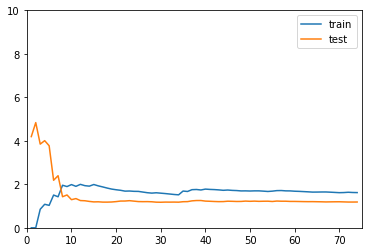
二阶线性回归的学习曲线

reg_2 = PolynomialRegression(2)    # 使用pipeline
plot_learning_curve(reg_2, X_train, X_test, y_train, y_test)

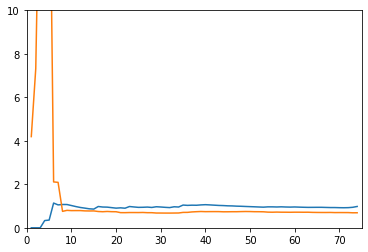
20阶线性回归的学习曲线

reg_2 = PolynomialRegression(20)    # 使用pipeline
plot_learning_curve(reg_2, X_train, X_test, y_train, y_test)

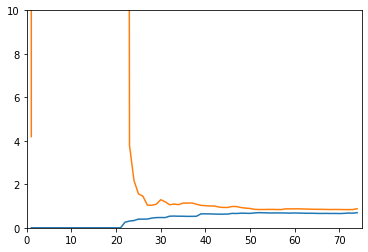
分析

没有对比就没有伤害。前两个都收敛，但是二阶的MSE更低，所以线性回归得到的使欠拟合的曲线。20阶的训练数据表现很好，但是测试数据表现不行，所以使过拟合（其实也还要，用更高阶的函数可能会更明显）

手动寻找最优参数

就是遍历所有参数，找score最高的参数。

from sklearn.neighbors import KNeighborsClassifier
best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)
        if score > best_score:
            best_k, best_p, best_score = k, p, score
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)

交叉验证

k-折交叉验证（k-fold cross validation），之前随机选取的叫简单交叉验证（hold -out cross validation）。k折，就是将训练集分为k份，每次只用k-1组数据训练，用剩下的一组计算score。

原来的测试集就完全不使用，等到模型训练完毕后，再使用测试集计算模型的性能。简单交叉验证用测试集计算score，测试集中的数据也影响了参数的选择。有可能会导致模型对训练数据和测试数据的过拟合。

使用 k-折交叉验证得到的score是一个数组，因为需要进行k次拟合。

from sklearn.model_selection import cross_val_score
knn_clf = KNeighborsClassifier()
cross_val_score(knn_clf, X_train, y_train, cv=3)
# array([0.98895028, 0.97777778, 0.96629213])

网格搜索（待定）

实际上也是使用CV寻找最优参数，其实只是做了封装。

from sklearn.model_selection import GridSearchCV
param_grid = [
    {
        'weights': ['distance'],
        'n_neighbors': [i for i in range(2, 11)],
        'p': [i for i in range(1, 6)]
    }
]
grid_search = GridSearchCV(knn_clf, param_grid, verbose=1)
grid_search.fit(X_train, y_train)
grid_search.best_score_                     # 最好的score
grid_search.best_params_                    # 最好的模型参数
best_knn_clf = grid_search.best_estimator_  # 最好的模型的实例
best_knn_clf.score(X_test, y_test)