Landau-Vishkin

基础算法

假设我们有两个字符串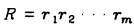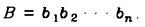：，每个字符串由A C G T四个字母组成。

在两个字符串上，都有三种可能的编辑操作（突变）：

1. 删除某个字符
2. 在某个位置插入字符
3. 改变某个字符

每一个编辑操作都有惩罚值。用D(R,B)表示字符串R和B的最小编辑距离(总惩罚值)。

在这里，我们将三种编辑操作的惩罚值都设为1。

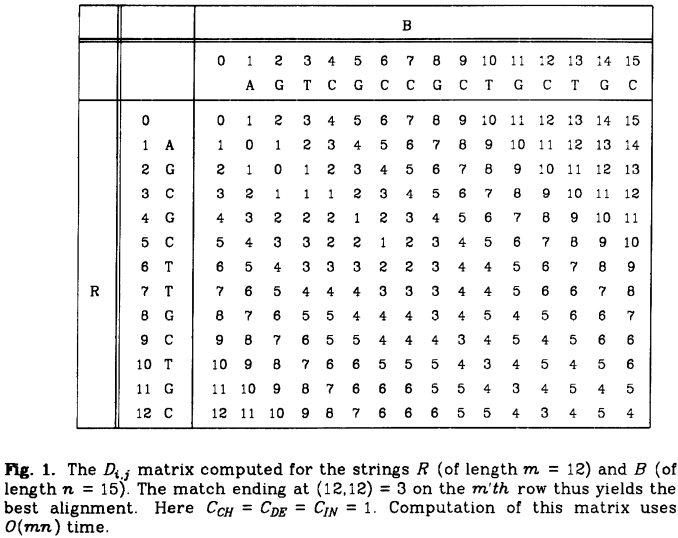
定义矩阵D，X维和Y维分别表示字符串B和R。在矩阵的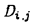上，我们尝试对两个字符串对应位置的字符进行匹配，并计算相应位置的分数。

在矩阵上DP的过程实际上具有生物学意义。比如，上下或者左右移动意味着插入或者删除，在对角线上移动意味着匹配/失配。

很明显，在对角线上移动比左右/上下移动更容易找到符合条件的匹配。

示例图片：

伪代码：

算法优化

上面的算法的时间复杂度为O(m^2)。

在上一个算法的推导过程中，我们可以发现：在矩阵上DP的过程中，偏离中心对角线很远的元素基本不会符合答案要求。

设k为最大的惩罚值，通过限制搜索过程中D中元素的大小，只要大于k就放弃该元素，就可以达到优化时间复杂度到O(km)的效果。

在此基础上，考虑能否通过优化DP矩阵的两个维度，通过直接限制搜索空间的方法将空间复杂度也优化到O(km)。

可以发现，一个比较好的匹配总是沿对角线进行的。而且，如果遍历每一条对角线，一定能找到最终匹配。

定义差异值e(e<=k)作为新矩阵的一个维度。考虑到算法基础是以对角线为中心，向两边拓展差异值<=k，那么对角线编号应当作为矩阵的另一个维度。

我们将计算的矩阵重新定义为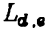,其中d代表第几个对角线，e代表当前差异值。

可以发现，目前缺少一个代表"位于对角线的哪个位置"的元素。那么，就将元素值设为当前位于模式串的第几个字符，也就是之前D矩阵的行数即可。

现在，L矩阵上元素的值指对于第d个对角线，在差异值为e的情况下，最多能拓展到第几行。

接下来，考虑如何计算这个矩阵。

思考对角线之间的关系，可以发现：对于任意一条对角线，可以通过其相邻两条对角线当前拓展到的最大行数+1更新这一条对角线能拓展到的最大行数。这是因为通过一个插入/删除操作可以使两条相邻对角线上的对齐转化到当前对角线上。

因此，对于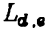，只有

• 位于同一条对角线且差异值比他小1的元素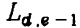+1
• 在上面的一条对角线上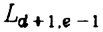， +1
• 在下面的一条对角线上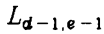，+1

可以更新它的值。

伪代码

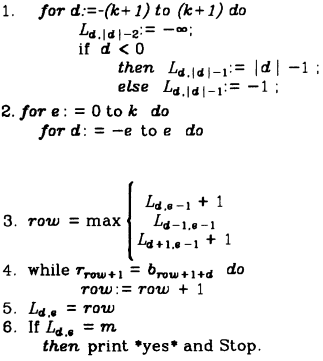
C++代码

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<map>
const int INF = 20000000;
const int MAXN = 2000;
const int MAXK = 100;

void setValue(int L[MAXN][MAXK], int i, int j, int value) {
    L[i + (MAXN >> 1)][j + (MAXK >> 1)] = value;
}

int getValue(int L[MAXN][MAXK], int i, int j) {
    return L[i + (MAXN >> 1)][j + (MAXK >> 1)];
}

bool sameChar(char r[], char b[], int rIndex, int bIndex,int lenB,int lenR) {
    rIndex--;
    bIndex--;
    if (rIndex == 0 && bIndex == 0)return 1;
    if (rIndex < 0 || bIndex < 0) {
        printf("WRONG!");
        return 0;
    }
    if (rIndex >= lenR || bIndex >= lenB)return 0;
    return r[rIndex] == b[bIndex];
}

bool isSame(char r[], char b[],int lenB,int lenR) {
    if (lenR != lenB)return 0;
    for (int i = 0; i < lenR; i++) {
        if (r[i] != b[i])return 0;
    }
    return 1;
}

void printAll(int L[MAXN][MAXK], int k) {
    // 第几个对角线
    for (int i = -k; i <= k; i++) {
        // 差异值
        for (int j = -k; j <= k; j++) {
            printf("L[%d][%d]=%d ", i, j, getValue(L, i, j));
        }
        printf("\n");
    }
}

void init(int L[MAXN][MAXK], char r[], char b[], int k) {
    for (int d = -(k + 1); d <= k + 1; d++) {
        setValue(L, d, abs(d) - 2, -INF);
        if (d < 0) {
            setValue(L, d, abs(d) - 1, abs(d) - 1);
        } else {
            setValue(L, d, abs(d) - 1, -1);
        }
    }
}

#define scanf_s scanf

int max(int a,int b){
    if(a>b)return a;
    return b;
}

int main() {
    // 两个字符串
    char r[MAXN], b[MAXN];

    int k;

    int dp[MAXN][MAXK];
    memset(dp, 0, sizeof(dp));

    printf("R Input:");
    scanf_s("%s", &r);
    printf("B Input:");
    scanf_s("%s", &b);
    printf("k:");
    scanf_s("%d", &k);
    init(dp, r, b, k);

    int lenB=strlen(b);
    int lenR=strlen(r);

    if (k == 0) {
        if (isSame(r, b,lenB,lenR)) {
            printf("yes\n");
        } else {
            printf("no\n");
        }
        return 0;
    }

    // 遍历每一个差异值
    for (int e = 0; e <= k; e++) {
        // 遍历每一个差异值的所有对角线
        for (int d = -e; d <= e; d++) {
            int row = max(getValue(dp, d, e-1) + 1,
                max(getValue(dp, d - 1, e - 1), getValue(dp, d + 1, e - 1) + 1));
            while (sameChar(r, b, row + 1, row + 1 + d,lenB,lenR)) {
                row++;
            }
            setValue(dp, d, e, row);
            if (getValue(dp, d, e) == lenR) {
                printf("yes\n");
                //printAll(dp, k);
                return 0;
            }
        }
    }

    //printAll(dp, k);
    printf("no\n");
    return 0;
}

对拍

数据生成

#include<cstdio>
#include<iostream>
#include<cmath>
#include<string>
#include<algorithm>
#include<ctime>
#include<map>
const int INF = 20000000;
const int MAXN = 2000;
using namespace std;

int min(int a,int b){
    if(a<b)return a;
    return b;
}

string randomChar(){
    int opt=rand()%4;
        switch(opt){
            case 0:
                return "A";
            case 1:
                return "T";
            case 2:
                return "C";
            case 3:
                return "G";
        }
}

string createSequence(string str,int len){
    for(int i=0;i<len;i++){
        str+=randomChar();
    }
    return str;
}

string insert(string str){
    int len=str.length();
    int index=rand()%len;
    return str.insert(index,randomChar());
} 

string replace(string str){
    int len=str.length();
    int index=rand()%len;
    char oldChar=str[index];
    while(oldChar==str[index]){
        str=str.replace(index,1,randomChar());
    }
    return str;
}

string _delete(string str){
    int len=str.length();
    int index=rand()%len;
    return str.erase(index,1);
}

string randomOpt(string origin,int optNum){
    string tmp=origin;
    for(int i=1;i<=optNum;i++){
        int opt=rand()%3;
        switch(opt){
            case 0:
                tmp=insert(tmp);
                continue;
            case 1:
                tmp=replace(tmp);
                continue;
            case 2:
                tmp=_delete(tmp);
                continue;
        }
    }
    return tmp;
}

int main() {
    srand((int)time(NULL));
    int len=rand()%10+5;
    int optNum=rand()%(min(40,len-3));
    string b="",r="";
    b=createSequence(b,len);
    r=randomOpt(b,optNum);

    int is=rand()%2;
    int delta=rand()%3;
    if(is==0){
        delta*=-1;
    }

    if(r.length()>b.length()){
        printf("%s\n",b.c_str());
        printf("%s\n",r.c_str());
        printf("%d\n",optNum+delta);
    }else{
        printf("%s\n",r.c_str());
        printf("%s\n",b.c_str());
        printf("%d\n",optNum+delta);
    }

    return 0;
}

正确代码

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<map>
const int INF = 20000000;
const int MAXN = 2000;

void printAll(int dp[MAXN][MAXN],int lenR,int lenB) {
    for (int i = 0; i <= lenR; i++) {
        for (int j = 0; j <= lenB; j++) {
            printf("%d ", dp[i][j]);
        }
        printf("\n");
    }
}

int min(int a,int b){
    if(a<b)return a;
    return b;
}

int dp[MAXN][MAXN];
int main() {
    // 涓や釜瀛楃涓?
    char r[MAXN], b[MAXN];
    int k;

    printf("R Input:");
    scanf("%s", &r);
    printf("B Input:");
    scanf("%s", &b);
    printf("k:");
    scanf("%d", &k);

    int lenR = strlen(r), lenB = strlen(b);
    dp[0][0] = 0;
    for (int j = 1; j <= lenB; j++) {
        dp[0][j] = j;
    }
    for (int i = 1; i <= lenR; i++) {
        dp[i][0] = i;
    }
    for (int i = 1; i <= lenR; i++) {
        for (int j = 1; j <= lenB; j++) {
            int tmp = dp[i - 1][j - 1];
            if (r[i - 1] != b[j - 1])tmp++;
            dp[i][j] = min(dp[i - 1][j] + 1, min(dp[i][j - 1] + 1, tmp));
        }
    }
    int minn=INF;
    for (int i = 1; i <= lenB; i++) {
        minn = min(minn, dp[lenR][i]);
    }
    // printAll(dp, lenR, lenB);
    if (minn <= k) {
        printf("yes\n");
    }else {
        printf("no\n");
    }
    return 0;
}