COGS 2581 无聊的会议V2

传送

题目大意

给定一个长为\(n\)的序列,定义\(y\)在三元对\((x,y,z)\)中成为中心轴当且仅当同时满足:\(a_x = a_y = a_z,y-x=z-y,x<y<z\)对于每个位置\(i\)求使\(i\)成为中心轴的三元对的数量.

题解

首先我们发现\((a_i \leq 5)\)所以我们可以分别枚举0~5这6个数字

假设当前枚举到\(num\)，那么把等于\(num\)的置为1,其余的置为0

那么现在问题转化成了怎么求出值全为1的三元对

观察下图:假设方框所选作为中心轴



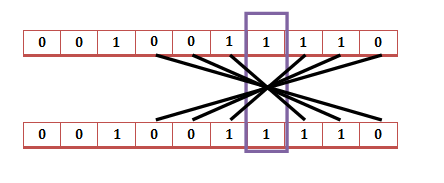
则中心轴的数量+1当且仅当黑线的两端均为1

我们发现若黑线表示两数相乘,那么乘法运算恰好符合上一句

并且我们发现这构成了卷积的形式

所以我们使用FFT加速

由数学知识可以得到,以i为中心轴的三元对个数储存于\(2i\)中

但是因为我们计算时没有保证\(x < z\)所以不要忘了\(ans/=2\)

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
inline void read(int &x){
	x=0;char ch;bool flag = false;
	while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
	while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
const int maxn = 1048576+1+11424;
const int mod = 23068673;
const int pri_rt = 3;
int e[maxn],ie[maxn],len;
inline int qpow(int x,int p){
	int ret = 1;
	for(;p;x=1LL*x*x%mod,p>>=1) if(p&1) ret=1LL*ret*x%mod;
	return ret;
}
inline void init(int n){
	len = n;
	int bas = qpow(pri_rt,(mod-1)/len);
	int inv = qpow(bas,mod - 2);
	e[0] = ie[0] = 1;
	for(int i=1;i<n;++i){
		e[i] = 1LL*e[i-1]*bas%mod;
		ie[i] = 1LL*ie[i-1]*inv%mod;
	}
}
inline void FNT(int n,int *x,int *w){
	for(int i=0,t=0;i<n;++i){
		if(i > t) swap(x[i],x[t]);
		for(int j=n>>1;(t^=j) < j;j>>=1);
	}
	for(int m=2;m<=n;m<<=1){
		int k = m>>1,t = len/m;
		for(int i=0;i<n;i+=m){
			for(int j=0,p=0;j<k;++j,p+=t){
				int u = 1LL*x[i+j+k]*w[p]%mod;
				x[i+j+k] = x[i+j] - u;
				if(x[i+j+k] < 0) x[i+j+k] += mod;
				x[i+j] += u;
				if(x[i+j] >= mod) x[i+j] -= mod;
			}
		}
	}
	if(w == ie){
		int inv = qpow(n,mod-2);
		for(int i=0;i<n;++i) x[i] = 1LL*x[i]*inv%mod;
	}
}
int a[maxn],c[maxn],ans[maxn];
int main(){
	freopen("OXO.in","r",stdin);
	freopen("OXO.out","w",stdout);
	int n;read(n);
	for(int i=0;i<n;++i) read(a[i]);
	int len;for(int i=1;(i>>2)<n;i<<=1) len = i;
	init(len);
	for(int num=0;num<=5;++num){
		memset(c,0,sizeof c);
		for(int i=0;i<n;++i) if(a[i] == num) c[i] = 1;
		FNT(len,c,e);
		for(int i=0;i<len;++i) c[i] = 1LL*c[i]*c[i]%mod;
		FNT(len,c,ie);
		for(int i=0;i<len;++i){
			if( (i&1) || a[i>>1] != num ) continue;
			if(c[i] < 0) c[i] += mod;
			ans[i>>1] += c[i]>>1;
		}
	}
	for(int i=0;i<n;++i) printf("%d\n",ans[i]);
	getchar();getchar();
	return 0;
}