牛客挑战赛14-F细胞

https://www.nowcoder.com/acm/contest/81/F

循环卷积的裸题，太久没做FFT了，这么裸的循环卷积都看不出来

注意一下本文的mod 都是指表示幂的模数，而不是NTT用到的模数

• 首先我们先不管m,考虑多项式

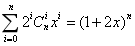
可以发现这个是一个多项式的n次幂，正常求一个多项式的n次幂，可以用快速幂套NTT，复杂度n*log(n)*log(n)， 最多只能做n在1e4左右的题。

• 现在在来考虑m，则原式为。

　　　　　　显然这就是循环卷积的常见形式

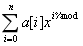
　　　　如果先用快速幂套NTT 把多项式系数算出来a[i]， 再对i%mod同余的系数进行累加，时间和空间都是会爆炸的。

　　不过在多项式快速幂实现的时候不难发现，可以每做一次多项式乘法，就对幂取余一次，合并幂的余数相同的项。这样空间可以降到2*mod, 时间复杂度    mod*log(mod)*log(n)      但是这样还是会超时的

• 最后重点来了，上面是一般的情况的下循环卷积的做法，循环卷积还有一种特殊情况，就是指数的mod=2^m 时，这时循环卷积可以直接变成频域上的2^m-1 次多项式的点乘（注意要系数等于2^m-1 的点乘， 不需要先以前一样开两倍大小，以防止多项式系数溢出，这里就是要溢出才能保证正确性），这时可以发现，NTT 前可NTT后都是mod-1次多项,没有系数合并的那一步，所以干脆中间乘的时候，就不要NTT回来，  直接在点成的时候做快速幂。 这样只需做一次NTT和逆NTT.时间复杂度  mod*(log(n)+log(mod))

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
typedef long long ll;
#define N 2000005
ll a[N],b[N];
const ll PMOD=;
const ll PR=;
static ll qp[];
ll res[N];
struct NTT__container
{
    NTT__container()
    {
        int  t,i;
        for( i=; i<; i++)///注意循环上界与2n次幂上界相同
        {
            t=<<i;
            qp[i]=quick_pow(PR,(PMOD-)/t);
        }
    }
    ll quick_pow(ll x,ll n)
    {
        ll ans=;
        while(n)
        {
            if(n&)
                ans=ans*x%PMOD;
            x=x*x%PMOD;
            n>>=;
        }
        return ans;
    }
    int get_len(int n)///计算刚好比n大的2的N次幂
    {
        int i,len;
        for(i=(<<); i; i>>=)
        {
            if(n&i)
            {
                len=(i<<);
                break;
            }
        }
        return len;
    }
    inline void NTT(ll F[],int len,int type)
    {
        int id=,h,j,k,t,i;
        ll E,u,v;
        for(i=,t=; i<len; i++)///逆位置换
        {
            if(i>t)    swap(F[i],F[t]);
            for(j=(len>>); (t^=j)<j; j>>=);
        }
        for( h=; h<=len; h<<=)///层数
        {
            id++;
            for( j=; j<len; j+=h)///遍历这层上的结点
            {
                E=;///旋转因子
                for(int k=j; k<j+h/; k++)///遍历结点上的前半序列
                {
                    u=F[k];///A[0]
                    v=(E*F[k+h/])%PMOD;///w*A[1]
                    ///对偶计算
                    F[k]=(u+v)%PMOD;
                    F[k+h/]=((u-v)%PMOD+PMOD)%PMOD;
                    ///迭代旋转因子
                    E=(E*qp[id])%PMOD;///qp[id]是2^i等分因子
                }
            }
        }
        if(type==-)
        {
            int i;
            ll inv;
            for(i=; i<len/; i++)///转置，因为逆变换时大家互乘了对立点的因子
                swap(F[i],F[len-i]);
            inv=quick_pow(len,PMOD-);///乘逆元还原
            for( i=; i<len; i++)
                F[i]=(F[i]%PMOD*inv)%PMOD;
        }
    }
    inline void inv(ll *a,int len)///答案存在res中
    {
        if(len==)
        {
            res[]=quick_pow(a[],PMOD-);
            return ;
        }
        inv(a,len>>);///递归
        static ll temp[N];
        memcpy(temp,a,sizeof(ll)*(len>>));
        NTT(temp,len,);
        NTT(res,len,);
        int i;
        for(i=; i<len; i++)
            res[i]=res[i]*(-temp[i]*res[i]%PMOD+PMOD)%PMOD;///多项式逆元迭代公式
        NTT(res,len,-);
        memset(res+(len>>),,sizeof(ll)*(len>>));
    }
    void mul(ll x[],ll y[],int len)///答案存在x中
    {
        int i;
        NTT(x,len,);///先变换到点值式
        NTT(y,len,);///先变换到点值式上
        for(i=; i<len; i++)
            x[i]=(x[i]*y[i])%PMOD;///在点值上点积
        NTT(x,len,-);///再逆变换回系数式
    }

} cal;
void print(ll a[],int len)
{
    int high=,i;
    for(i=len-; i>=; i--)
    {
        if(a[i])
        {
            high=i;
            break;
        }
    }
    for(i=high; i>=; i--)putchar(a[i]+'');
    puts("");
}
int main()
{
    int m,i,j,k,len;
    long long n;
//    printf("%lld\n",PMOD);
    scanf("%lld%d",&n,&m);
    len=<<m;
    a[]=;
    a[]=;
    cal.NTT(a,len,);
    for(i=;i<len;i++)
    {
        a[i]=cal.quick_pow(a[i],n);
    }
    cal.NTT(a,len,-);
    long long temp=,ans=;
    for(i=;i<len;i++)
    {
        ans+=temp*a[i]%PMOD;
        temp=temp*%PMOD;
    }
    printf("%lld\n",ans%PMOD);
    return ;
}