哈夫曼树：HDU5884-Sort（队列、哈夫曼树）

Sort

Time Limit: 3000/1000 MS (Java/Others)

Memory Limit: 32768/32768 K (Java/Others)

题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5884

Problem Description

Recently, Bob has just learnt a naive sorting algorithm: merge sort. Now, Bob receives a task from Alice.

Alice will give Bob N sorted sequences, and the i-th sequence includes ai elements. Bob need to merge all of these sequences. He can write a program, which can merge no more than k sequences in one time. The cost of a merging operation is the sum of the length of these sequences. Unfortunately, Alice allows this program to use no more than T cost. So Bob wants to know the smallest k to make the program complete in time.

Input

The first line of input contains an integer t0, the number of test cases. t0 test cases follow.

For each test case, the first line consists two integers N (2≤N≤100000) and T (∑Ni=1 ai < T < 231).

In the next line there are N integers a1,a2,a3,…,aN(∀i,0≤ai≤1000).

Output

For each test cases, output the smallest k.

Sample Input

1

5 25

1 2 3 4 5

Sample Output

3

---

解题心得：

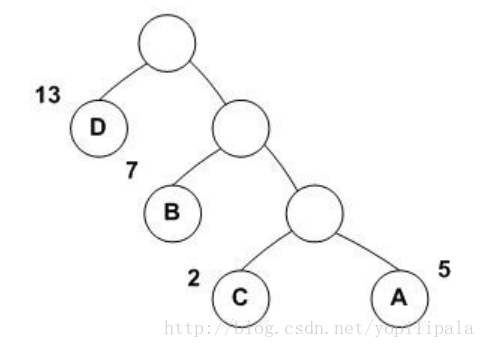
1. 可以看出是一个k叉的哈夫曼树，确定k值的时候只能使用二分法。
2. 要写k叉的哈夫曼树要克服几个条件，首先给出的数目不符合一个哈夫曼树的时候要填充0来凑数，然后一般写哈夫曼树都是使用优先队列，但是这个题卡掉了优先队列，可以根据合并的有序性来优化，使用两个队列，每次比较队顶元素的大小，取小的就行。
3. 凑零的个数公式是：k - 1 - (n - 1)%(k - 1)。可以根据这个哈夫曼树的图来了解。
   
   

---

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
vector <ll> ve;
queue <ll> qu,qu2;
bool checke(ll mid,ll m,ll n)
{
    while(!qu.empty())
        qu.pop();
    while(!qu2.empty())
        qu2.pop();
    ll ans = 0;
    /*如果当前的数目不可以直接得到一个哈夫曼数的时候可以
    添加权值为0的根节点来充凑*/
    if((n - 1)%(mid - 1) != 0)
    {
        ll k = (n - 1)%(mid - 1);
        for(int i=0;i<mid-1-k;i++)
            qu.push(0);
    }
    for(int i=0;i<ve.size();i++)
        qu.push(ve[i]);
    /*可以根据合并的单调性用两个队列来优化时间，优化后的
    时间是O(nlogn);
    如果使用优先队列的复杂度会达到O(n(logn)^2);
    */
    while(!qu.empty() || !qu2.empty())
    {
        ll sum = 0;
        for(int i=0;i<mid;i++)
        {
            if(qu.empty() && qu2.empty())
                break;
            if(qu.empty())
            {
                sum += qu2.front();
                qu2.pop();
            }
            else if(qu2.empty())
            {
                sum += qu.front();
                qu.pop();
            }
            else
            {
                ll a = qu2.front();
                ll b = qu.front();
                if(a < b)
                {
                    sum += a;
                    qu2.pop();
                }
                else
                {
                    sum += b;
                    qu.pop();
                }
            }
        }
        ans += sum;
        if(qu.empty() && qu2.empty())
            break;
        qu2.push(sum);
    }
    if(ans > m)
        return true;
    return false;
}

void solve(ll n,ll m)
{
    ll r,mid,l;
    r = n,l = 0;
    while(l < r)
    {
        mid = (l + r) / 2;
        if(checke(mid,m,n))
            l = mid+1;
        else
            r = mid;
    }
    printf("%lld\n",l);
}

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        ve.clear();
        ll n,m;
        scanf("%lld%lld",&n,&m);
        ll N = n;
        while(N--)
        {
            ll temp;
            scanf("%lld",&temp);
            ve.push_back(temp);
        }
        sort(ve.begin(),ve.end());
        solve(n,m);
    }
}