主成分分析（PCA）与SVD奇异值分解

 

主要参考：https://www.zhihu.com/question/38417101/answer/94338598

http://blog.jobbole.com/88208/

先说下PCA的主要步骤：
假设原始数据是10（行，样例数，y1-y10）*10（列，特征数x1-x10）的（10个样例，每样例对应10个特征）
（1）、分别求各特征（列）的均值并对应减去所求均值。

（2）、求特征协方差矩阵。<img src="https://pic2.zhimg.com/cc03314fa1a36dc02e16ebb42385e331_b.png" data-rawwidth="462" data-rawheight="215" class="origin_image zh-lightbox-thumb" width="462" data-original="https://pic2.zhimg.com/cc03314fa1a36dc02e16ebb42385e331_r.png">

对角线上是方差，非对角线是协方差；协方差为0时两者独立，其绝对值越大，两者对彼此的影响越大。
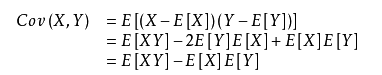
（3）、求协方差阵的特征值和特征向量。
（4）、将特征值按照从大到小排序，选择其中最大的k个。将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
（5）、将样本点投影到选取的k个特征向量上。这里需要捋一捋，若原始数据中样例数为m，特征数为n，减去均值后的样本矩阵仍为MatrixDATA(m,n); 协方差矩阵是C（n,n）;特征向量矩阵为EigenMatrix(n,k); 投影可得： FinalDATA(m,k)=MatrixDATA(m,n) * EigenMatrix(n,k) 。
这样，原始数据就由原来的n维特征变成了k维，而k维数据是原数据的线性组合。

作者：Hana
链接：https://www.zhihu.com/question/38417101/answer/94338598
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

下面需要把特征协方差阵和投影单独拎出来说一下：
1、为什么求特征协方差的特征向量就是最理想的k维向量？
2、投影的过程意义在于？

【对于第一点】 可以通过最大方差理论解释。处理信号时，信噪比定义为10倍lg信号与噪声功率之比，这个用非周期的数字信号平均功率来解释比较直观（模拟信号只要做积分即可），在观测时间序列有N个时间点，将每个时间点的幅值的平方作和，再将总和除以点数N，信噪比其实就是信号与噪声的方差比。而一般认为，信号具有较大的方差（包含信息），噪声具有较小的方差。所以我们认为的最好的k个特征应该尽可能的包含有用信号，亦即信号损失尽可能小。故在将n维特征转换为k维后，取的是前k个较大方差的特征方向。下面 我们来看一下投影的详细过程（图片引自JerryLead blog）
<img src="https://pic1.zhimg.com/2d91f456c0c6e6661979ceb684952f90_b.png" data-rawwidth="504" data-rawheight="352" class="origin_image zh-lightbox-thumb" width="504" data-original="https://pic1.zhimg.com/2d91f456c0c6e6661979ceb684952f90_r.png">u是直线的斜率也是直线的方向向量，而且是u是直线的斜率也是直线的方向向量，而且是单位向量。样本点x在u上的投影点距离远点的距离是两向量内积，

这里u为单位向量，故内积即为投影的长度。
考虑m个样本点都做u上的投影，故样本在u上投影后的点的方差（只考虑u方向，参照原点）可以计算如下：

前面样本点经过预处理，每一维特征均值为0，故投影到u上的样本点（只有一个到原点的距离值）的均值仍然是0。方差计算如下
<img data-rawwidth="367" data-rawheight="134" src="https://pic4.zhimg.com/ba5b7495e4645991bcf24532d0f57757_b.png" class="content_image" width="367">

u为单位向量，中间部分
<img src="https://pic1.zhimg.com/1e1af9db7d50566fec4b550dc6e3984c_b.png" data-rawwidth="116" data-rawheight="54" class="content_image" width="116">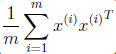其实相当于样本的特征协方差矩阵，这里我要详细的解释一下为什么。

还记得样本的特征协方差矩阵吗？特征协方差矩阵中非对角线元素的求法为cov(x1,x2) = E{[(x1-E(x1)][x2-E(x2)]}，也就是两个特征所对应的样本值序列分别减去各自均值后的乘积的均值（因为是无偏估计，这里计算均值是除以m-1而非m）。
理一理我们手头上的数据： m个样例； n个特征<img src="https://pic3.zhimg.com/df43c1f76c7e0cacc6c0394af8aad222_b.png" data-rawwidth="159" data-rawheight="27" class="content_image" width="159">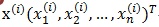
在求特征协方差矩阵时的x1,x2,....xn是对应的特征列。是Data中的列，这里不要和行

<img src="https://pic3.zhimg.com/df43c1f76c7e0cacc6c0394af8aad222_b.png" data-rawwidth="159" data-rawheight="27" class="content_image" width="159">搞混淆哦，如果我们要求特征x1的方差D（x1)=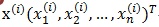搞混淆哦，如果我们要求特征x1的方差D（x1)=; 特征x1,x2的协方差Cov(x1,x2)= 。其余以此类推。再看<img src="https://pic1.zhimg.com/1e1af9db7d50566fec4b550dc6e3984c_b.png" data-rawwidth="116" data-rawheight="54" class="content_image" width="116">注意这里最为重要，需要理解。 公式中是列向量与行向量的乘积（结果是一个矩阵），对m个矩阵做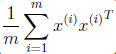注意这里最为重要，需要理解。 公式中是列向量与行向量的乘积（结果是一个矩阵），对m个矩阵做结果是一个矩阵。我们不妨试着将这个矩阵乘开看一看是什么鬼。

我们再来看下面的推导：

用表示,表示 .那么式子=就可以写成：

u是单位向量，,对 式两边左乘u有，也就是

；是我们的特征协方差矩阵，故也就是该矩阵的特征值u就是特征向量。故=的最大值就是 的最大值，也就是的最大值。

PCA最终保留的前k个特征值就是对应的前k大的方差的特征方向。

【对于第二点】 可以看到投影过程为： FinalDATA(m,k)=MatrixDATA(m,n) * EigenMatrix(n,k)

试思考：1，矩阵右乘列向量-- 得到新的列向量为矩阵各列的线性组合
2，矩阵A右乘矩阵B（k列）-- 得到新的矩阵，该矩阵每一列均为A矩阵各列做k次不同的线性组合的结果。这也就是楼上说的新的特征（k列）是原特征（n列）线性组合的结果。如果非要看新的k维是原来的特征如何得到的，可以把特征协方差矩阵的特征向量求取出来，对应看出如何做的线性组合。
关于线性组合与投影：为什么投影可以用线性组合或者说是矩阵相乘来实现呢？
这里涉及坐标空间的变换，把数据从原空间投影到选择的k维特征空间中。这里解释起来比较多，姑且就理解为一种线性映射吧，有时间再来补充。实际上k<n故
把数据从原空间投影到选择的k维特征空间中会损失掉一部分的信息（后n-k个特征向量对应的信息），这也是主成分分析降维的结果。

 

 

奇异值与主成分分析（PCA）：

主成分分析在上一节里面也讲了一些，这里主要谈谈如何用SVD去解PCA的问题。PCA的问题其实是一个基的变换，使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量，我们在讲一个东西的稳定性的时候，往往说要减小方差，如果一个模型的方差很大，那就说明模型不稳定了。但是对于我们用于机器学习的数据（主要是训练数据），方差大才有意义，不然输入的数据都是同一个点，那方差就为0了，这样输入的多个数据就等同于一个数据了。以下面这张图为例子：

这个假设是一个摄像机采集一个物体运动得到的图片，上面的点表示物体运动的位置，假如我们想要用一条直线去拟合这些点，那我们会选择什么方向的线呢？当然是图上标有signal的那条线。如果我们把这些点单纯的投影到x轴或者y轴上，最后在x轴与y轴上得到的方差是相似的（因为这些点的趋势是在45度左右的方向，所以投影到x轴或者y轴上都是类似的），如果我们使用原来的xy坐标系去看这些点，容易看不出来这些点真正的方向是什么。但是如果我们进行坐标系的变化，横轴变成了signal的方向，纵轴变成了noise的方向，则就很容易发现什么方向的方差大，什么方向的方差小了。

一般来说，方差大的方向是信号的方向，方差小的方向是噪声的方向，我们在数据挖掘中或者数字信号处理中，往往要提高信号与噪声的比例，也就是信噪比。对上图来说，如果我们只保留signal方向的数据，也可以对原数据进行不错的近似了。

PCA的全部工作简单点说，就是对原始的空间中顺序地找一组相互正交的坐标轴，第一个轴是使得方差最大的，第二个轴是在与第一个轴正交的平面中使得方差最大的，第三个轴是在与第1、2个轴正交的平面中方差最大的，这样假设在N维空间中，我们可以找到N个这样的坐标轴，我们取前r个去近似这个空间，这样就从一个N维的空间压缩到r维的空间了，但是我们选择的r个坐标轴能够使得空间的压缩使得数据的损失最小。

还是假设我们矩阵每一行表示一个样本，每一列表示一个feature，用矩阵的语言来表示，将一个m * n的矩阵A的进行坐标轴的变化，P就是一个变换的矩阵从一个N维的空间变换到另一个N维的空间，在空间中就会进行一些类似于旋转、拉伸的变化。

而将一个m * n的矩阵A变换成一个m * r的矩阵，这样就会使得本来有n个feature的，变成了有r个feature了（r < n)，这r个其实就是对n个feature的一种提炼，我们就把这个称为feature的压缩。用数学语言表示就是：

但是这个怎么和SVD扯上关系呢？之前谈到，SVD得出的奇异向量也是从奇异值由大到小排列的，按PCA的观点来看，就是方差最大的坐标轴就是第一个奇异向量，方差次大的坐标轴就是第二个奇异向量…我们回忆一下之前得到的SVD式子：

在矩阵的两边同时乘上一个矩阵V，由于V是一个正交的矩阵，所以V转置乘以V得到单位阵I，所以可以化成后面的式子

将后面的式子与A * P那个m * n的矩阵变换为m * r的矩阵的式子对照看看，在这里，其实V就是P，也就是一个变化的向量。这里是将一个m * n 的矩阵压缩到一个m * r的矩阵，也就是对列进行压缩，如果我们想对行进行压缩（在PCA的观点下，对行进行压缩可以理解为，将一些相似的sample合并在一起，或者将一些没有太大价值的sample去掉）怎么办呢？同样我们写出一个通用的行压缩例子：

这样就从一个m行的矩阵压缩到一个r行的矩阵了，对SVD来说也是一样的，我们对SVD分解的式子两边乘以U的转置U’

这样我们就得到了对行进行压缩的式子。可以看出，其实PCA几乎可以说是对SVD的一个包装，如果我们实现了SVD，那也就实现了PCA了，而且更好的地方是，有了SVD，我们就可以得到两个方向的PCA，如果我们对A’A进行特征值的分解，只能得到一个方向的PCA。