【动态规划】bzoj1584: [Usaco2009 Mar]Cleaning Up 打扫卫生

思路自然的巧妙dp

Description

有N头奶牛，每头那牛都有一个标号Pi，1 <= Pi <= M <= N <= 40000。现在Farmer John要把这些奶牛分成若干段，定义每段的不河蟹度为：若这段里有k个不同的数，那不河蟹度为k*k。那总的不河蟹度就是所有段的不河蟹度的总和。

Input

第一行：两个整数N，M

第2..N+1行：N个整数代表每个奶牛的编号

Output

一个整数，代表最小不河蟹度

Sample Input

13 4
1
2
1
3
2
2
3
4
3
4
3
1
4

Sample Output

11

---

题目分析

$O(n^2)$的dp不难得到，即$f_i=min\{f_j+w(j+1,i)\}$.

旁敲侧击

分析一下数据范围，会想到做法大概是$O(nlogn)$或者$O(n\sqrt n)$的。

一开始还往决策单调性的方向想，然而发现颜色个数的平方这个加权并没有决策单调性……

看了题解才发现，是一种思路自然的神奇$O(n\sqrt n)$dp……

$O(n\sqrt n)$dp

考虑答案的下界，即每一个元素单独成组，答案是$n$.这意味着在最优解中，每组颜色个数必然是小于等于$\sqrt n$的。从这个性质出发，可以记$[pos[j],i]$为以$i$为右端点、颜色个数小于等于$j$的最长序列。

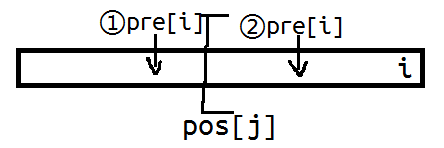
那么就是如何维护$pos[j]$.这个和其他统计颜色的问题类似，记$pre[i],lst[i]$分别为与$a_i$同色的前、后一个位置；$cnt[j]$为当前$pos[j]$的不同颜色数量。那么每当新加进一个元素$i$的时候，就看一下$pre[i]$在$pos[j]$之前还是之后，并根据这个信息维护$pos[j]$的右移。

所以虽然根据答案上界来限定枚举颜色数量的这一步比较难想，后面的过程还是非常巧妙自然的。

 #include<bits/stdc++.h>
 const int maxn = ;
 const int maxk = ;

 int n,m,size;
 int a[maxn],nxt[maxn],pre[maxn],lst[maxn],f[maxn],pos[maxk],cnt[maxk];

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch=getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch=getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 void Min(int &x, int y){x = x<y?x:y;}
 int main()
 {
     memset(f, 0x3f3f3f3f, sizeof f);
     n = read(), m = read(), size = sqrt(n+0.5), f[] = ;
     for (int i=; i<=size; i++) pos[i] = ;
     for (int i=; i<=n; i++)
     {
         a[i] = read();
         pre[i] = lst[a[i]], nxt[lst[a[i]]] = i;
         lst[a[i]] = i, nxt[i] = n+;
     }
     for (int i=; i<=n; i++)
         for (int j=; j<=size; j++)
         {
             if (pre[i] < pos[j]) cnt[j]++;
             if (cnt[j] > j){
                 cnt[j]--;
                 while (nxt[pos[j]] < i) pos[j]++;
                 pos[j]++;
             }
             Min(f[i], f[pos[j]-]+1ll*j*j);
         }
     printf("%d\n",f[n]);
     return ;
 }

END