【BZOJ4407】于神之怒加强版 莫比乌斯反演

【BZOJ4407】于神之怒加强版

Description

给下N,M,K.求

Input

输入有多组数据，输入数据的第一行两个正整数T,K，代表有T组数据，K的意义如上所示，下面第二行到第T+1行，每行为两个正整数N,M，其意义如上式所示。

Output

如题

Sample Input

1 2
3 3

Sample Output

20

HINT

1<=N,M,K<=5000000,1<=T<=2000

题解：如何快速推出线性筛的递推式呢？——打表。

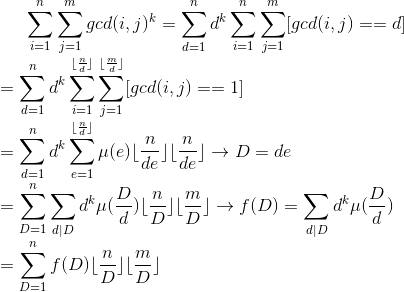
发现f(D)长得跟$\varphi（D）$差不多？所以递推式也差不多

$f(i*pj)=\begin{cases}& f(i)*(pj^k-1) & i\%pj!=0 \\ & f(i)*pj^k & i\%pj==0\end{cases}$

#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
const int N=5000000;
int T,k,num;
int pri[N];
ll f[N+10],sf[N+10],pk[N],ans;
bool np[N+10];
ll pm(ll x,ll y)
{
	ll z=1;
	while(y)
	{
		if(y&1)	z=z*x%mod;
		x=x*x%mod,y>>=1;
	}
	return z;
}
void init()
{
	int i,j;
	f[1]=sf[1]=1;
	for(i=2;i<=N;i++)
	{
		if(!np[i])	pri[++num]=i,pk[num]=pm(i,k),f[i]=pk[num]-1;
		sf[i]=sf[i-1]+f[i];
		for(j=1;j<=num&&i*pri[j]<=N;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)
			{
				f[i*pri[j]]=f[i]*pk[j]%mod;
				break;
			}
			f[i*pri[j]]=f[i]*(pk[j]-1)%mod;
		}
	}
}
void work()
{
	int n,m,i,last;
	ans=0;
	scanf("%d%d",&n,&m);
	if(n>m)	swap(n,m);
	for(i=1;i<=n;i=last+1)
	{
		last=min(n/(n/i),m/(m/i));
		ans=(ans+(sf[last]-sf[i-1])*(n/i)%mod*(m/i)%mod)%mod;
	}
	printf("%lld\n",(ans+mod)%mod);
}
int main()
{
	scanf("%d%d",&T,&k);
	init();
	while(T--)	work();
	return 0;
}