HT for Web 3D游戏设计设计--汉诺塔（Towers of Hanoi）

在这里我们将构造一个基于HT for Web的HTML5+JavaScript来实现汉诺塔游戏。

汉诺塔的游戏规则及递归算法分析请参考http://en.wikipedia.org/wiki/Tower_of_Hanoi。

知道了汉诺塔的规则和算法，现在就开始创建元素。用HT for Web（http://www.hightopo.com）现有的3D模板创建底盘和3根柱子不是问题，问题是要创建若干个中空的圆盘。一开始的想法是：创建一个圆柱体，将圆柱体的上下两端隐藏，设置柱面的宽度来实现圆盘的效果，经过多次尝试并查阅相关api文档，发现柱面是没有厚度的，改方法不可行。

后来在HT for Web自定义3D模型的WebGL应用（http://www.hightopo.com/blog/381.html）受到启发，圆盘的形成就是在xy平面上的一个矩形，根据y轴旋转一周产生的，通过查阅相关文档，最总决定采用ht.Default.createRingModel方法来创建圆盘模型，然后在创建node的时候通过shape3d属性引用创建好的模型。

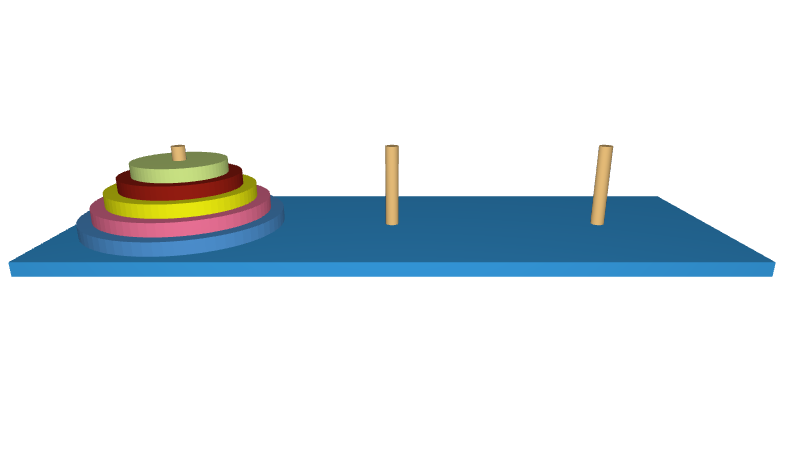
在逻辑实现上，采用了栈的先进后出的原理，对圆柱上的圆盘做顺序控制，确保每次移动的圆盘都是最小的圆盘。

在算法上，采用的是递归算法，通过递归算法，将搬迁过程一步一步记录下来，再采用堆的原理一步一步地执行搬迁过工作。

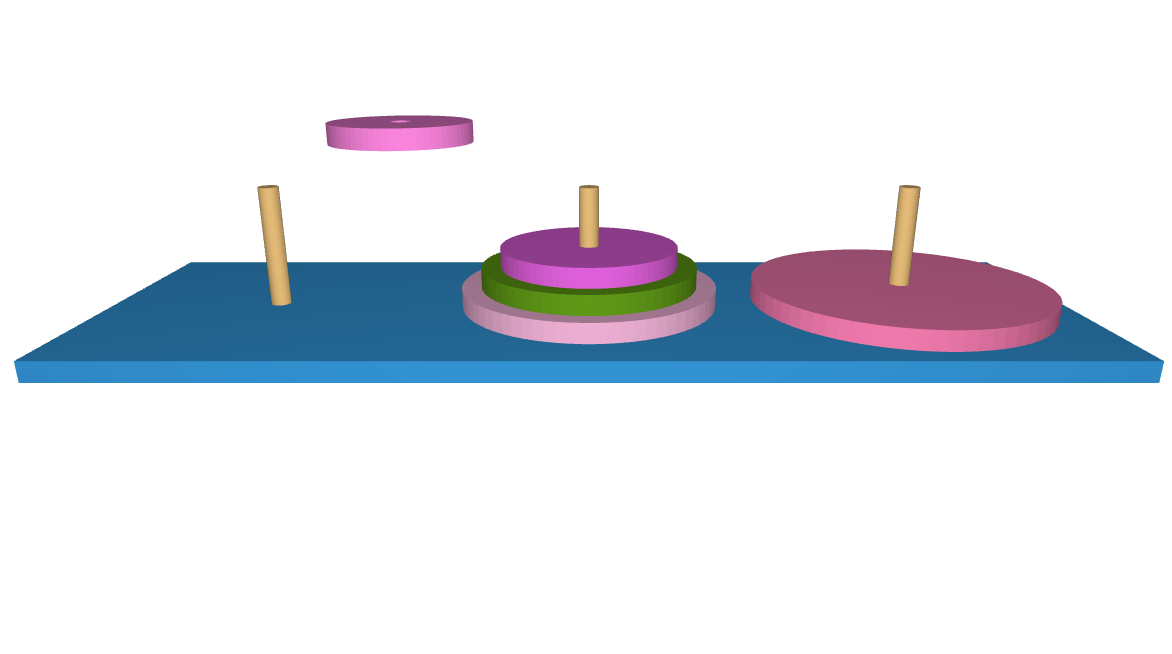
http://v.youku.com/v_show/id_XODcwMTk4MDI4.html

var barNum = 5, // 圆盘个数
    cylinderHeight = barNum * 20 + 40, // 圆柱高度
    barrelMinORadius  = 50, // 圆盘最大外半径
    barrelIRadius = 10, // 圆盘内半径
    poorRadius = 20, // 圆盘外半径差值
    barrelMaxORadius = barrelMinORadius + barNum * poorRadius,
    barrelHeight = 20, // 圆盘高
    barPadding = 20, // 柱体之间的间隙
    floorX = barrelMaxORadius * 6 + barPadding * 4, // 底盘长
    floorY = 20, // 底盘高
    floorZ = 2 * barrelMaxORadius + barPadding * 2, // 底盘宽
    // 柱体集
    positions = [
        {
            barrels: [],
            position: [-(2*barrelMaxORadius + barPadding), cylinderHeight / 2 + 1, 0]
        },{
            barrels: [],
            position: [0, cylinderHeight / 2 + 1, 0]
        },{
            barrels: [],
            position: [(2*barrelMaxORadius + barPadding), cylinderHeight / 2 + 1, 0]
        }
    ],
    runOrder = [], // 圆盘移动顺序集
    // 动画参数
    params = {
        delay: 10,
        duration: 500,
        easing: Easing['easeBoth']
    };

/**
 * 初始化程序
 * */
function init(){
    dataModel = new ht.DataModel();
    g3d = new ht.graph3d.Graph3dView(dataModel);
    view = g3d.getView();
    view.className = 'main';
    document.body.appendChild(view);
    window.addEventListener('resize', function (e) {
        g3d.invalidate();
    }, false);

    g3d.setEye([0, cylinderHeight * 2, floorX * sin(2*PI/360*60)]);

    // 初始化节点
    initNodes();

    moveAnimation();
}

/**
 * 构造游戏移动队列
 * diskQuantity：圆盘个数
 * positionA：起点
 * positionB：中转点
 * positionC：终点
 * */
function buildRunOrder(diskQuantity, positionA, positionB, positionC){
    if (diskQuantity == 1) {
        runOrder.push([positionA, positionC]);
    } else {
        buildRunOrder(diskQuantity - 1, positionA, positionC, positionB);
        buildRunOrder(1, positionA, positionB, positionC);
        buildRunOrder(diskQuantity - 1, positionB, positionA, positionC);
    }
}

/**
 * 移动动画
 * positionA：起点
 * positionC：终点
 * */
function moveAnimation(positionA, positionC){
    if(!positionA){
        var poses = runOrder.shift();
        if(!poses){
            setTimeout(reset, 500);
        }else{
            moveAnimation(positions[poses[0]], positions[poses[1]]);
        }
    }else {
        var barrel = positionA.barrels.pop();
        var position = positionC.cylinder.p3(),
            barPos = barrel.getPosition3d();
        position[1] = position[1] + floorY + barrelHeight * positionC.barrels.length - cylinderHeight / 2;
        setPolylinePoints(polyline, barPos, position);
        params.action = function (v, t) {
            var length = g3d.getLineLength(polyline),
                offset = g3d.getLineOffset(polyline, length * v),
                point = offset.point,
                px = point.x,
                py = point.y,
                pz = point.z;
            barrel.p3(px, py, pz);
        };
        params.finishFunc = function () {
            positionC.barrels.push(barrel);
            var poses = runOrder.shift();
            if (!poses) {
                moveAnimation();
            } else {
                moveAnimation(positions[poses[0]], positions[poses[1]]);
            }
        };
        anim = ht.Default.startAnim(params);
    }
}

/**
 * 重置游戏
 * */
function reset(){
    if(positions[0].barrels.length == 0){
        positions[0].barrels = positions[2].barrels;
    }
    positions[2].barrels = [];
    for(var i = 0, len = positions[0].barrels.length; i < len; i++){
        var pos = positions[0].cylinder.p3();
        pos[1] = pos[1] + floorY + i * barrelHeight - cylinderHeight / 2;
        positions[0].barrels[i].p3(pos);
    }
    buildRunOrder(barNum, 0, 1, 2);
    setTimeout(moveAnimation, 500);
}

/**
 * 初始化节点
 * */
function initNodes(){
    // 底盘
    floor = createNode([0, floorY / 2, 0], [floorX, floorY, floorZ]).s({
        'shape3d':  'box',
        '3d.movable': false
    });

    // 创建柱子
    for(var i = 0, len = 3; i < len; i++){
        positions[i].cylinder = createNode(positions[i].position, [20, cylinderHeight, 20], floor).s({
            'shape3d':  'cylinder',
            'shape3d.color': '#E5BB77',
            '3d.movable': false
        });
    }

    // 创建圆盘
    createBarrels(barNum, positions[0].cylinder);

    // 创建圆盘运行轨迹
    polyline = new ht.Polyline();
    polyline.setSegments([1, 2, 4, 2]);
    polyline.s({
        'shape.background': null,
        'shape.border.color': 'rgba(0,0,0,0)',
        'shape.border.gradient.color': 'rgba(0,0,0,0)',
        'shape.border.pattern': [20, 10],
        'shape3d.resolution': 50
    });
    dataModel.add(polyline);
}

/**
 * 设置路线节点
 * */
function setPolylinePoints(polyline, from, to){
    polyline.setPoints([
        {x: from[0], y: from[2], e: from[1]},
        {x: from[0], y: from[2], e: cylinderHeight},
        {x: from[0], y: from[2], e: cylinderHeight + 60},
        {x: to[0], y: to[2], e: cylinderHeight + 60},
        {x: to[0], y: to[2], e: cylinderHeight},
        {x: to[0], y: to[2], e: to[1]}
    ]);
    return polyline;
}

/**
 * 创建圆盘
 * barNum：圆盘个数
 * host：吸附节点
 * */
function createBarrels(barNum, host){
    // 圆盘初始x位置
    var pos = host.p3();

    for(var i = barNum, j = 0; i > 0; i--, j++){
        pos[1] = barrelHeight * j + floorY;
        positions[0].barrels.push(createBarrel(pos, [1, barrelHeight, 1], barrelMinORadius + i*poorRadius, barrelIRadius, host).s({
            'shape3d.color': randomColor(),
            '3d.movable': false
        }));
    }
}

/**
 * 创建节点
 * p3：节点位置
 * s3：节点大小
 * host：吸附节点
 * */
function createNode(p3, s3, host){
    var node = new ht.Node();
    node.p3(p3);
    node.s3(s3);
    node.setHost(host);
    node.s({
        'wf.visible': 'selected',
        'wf.color': '#FF6B10',
        'wf.width': 2,
        'wf.short': true
    });
    dataModel.add(node);
    return node;
}

/**
 * 创建空心圆柱
 * p3：圆桶位置
 * s3：圆桶大小
 * oRadius：圆桶外径
 * iRadius：圆桶内径
 * host：吸附节点
 * */
function createBarrel(p3, s3, oRadius, iRadius, host){
    return createNode(p3, s3, host).s({
        'shape3d':  ht.Default.createRingModel([
            oRadius, 1,
            oRadius, 0,
            iRadius, 0,
            iRadius, 1,
            oRadius, 1
        ], null, 20, false, false, 70)
    });
}