(惊艳)基于谷底最小值的阈值的图像分割（改进HSV中的H分量可以用imhist(H)提取）

任务概述:将这张图片作为输入 ， 然后抠出只有斑点的图片

灵感来源：

1. 黄色部分用绿色的掩盖掉得到图片B，然后A和B进行∩运算，相同的设置为0

2.统计单词的子母数，开辟一个26个元素的数组，进来一个字母在相应的地方++，类似hashmap

3.为什么要用Hue这个分量下手，因为这幅图就2个颜色，肯定会在2个地方突出来，然后中间的波谷

作为分隔点，其中一个突出来的部分置为0

4.Hue分量在[0,1]连续 变化 ， 灰度值和R分量在【0,255】离散的变化，将【0,1】线性变化到【0,255】

R分量就像是随机变量X，自身只能离散的取值 ， H分量是double类型的，取值是连续的

I=imread('375.png');

hv=rgb2hsv(I);    %自带的函数就是good
H=hv(:,:,1);
S=hv(:,:,2);
V=hv(:,:,3);     %也可以分别绘制H,S,V分量的图片

[M,N,D] = size(I);
vec = zeros(1,256) %初始化一个256元素的行矩阵

for i=1:M
	for j=1:N
            if(  round( H(i,j)*255 ) == 0 )
          　　　　 array(1,1) = array(1,1) +0 ;  

         %       if(  round( H(i,j)*255 )==257 )
         %         array(1,256) = array(1,256) +1 ;
       else
           vec( 1 , round( H(i,j)*255 ) ) = vec( 1 , round( H(i,j)*255 ) ) + 1; %见备注图片   %改进自带的函数
       end
    end
end

%写入
Mat = array ;
fid = fopen('D:\data.txt','wt');
[row,col] = size(Mat);
for i=1 : row
    for j = 1:col
	fprintf(fid,'%g\n',Mat(i,j)); %换行
    end
end
fclose(fid);

　　

  

---

H_hist = imhist(H)          将451*235个值映射到[0,1]区间有多少（将H分量的所有取值映射到[0.255]这256个离散的点上：最精辟理解啊）

那个3段算法中也是将[0,x1]的任一一个点  映射到[0,y1]    这是一对一映射 ，上面那个是多对一映射

---

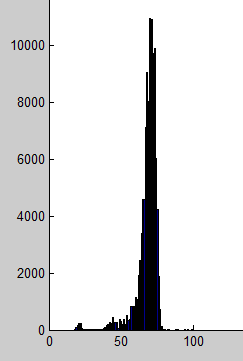
假设得到阈值（最后介绍方法） 44

这一步是将大于阈值的点统统处理掉

num = 44/255.0; %手动修改
[M,N] = size(H);

for i=1:M
　　for j=1:N
      if( H(i,j) > num ) % 绿色部分显然要多些
	   V(i,j) = 0; 
　　　　end; %V分量0是白色
    end
end

V2 = V;
temp = cat(3,H,S,V2);
temp = hsv2rgb(temp);
imshow(temp);

　　

实现--基于谷底最小值的阈值

1、描述：

　　此方法实用于具有明显双峰直方图的图像，其寻找双峰的谷底作为阈值，但是该方法不一定能获得阈值，对于那些具有平坦的直方图或单峰图像，该方法不合适。

　　2、实现过程：

　　该函数的实现是一个迭代的过程，每次处理前对直方图数据进行判断，看其是否已经是一个双峰的直方图，如果不是，则对直方图数据进行半径为1（窗口大小为3）的平滑，如果迭代了一定的数量比如1000次后仍未获得一个双峰的直方图，则函数执行失败，如成功获得，则最终阈值取两个双峰之间的谷底值作为阈值。

注意在编码过程中，平滑的处理需要当前像素之前的信息，因此需要对平滑前的数据进行一个备份。另外，首数据类型精度限制，不应用整形的直方图数据，必须转换为浮点类型数据来进行处理，否则得不到正确的结果。

知乎上还有人求这个判断双峰的算法

package erer;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.Arrays;

public class test {

	public static int GetMinimumThreshold(int[] HistGram) {
		int Y, Iter = 0;
		double[] HistGramC = new double[256]; // 基于精度问题，一定要用浮点数来处理，否则得不到正确的结果
		double[] HistGramCC = new double[256]; // 求均值的过程会破坏前面的数据，因此需要两份数据
		for (Y = 0; Y < 256; Y++) {
			HistGramC[Y] = HistGram[Y];
			HistGramCC[Y] = HistGram[Y];
		}

		// 通过三点求均值来平滑直方图
		while (IsDimodal(HistGramCC) == false) // 判断是否已经是双峰的图像了
		{
			HistGramCC[0] = (HistGramC[0] + HistGramC[0] + HistGramC[1]) / 3; // 第一点
			for (Y = 1; Y < 255; Y++)
				HistGramCC[Y] = (HistGramC[Y - 1] + HistGramC[Y] + HistGramC[Y + 1]) / 3; // 中间的点
			HistGramCC[255] = (HistGramC[254] + HistGramC[255] + HistGramC[255]) / 3; // 最后一点
			// // System.Buffer.BlockCopy(HistGramCC, 0, HistGramC, 0, 256 *
			// sizeof(double));

			System.arraycopy(HistGramCC, 0, HistGramC, 0, 256);

			Iter++;
			if (Iter >= 1000)
				return -1; // 直方图无法平滑为双峰的，返回错误代码
		}
		// 阈值极为两峰之间的最小值
		boolean Peakfound = false;
		for (Y = 1; Y < 255; Y++) {
			if (HistGramCC[Y - 1] < HistGramCC[Y] && HistGramCC[Y + 1] < HistGramCC[Y])
				Peakfound = true;
			if (Peakfound == true && HistGramCC[Y - 1] >= HistGramCC[Y] && HistGramCC[Y + 1] >= HistGramCC[Y])
				return Y - 1;
		}
		return -1;
	}

	private static boolean IsDimodal(double[] HistGram) // 检测直方图是否为双峰的
	{
		// 对直方图的峰进行计数，只有峰数位2才为双峰
		int Count = 0;
		for (int Y = 1; Y < 255; Y++) {
			if (HistGram[Y - 1] < HistGram[Y] && HistGram[Y + 1] < HistGram[Y]) {
				Count++;
				if (Count > 2)
					return false;
			}
		}
		if (Count == 2)
			return true;
		else
			return false;
	}

	public static void main(String args[]) throws IOException {

		File file = new File("D:\\data.txt");// Text文件
		BufferedReader br = new BufferedReader(new FileReader(file));// 构造一个BufferedReader类来读取文件
		String s = null;
		int[] data1 = new int[256];
		int i = 0;
		while ((s = br.readLine()) != null) {// 使用readLine方法，一次读一行

			// System.out.println(s);
			System.out.println("--------------");
			try {
				String str = s;
				String str2 = str.replaceAll(" ", "");
				System.out.println(str2);
				data1[i] = Integer.parseInt(str2);
				;
				i++;
			} catch (NumberFormatException e) {
				e.printStackTrace();
			}
			System.out.println(Arrays.toString(data1));
			System.out.println(data1.length);

		}
		br.close();
		;

		int[] HistGram = new int[256];

		System.arraycopy(data1, 0, HistGram, 0, 256);

		int num = GetMinimumThreshold(HistGram);

		System.out.println("阈值是" + num);
	}
}

　　

得到阈值是28，运行