线性代数笔记13——Ax=b的通解

　　关于最简行阶梯矩阵和矩阵秩，可参考《线性代数笔记7——再看行列式与矩阵》

　　召唤一个方程Ax = b：

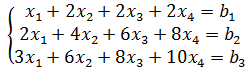
　　3个方程4个变量，方程组有无数解，现在要关注的是b₁b₂b₃之间满足什么条件时方程组有解，它的解是什么？

　　在这个例子中可以马上看出，b₁+b₂ = b₃，一般的方法是消元法化简：

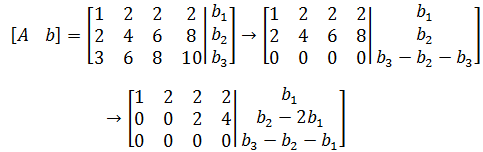
　　化简到这一步就可以确定主元是x₁和x₃。通过最后一行可知，b₃ – b₂ - b₁ = 0。b₁b₂b₃可以是任意数，所以只要满足b₃ – b₂ - b₁ = 0，方程组就有解。这样的组合很多，可以很容易找到一个特解：

　　现在我们知道了b中三个分量的关系，并且还知道只有当 b属于A的列空间时有解。通过上一章的方法可知，列空间的基就是主元所在的列：

　　到此为止回答了第一个问题，什么样的b才能使Ax = b有解。现在需要回答另一个问题，Ax = b的所有解是什么？

　　可以先找出一个特解，方法是令所有自由元为0，然后解出主元：

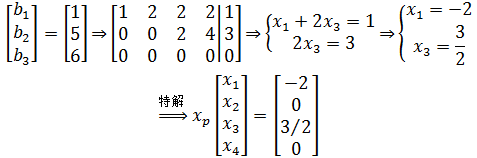
　　已经找到了一个特解，那么方程组的其它解，也就是通解是什么呢？

　　假设Ax= 0的零空间的任意向量是x_n，Ax = b有一个特解x_p，那么有：

　　二者相加：

　　所以方程组的通解是x_n + x_p。对于方程组的某解x_p来说，x_p与零空间内任意向量之和仍为解。现在看看零空间：

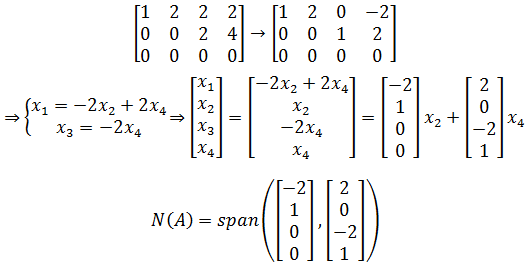
　　综合特解，得到Ax = b的通解：

　　矩阵的秩和主元个数相同。如果A是一个m行n列的矩阵，其主元的个数一定小于m，并且也小于n。如果A的每一列都有主元，那么A是满秩矩阵，没有自由元，如果此时有解，则解是唯一的，就是特解，即x = x_p，此时不需要求解零空间，零空间只包含零向量。

---

作者：我是8位的

出处：http://www.cnblogs.com/bigmonkey

本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！

扫描二维码关注公众号“我是8位的”