一步一步写数据结构(二叉树的建立和遍历,c++)
简述:
二叉树是十分重要的数据结构,主要用来存放数据,并且方便查找等操作,在很多地方有广泛的应用。
二叉树有很多种类,比如线索二叉树,二叉排序树,平衡二叉树等,本文写的是最基础最简单的二叉树。
思路:
二叉树的建立采用的是递归的思想:给定一个指向根节点的指针,然后递归调用ceate()函数,自动生成一个二叉树。就像是在地上挖了个坑(根节点),然后他会拿着铲子(create函数)按照一定的规则自动挖一个很大的洞穴(二叉树)出来。当然挖坑前需要先定义每个洞长什么样(定义节点结构)。
二叉树的遍历采用的也是递归的思想:如果节点有数据,则按照遍历规则打印根节点和孩子节点,没有数据则返回直到所有数据都遍历完,递归结束。
不废话,上代码:
#include<iostream>
using namespace std; //定义节点
typedef struct node
{
struct node *lchild;
struct node *rchild;
char data;
}BiTreeNode, *BiTree; //*BiTree的意思是给 struct node*起了个别名,叫BiTree,故BiTree为指向节点的指针。 //按照前序顺序建立二叉树
void createBiTree(BiTree &T) //&的意思是传进来节点指针的引用,括号内等价于 BiTreeNode* &T,目的是让传递进来的指针发生改变
{
char c;
cin >> c;
if('#' == c) //当遇到#时,令树的根节点为NULL,从而结束该分支的递归
T = NULL;
else
{
T = new BiTreeNode;
T->data=c;
createBiTree(T->lchild);
createBiTree(T->rchild);
}
} //前序遍历二叉树并打印
void preTraverse(BiTree T)
{
if(T)
{
cout<<T->data<<" ";
preTraverse(T->lchild);
preTraverse(T->rchild);
}
}
//中序遍历二叉树并打印
void midTraverse(BiTree T)
{
if(T)
{
midTraverse(T->lchild);
cout<<T->data<<" ";
midTraverse(T->rchild);
}
}
//后续遍历二叉树并打印
void postTraverse(BiTree T)
{
if(T)
{
postTraverse(T->lchild);
postTraverse(T->rchild);
cout<<T->data<<" ";
}
}
int main()
{
BiTree T; //声明一个指向二叉树根节点的指针
createBiTree(T);
cout<<"二叉树创建完成!"<<endl;
cout<<"前序遍历二叉树:"<<endl;
preTraverse(T);
cout<<endl;
cout<<"中序遍历二叉树:"<<endl;
midTraverse(T);
cout<<endl;
cout<<"后序遍历二叉树:"<<endl;
postTraverse(T);
return ;
}
测试结果:
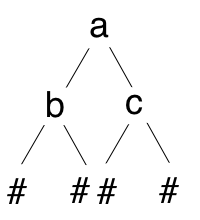
假设我们要建立一个如下图所示的二叉树,#代表空节点,按照前序遍历顺序二叉树表示为:ab##c##
. 
下面是代码的运行结果,正如预期:
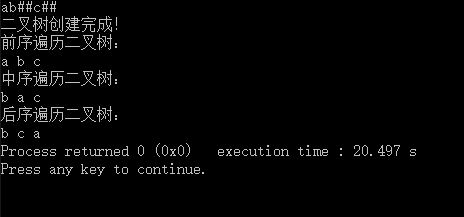
一步一步写数据结构(二叉树的建立和遍历,c++)的更多相关文章
- C语言二叉树的建立与遍历
二叉树的建立和遍历都要用到递归,先暂时保存一下代码,其中主要是理解递归的思想,其它的就都好理解了.这里是三种遍历方式,其实理解一种,其它的几个就都理解了,就是打印出来的顺序不一样而已.建立和遍历的方式 ...
- 二叉树的建立以及遍历的多种实现(python版)
二叉树是很重要的数据结构,在面试还是日常开发中都是很重要的角色. 首先是建立树的过程,对比C或是C++的实现来讲,其涉及到了较为复杂的指针操作,但是在面向对象的语言中,就不需要考虑指针, 内存等.首先 ...
- 二叉树的建立与遍历(c语言)入门
树其实在本质上就是一对多,链表就是一对一. 二叉树的建立: 这里的代码采用的是最粗暴的创建方法,无实际用处.但初次学习二叉树可以通过这个创建方法更好的理解二叉树. 二叉树的遍历: 遍历在大体上分为递归 ...
- C语言实现二叉树的建立、遍历以及表达式的计算
实现代码 #include <stdio.h> #include <stdlib.h> #include <malloc.h> #include <ctype ...
- 二叉树的建立与遍历(山东理工OJ)
题目描写叙述 已知一个按先序序列输入的字符序列,如abc,,de,g,,f,,,(当中逗号表示空节点).请建立二叉树并按中序和后序方式遍历二叉树,最后求出叶子节点个数和二叉树深度. 输入 输入一个长度 ...
- python实现二叉树的建立以及遍历(递归前序、中序、后序遍历,队栈前序、中序、后序、层次遍历)
#-*- coding:utf-8 -*- class Node: def __init__(self,data): self.data=data self.lchild=None self.rchi ...
- 一步一步写平衡二叉树(AVL树)
平衡二叉树(Balanced Binary Tree)是二叉查找树的一个进化体,也是第一个引入平衡概念的二叉树.1962年,G.M. Adelson-Velsky 和 E.M. Landis发明了这棵 ...
- 一步一步写算法(之prim算法 下)
原文:一步一步写算法(之prim算法 下) [ 声明:版权所有,欢迎转载,请勿用于商业用途. 联系信箱:feixiaoxing @163.com] 前两篇博客我们讨论了prim最小生成树的算法,熟悉 ...
- 一步一步写算法(之prim算法 上)
原文:一步一步写算法(之prim算法 上) [ 声明:版权所有,欢迎转载,请勿用于商业用途. 联系信箱:feixiaoxing @163.com] 前面我们讨论了图的创建.添加.删除和保存等问题.今 ...
随机推荐
- Spring+SpringMVC+Mybatis整合(二)
目录结构:
- WPF复制异常问题(OpenClipboard 失败 (异常来自 HRESULT:0x800401D0 (CLIPBRD_E_CANT_OPEN)))
最近在维护WPF系统的时候发现的问题,刚刚开始自己的电脑都不能重现,后面写日志跟踪才发现问题的所在.问题主要是由于:1. 在程序访问剪切板的时候,有其他程序正在占用剪切板,导致自己的程序无法访问, ...
- UML和模式应用5:细化阶段(4)--如何创建领域模型
1.前言 以当前迭代中所要设计的需求为界,创建领域模型的步骤: 1.寻找概念类 2.将其绘制为UML类图中的类 3.添加关联和属性 2.如何寻找概念类 寻找概念类有如下几种方法: 重用和修改现有的模型 ...
- Shell 中test 单中括号[] 双中括号[[]] 的区别
Shell test 单中括号[] 双中括号[[]] 的区别 在写Shell脚本的时候,经常在写条件判断语句时不知道该用[] 还是 [[]],首先我们来看他们的类别: $type [ [[ test ...
- (常用)subprocess模块 详情官方
subprocess包中定义有数个创建子进程的函数,这些函数分别以不同的方式创建子进程,所以我们可以根据需要来从中选取一个使用.另外subprocess还提供了一些管理标准流(standard str ...
- Nodejs 实现ESL内联FreeSWITCH设定说明
一.背景说明: SIP Server IP (Centos):192.168.11.61 ,服务器IP(Windows):192.168.11.19 二.目的: 能够从192.168.11.19上通 ...
- 实现div里的内容垂直居中
---恢复内容开始--- 在项目中我们会遇到这种情况,一个div的宽固定,里面的内容长度不定,不管是一行还是多行,都要垂直居中,有俩个实现方法: 1.使用absolute,top:50%,transf ...
- OCM_第十天课程:Section5—》数据仓库
注:本文为原著(其内容来自 腾科教育培训课堂).阅读本文注意事项如下: 1:所有文章的转载请标注本文出处. 2:本文非本人不得用于商业用途.违者将承当相应法律责任. 3:该系列文章目录列表: 一:&l ...
- php中foreach()跳出循环或者终止循环的实现方法
$arr = array('a','b','c','d','e'); $html = ''; foreach($arr as $key => $value){ if($value=='b'){ ...
- web----框架基础
Web框架本质: 众所周知,对于所有的Web应用,本质上其实就是一个socket服务端,用户的浏览器其实就是一个socket客户端. 真实开发中的python web程序来说,一般会分为两部分:服务器 ...
