Unity3D学习笔记（三十三）：矩阵

矩阵

矩阵就是一行和列组织起来的矩形数字块。

矩阵可以理解为是向量的数组。

 

矩阵的维度和记法

矩阵的维度是包含多少行多少列！例如1行2列的矩阵

记法：矩阵m中，对于第1行第2列的元素，我们记为m12

 

方阵

行数和列数相同的矩阵，我们叫做方阵。一般情况下，我们研究的就是2x2, 3x3, 4x4的方阵

 

对角线元素

方阵中，行号和列号相同的元素就是对角线元素，其他的都是非对角线元素。

 

单位矩阵

对角线元素都为1，非对角线元素都为0的矩阵

 

转置矩阵

对于矩阵M，M的转置矩阵MT，

MT就是把M的行变为列，把M的列变成行

 

向量和矩阵

行向量：一行几列的矩阵

列向量：几行一列的矩阵

 

矩阵的运算：

标量和矩阵的乘法：

M = m11 m12 * 2 = 2*m11 2*m12

        m21 m22          2*m21 2*m22

矩阵中的每一个元素都与这个标量相乘，最终结果还是一个矩阵。

 

矩阵与矩阵相乘：

矩阵和矩阵的乘法，并不是什么形式都可以，必须让左边矩阵的列和右边矩阵的行保持一致，否则不能相乘。

矩阵与矩阵相乘的结果：还是一个矩阵，该矩阵的行数是左边矩阵的行数，该矩阵的列数就是右边矩阵的列数。

矩阵与矩阵相乘，不满足乘法交换律。

 

对于结果矩阵中的Cij

Cij = 左边矩阵的第i行的每个元素与右边矩阵的第j列的每个元素相乘的和。

  -
  -
-   

a b c d f
g h i j k

k
 k 

1x- + -2x4, 1x7 + -2x1/
5x- + 0x4, 5x7 + 0x1/

3x- + -1x0 + 4x3, 3x0 + -1x7 + 4x-, 3x3 + -1x- + 4x2,

2x2 + 3x5 +4x3, 2x3 + 3x7 +4x4, 2x1 + 3x2 +4x5
2x2 + 7x5 +10x3, 2x3 + 7x7 +10x4, 2x1 + 7x2 +10x5

向量和矩阵的乘法

行向量：放在矩阵的左侧进行乘运算，左乘矩阵

列向量：放在矩阵的右侧进行乘运算，右乘矩阵

对于同一个向量同一个矩阵，这个向量左乘矩阵的结果，与右乘矩阵的结果不一致！

 

矩阵的几何意义：

对于给定的向量a，矩阵M，有aM = b,，那么我们可以说M将a转换到了b，那么一个向量乘以一个矩阵相当于做了一次坐标变换。

 

描述一个物体变换时的规律。

其中包括：旋转，缩放，投影，镜像等。

线性变换：从几何上来理解：变换前是直线，变换后依旧是直线，变换前是几何原点，那么变换后依旧是几何原点。如3x3

仿射变换：线性变换 + 平移，如4x4

 

矩阵的行列式（只存在于方阵中）

行列式不是矩阵，是一个标量（就是数）f

方阵的行列式：|M| 或 detM

 

二阶方阵的行列式的计算：

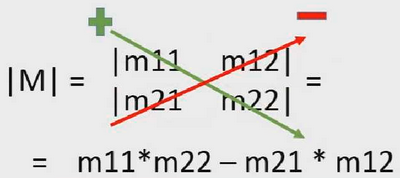
三阶方阵的行列式的计算：

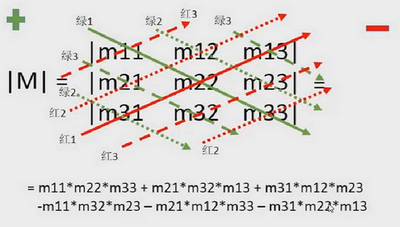
2x2x8+ 3x5x1 + 7x3x3
-2x5x3 - 3x3x8 - 7x2x1

2x5 - 3x4

代数余子式：

代数余子式是数，对于n阶方阵，代数余子式：n*n个

对于n阶方阵中的每个元素都有一个代数余子式。

Cij = 去掉了第i行第j列，剩下的矩阵的行列式 * -1的 i+j 次幂。

矩阵

C11 =(4x2 - 3x1 ) x (-)(+)
C12 =(3x2 - 5x1 ) x (-)(+)
C13 =(3x3 - 5x4 ) x (-)(+)
C21 =(4x2 - 3x5 ) x (-)(+)
C22 =(2x2 - 5x5 ) x (-)(+)
C23 =(2x3 - 5x4 ) x (-)(+)
C31 =(4x1 - 4x5 ) x (-)(+)
C32 =(2x1 - 3x5 ) x (-)(+)
C33 =(2x4 - 3x4 ) x (-)(+)

 -  -
 -
- - -

标准伴随矩阵

对于矩阵M，M的标准伴随矩阵记做adjM

adjM = 就是M矩阵的代数余子式组成矩阵的转置矩阵。

 

矩阵的逆：

方阵的M的逆，记做：M-1

对于矩阵来说，并不是所有的矩阵都有逆矩阵。

如果一个矩阵的行列式不为0，证明这个矩阵是由逆矩阵，可逆的。

如果一个矩阵的行列式为0，证明这个矩阵是不可逆的。

对于一个有逆矩阵的矩阵来说，我们叫做该矩阵是可逆的或非奇异的。

对于一个没有逆矩阵的矩阵来说，该矩阵是不可逆的或奇异的。

 

逆矩阵 = 标准伴随矩阵 / 矩阵的行列式

 

求逆矩阵：

1.求矩阵的行列式，判断矩阵是否可逆

2.求矩阵的标准伴随矩阵（代数余子式组成矩阵的转置矩阵）

3.求逆矩阵

矩阵

矩阵的行列式
|M| =  -  = -

标准伴随矩阵
 -
- 

转置矩阵
 -
- 

逆矩阵
-/ /
/ -/ 

矩阵

矩阵的行列式
|M| = ++ --- = -

标准伴随矩阵
 -
-
  -

转置矩阵
 -
-
  -

逆矩阵
-/ /
/ -/ -/
-/ -/ /

逆矩阵的几何意义：对于M矩阵实现的变换，M的逆矩阵表示的就是相反的变换。

 

旋转矩阵：

 

X' = (Cosθ，Sinθ)

Y' = (-Sinθ，Cosθ)

 

2D旋转变换的矩阵

组成矩阵

Cosθ  Sinθ

-Sinθ  Cosθ

 

如果旋转角为45度

0.707 0.707

-0.707 0.707 

 

对于坐标(1, 0)

0.707 0.707

-0.707 0.707 * (1, 0) = (0.707,0.707)，代表绕着Z轴旋转45度的变换

 

3D旋转变换的矩阵

绕X轴旋转的矩阵（左乘）：

1    0    0

0    Cosθ    Sinθ

0    -Sinθ    Cosθ

绕Y轴旋转的矩阵

Cosθ    0     -Sinθ

0          1     0

Sinθ     0     Cosθ   

绕Z轴旋转的矩阵

Cosθ    Sinθ    0

-Sinθ    Cosθ    0

0    0     1

 

(1, 2, 0)，绕Z轴旋转30度

0.866  0.5  0

-0.5  0.866  0

0  0  1

 

x = 1x0.866 + 2x-5 + 0x0 = 

y = 1x0.5 + 2x0.866 + 0x0 =

z = 1x0 + 2x0 + 0x1 =

 

缩放矩阵：

对于给定的向量(X, Y)，缩放X轴缩放Sx倍，Y轴缩放Sy倍

最终结果是(X*Sx, Y*Sy)

 

            m11 m12

(X, Y) * m21 m22

→

X1 = X*m11 + Y*m21

Y1 = X*m12 + Y*m22

→

X1 = X*Sx

Y1 = Y*Sy

→

X*Sx= X*m11 + Y*m21

Y*Sy= X*m12 + Y*m22

→

m11 = Sx  m12 = 0

m21 = 0    m22 = Sy

 

最终的2D的缩放矩阵

Sx  0

0   Sy

 

最终的3D的缩放矩阵

Sx  0  0

0  Sy  0

0  0  Sz 

Sx 对应的是X的值的缩放系数

Sy 对应的是Y的值的缩放系数

Sz 对应的是Z的值的缩放系数

缩放系数为1的时候，表示没有缩放

 

投影矩阵：

对于XY的投影矩阵（把Z的坐标变为0，其他两个不变）

1  0  0

0  1  0

0  0  0

 

对于XZ平面的投影矩阵

1  0  0

0  0  0

0  0  1

 

对于YZ平面的投影矩阵

0  0  0

0  1  0

0  0  1

 

镜像矩阵：

对于以YZ平面镜像的矩阵

-1  0  0

0  1  0

0  0  1

 

对于以XZ平面镜像的矩阵

1  0  0

0  -1  0

0  0  1

 

对于以XY平面镜像的矩阵

1  0  0

0  1  0

0  0  -1

 

平移：

对于给定向量（x, y, z）平移一个（x', y', z'）的向量的位置

对于向量表示方向：（x, y, z）

对于向量表示坐标：（x+x', y+y', z+z'）

                    m11  m12  m13

（x, y, z） *  m21  m22  m23

                    m31  m32  m33

X1 = X*m11 + Y*m21 + Z*m31 

Y1 = X*m12 + Y*m22 + Z*m32 

Z1 = X*m13 + Y*m23 + Z*m33

三维坐标不能表示平移

 

齐次坐标

（x, y, z）从三维的矢量变成四维（x, y, z, w）

当 w = 1 时，证明 x, y, z 表示的是点

当 w = 0 时，证明 x, y, z 表示的是方向

                    m11  m12  m13  m14

（x, y, z） *  m21  m22  m23  m24

                    m31  m32  m33  m34

                    m41  m42  m43  m44

 

X1 = X*m11 + Y*m21 + Z*m31 + W*m41

Y1 = X*m12 + Y*m22 + Z*m32 + W*m42 

Z1 = X*m13 + Y*m23 + Z*m33 + W*m43 

W1 = X*m14 + Y*m24 + Z*m34 + W*m44

 

X1 = X*m11 + Y*m21 + Z*m31 + W*m41 = x + x'

→

m11=1; m21=0; m31=0; m41=x';

 

Y1 = X*m12 + Y*m22 + Z*m32 + W*m42  = y + y'

→

m12=0; m22=1; m32=0; m42=y';

 

Z1 = X*m13 + Y*m23 + Z*m33 + W*m43  = z + z'

→

m13=0; m23=0; m33=1; m43=z';

 

W1 = X*m14 + Y*m24 + Z*m34 + W*m44 = w

→

m14=0; m24=0; m34=0; m44=1;

 

使用 4x4 的矩阵表示三维向量的平移（左乘矩阵）

1  0  0  0

0  1  0  0

0  0  1  0

x'  y'  z'  1

这是平移的左乘矩阵

 

使用 4x4 的矩阵表示三维向量的旋转

绕Z轴旋转

Cosθ  Sinθ  0  0

-Sinθ  Cosθ  0  0

0  0  1  0

0  0  0  1

 

复合变换：

Cosθ  Sinθ  0  0

-Sinθ  Cosθ  0  0

0  0  1  0

x'  y'  z'  1

 

对于(0, 0, 0)这个点，沿着x轴平移1个单位，再绕着z轴旋转90度

先平移再旋转的结果(0, 1, 0)

先旋转再平移的结果(1, 0, 0)

 

                       0  1  0  0

                      -1  0  0  0

                       0  0  1  0

(0, 0, 0, 1)  *   -1  0  0  1  =  (1, 0, 0, 1)

 

 

旋转 * 平移 = 复合变化（复合变换要注意顺序）

 Cosθ  Sinθ    0  0         1  0  0  0           Cosθ  Sinθ  0  0

-Sinθ  Cosθ   0  0         0  1  0  0         -Sinθ  Cosθ  0  0 

 0        0        1  0          0  0  1  0           0        0      1  0 

 0        0        0  1   *     x'  y'  z'  1   =    x'        y'     z'  1 

 

案例-动态生成网格

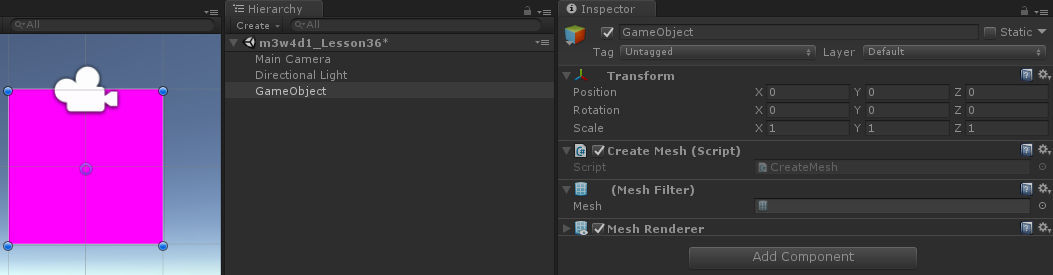
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class CreateMesh : MonoBehaviour
{
       void Start () {

        MeshFilter mf = gameObject.AddComponent<MeshFilter>();
        MeshRenderer mr = gameObject.AddComponent<MeshRenderer>();

        //先实例化一个网格
        Mesh mesh = new Mesh();

        //确定网格的四个顶点
        //先创建一个Vector3类型的数组
        Vector3[] vertexs = new Vector3[];
        vertexs[] = new Vector3(-, , );
        vertexs[] = new Vector3(, , );
        vertexs[] = new Vector3(-, -, );
        vertexs[] = new Vector3(, -, );

        //把顶点给mesh
        mesh.vertices = vertexs;

        //再确定顶点组成三角面的顺序，注意数组的数量一定是3的倍数
        //因为3个顶点才能组成1个三角面，注意三角面的顶点的顺序，顺时针在正面，逆时针在反面
        int[] triangles = new int[] {,,,,,};
        mesh.triangles = triangles;

        //最终把网格给MeshFilter
        mf.mesh = mesh;
    }
}

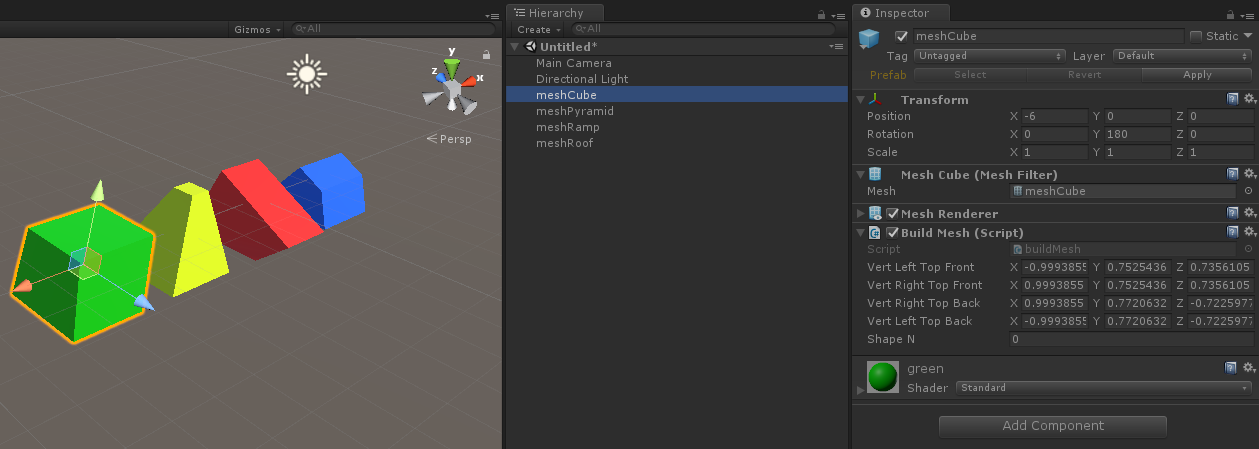
using UnityEngine;
using System.Collections;
public class buildMesh : MonoBehaviour {

       public Vector3 vertLeftTopFront = new Vector3(-,,);
       public Vector3 vertRightTopFront = new Vector3(,,);
       public Vector3 vertRightTopBack = new Vector3(,,-);
       public Vector3 vertLeftTopBack = new Vector3(-,,-);
       private float waitN = 3f;
       private float waitD = 3f;
       public int shapeN = ;

       void Start ()
       {
              MeshFilter mf = GetComponent<MeshFilter>();
              Mesh mesh = mf.mesh;

              //Vertices//
              Vector3[] vertices = new Vector3[]
              {
                     //front face//
                     vertLeftTopFront,//left top front, 0
                     vertRightTopFront,//right top front, 1
                     new Vector3(-,-,),//left bottom front, 2
                     new Vector3(,-,),//right bottom front, 3
                     //back face//
                     vertRightTopBack,//right top back, 4
                     vertLeftTopBack,//left top back, 5
                     new Vector3(,-,-),//right bottom back, 6
                     new Vector3(-,-,-),//left bottom back, 7
                     //left face//
                     vertLeftTopBack,//left top back, 8
                     vertLeftTopFront,//left top front, 9
                     new Vector3(-,-,-),//left bottom back, 10
                     new Vector3(-,-,),//left bottom front, 11
                     //right face//
                     vertRightTopFront,//right top front, 12
                     vertRightTopBack,//right top back, 13
                     new Vector3(,-,),//right bottom front, 14
                     new Vector3(,-,-),//right bottom back, 15
                     //top face//
                     vertLeftTopBack,//left top back, 16
                     vertRightTopBack,//right top back, 17
                     vertLeftTopFront,//left top front, 18
                     vertRightTopFront,//right top front, 19
                     //bottom face//
                     new Vector3(-,-,),//left bottom front, 20
                     new Vector3(,-,),//right bottom front, 21
                     new Vector3(-,-,-),//left bottom back, 22
                     new Vector3(,-,-)//right bottom back, 23
              };

              //Triangles// 3 points, clockwise determines which side is visible
              int[] triangles = new int[]
              {
                     //front face//
                     ,,,//first triangle
                     ,,,//second triangle
                     //back face//
                     ,,,//first triangle
                     ,,,//second triangle
                     //left face//
                     ,,,//first triangle
                     ,,,//second triangle
                     //right face//
                     ,,,//first triangle
                     ,,,//second triangle
                     //top face//
                     ,,,//first triangle
                     ,,,//second triangle
                     //bottom face//
                     ,,,//first triangle
                     ,,//second triangle
              };

              //UVs//
              Vector2[] uvs = new Vector2[]
              {
                     //front face// 0,0 is bottom left, 1,1 is top right//
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,),
                     new Vector2(,)
              };

              mesh.Clear ();
              mesh.vertices = vertices;
              mesh.triangles = triangles;
              mesh.uv = uvs;
              ;
              mesh.RecalculateNormals();

       }

       void Update ()
       {
              if(waitN > 0f)
              {
                     waitN -= Time.deltaTime;
              }
              else
              {
                     waitN = waitD;
                     shapeN ++;
                     if(shapeN > )
                     {
                           shapeN = ;
                     }
              }
              //morph to cube//
              if(shapeN == )
              {
                     vertLeftTopFront = Vector3.Lerp(vertLeftTopFront, new Vector3(-,,),Time.deltaTime);
                     vertRightTopFront = Vector3.Lerp(vertRightTopFront, new Vector3(,,),Time.deltaTime);
                     vertRightTopBack = Vector3.Lerp(vertRightTopBack, new Vector3(,,-),Time.deltaTime);
                     vertLeftTopBack = Vector3.Lerp(vertLeftTopBack, new Vector3(-,,-),Time.deltaTime);
              }
              //morph to pyramid//
              if(shapeN == )
              {
                     vertLeftTopFront = Vector3.Lerp(vertLeftTopFront, new Vector3(,,),Time.deltaTime);
                     vertRightTopFront = Vector3.Lerp(vertRightTopFront, new Vector3(,,),Time.deltaTime);
                     vertRightTopBack = Vector3.Lerp(vertRightTopBack, new Vector3(,,),Time.deltaTime);
                     vertLeftTopBack = Vector3.Lerp(vertLeftTopBack, new Vector3(,,),Time.deltaTime);
              }
              //morph to ramp//
              if(shapeN == )
              {
                     vertLeftTopFront = Vector3.Lerp(vertLeftTopFront, new Vector3(-,-,),Time.deltaTime);
                     vertRightTopFront = Vector3.Lerp(vertRightTopFront, new Vector3(,-,),Time.deltaTime);
                     vertRightTopBack = Vector3.Lerp(vertRightTopBack, new Vector3(,0.5f,-),Time.deltaTime);
                     vertLeftTopBack = Vector3.Lerp(vertLeftTopBack, new Vector3(-,0.5f,-),Time.deltaTime);
              }
              //morph to roof//
              if(shapeN == )
              {
                     vertLeftTopFront = Vector3.Lerp(vertLeftTopFront, new Vector3(-,0.2f,),Time.deltaTime);
                     vertRightTopFront = Vector3.Lerp(vertRightTopFront, new Vector3(,0.2f,),Time.deltaTime);
                     vertRightTopBack = Vector3.Lerp(vertRightTopBack, new Vector3(,0.2f,),Time.deltaTime);
                     vertLeftTopBack = Vector3.Lerp(vertLeftTopBack, new Vector3(-,0.2f,),Time.deltaTime);
              }
              Start();
       }
}