4558: [JLoi2016]方

4558: [JLoi2016]方

https://lydsy.com/JudgeOnline/problem.php?id=4558

分析：

　　容斥原理+各种神奇的计数。

　　如果没有被删除了的点的话，直接计算就好了。

统计出所有的竖直放置的正方形，然后每个正方形里包含其边长个数正方形。

设外边的正方形边长为a，公式就是$(n - a + 1) \times (m - a + 1) * a$，所以可以O(n)求出。

考虑减不合法的正方形。那么分为包含一个“坏点”，2个，3个，4个。

234的时候都可以直接枚举两个点，然后就可以确定出其他的两个点了，（这里可以确定两个点后，把所有枚举到的都加上，最后除以计算了多少次。三个的可以分别枚举三条边的时候都算上，所以除以3；4个点枚举边和对角线都算上了，所以除以6）。1个的最难算。

我们把一个点面向的四个方向分开计算，因为这是一个一样的过程。

可以知道，如果确定了一个点，和一个正方形（这个点在正方形的边上），那么就会确定唯一的一个以这个点为顶点的正方形

那么我们只需要计算有多少个正方形的边上有这个点就行了，

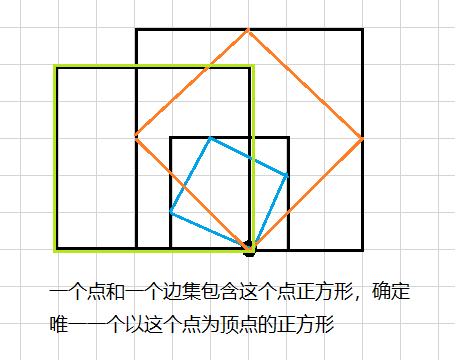
如果没有左边和右边的限制的话：

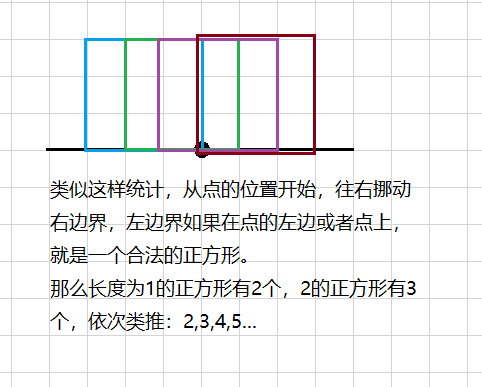
如上图，左边和右边长度都为4，先不管是否超出边界，那么就是2,3,4...8,9，分别表示长度为1,2,3...7,8的正方形。就是$\frac{n \times (n+3)}{2}$。

加上边界h的限制，正方形的边长最大为h。加上左右边界的限制，正方形的最大边长为$min(l+r,h)$，设为$z$。

这样算出来，可能是有不合法的，左边界超出了，或者右边界超出了。

于是根据等差序列求和公式，可以直接算了。

还有一点，计算这些正方形的时候，超四个方向的和加起来，会重复计算一部分。

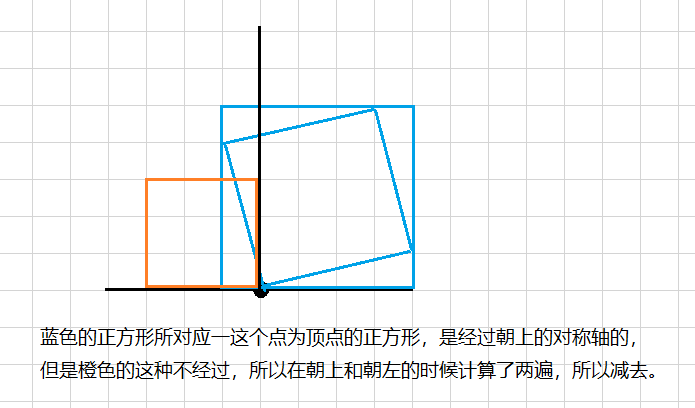
最后根据容斥原理，算出来就行了。

代码：

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<iostream>
 #include<cmath>
 #include<cctype>
 #include<set>
 #include<queue>
 #include<vector>
 #include<map>
 using namespace std;
 typedef long long LL;

 inline int read() {
     int x=,f=;char ch=getchar();for(;!isdigit(ch);ch=getchar())if(ch=='-')f=-;
     for(;isdigit(ch);ch=getchar())x=x*+ch-'';return x*f;
 }

 const int N = ;
 const int mod = 1e8 + ;

 struct Point{
     int x, y;
     Point() {}
     Point(int _x,int _y) { x = _x, y = _y; }
 }A[N];
 int n, m;
 LL ans, t1, t2, t3, t4;
 set<LL> s;

 LL Count1(int l,int r,int h) {
     int z = min(l + r, h);
     if (z == ) return ;
     LL ans = 1ll * z * (z + ) / ;
     if (z > l) ans -= 1ll * (z - l) * (z - l + ) / ;
     if (z > r) ans -= 1ll * (z - r) * (z - r + ) / ;
     return (ans + mod) % mod;
 }
 LL Calc1(int x,int y) { // 统计一个点可以作为多少个正方形的顶点。
     int u = x, d = n - x, l = y, r = m - y;
     LL ans = Count1(l, r, u) + Count1(l, r, d) + Count1(u, d, l) + Count1(u, d, r); ans %= mod;
     ans = ans - min(u, l) - min(u, r) - min(d, l) - min(d, r);
     return (ans + mod) % mod;
 }
 bool inmap(Point P) {
     return (P.x >=  && P.x <= n && P.y >=  && P.y <= m);
 }
 void Calc234(Point P,Point Q) {
     if (!inmap(P) || !inmap(Q)) return ;
     int t = s.count(1ll * P.x * (m + ) + P.y) + s.count(1ll * Q.x * (m + ) + Q.y);
     ++ t2;
     if (t >= ) t3 ++;
     if (t >= ) t3 ++, t4 ++;
 }
 int main() {
     n = read(), m = read();int k = read();
     for (int i = ; i <= k; ++i) {
         A[i].x = read(), A[i].y = read();
         s.insert(1ll * A[i].x * (m + ) + A[i].y); // 因为列是从0开始编号的，所以需要乘以(m+1)，或者直接乘以2000000
     }
     for (int i = , lim = min(n, m); i <= lim; ++i) {
         ans += (1ll * (n - i + ) * (m - i + ) % mod * i % mod);
         if (ans >= mod) ans -= mod;
     }
     for (int i = ; i <= k; ++i) {
         t1 += Calc1(A[i].x, A[i].y);
         if (t1 >= mod ) t1 -= mod;
     }
     for (int i = ; i <= k; ++i) {
         Point P = A[i];
         for (int j = i + ; j <= k; ++j) {
             Point Q = A[j];
             int dx = A[i].x - A[j].x, dy = A[i].y - A[j].y;
             Calc234(Point(P.x + dy, P.y - dx), Point(Q.x + dy, Q.y - dx)); // 作为边的情况
             Calc234(Point(P.x - dy, P.y + dx), Point(Q.x - dy, Q.y + dx));
             if ((abs(dx) + abs(dy)) & ) continue;
             int dx2 = (dx - dy) / , dy2 = (dx + dy) / ;
             Calc234(Point(P.x - dx2, P.y - dy2), Point(Q.x + dx2, Q.y + dy2)); // 作为对角线的情况
         }
     }
     ans = ans - t1 + t2 - t3 /  + t4 / ;
     ans = (ans + mod) % mod;
     cout << ans;
     return ;
 }