机器学习 之k-means和DBSCAN的区别

目录

• 1、定义和区别（优缺点对比）
• 2、kmeans原理
• 3、DBSCAN原理

1、定义和区别（优缺点对比）

• 聚类分为：基于划分、层次、密度、图形和模型五大类；

• 均值聚类k-means是基于划分的聚类， DBSCAN是基于密度的聚类。区别为：

  1. k-means需要指定聚类簇数k，并且且初始聚类中心对聚类影响很大。k-means把任何点都归到了某一个类，对异常点比较敏感。DBSCAN能剔除噪声，需要指定邻域距离阈值eps和样本个数阈值MinPts，可以自动确定簇个数。

  2. K均值和DBSCAN都是将每个对象指派到单个簇的划分聚类算法，但是K均值一般聚类所有对象，而DBSCAN丢弃被它识别为噪声的对象。

  3. K均值很难处理非球形的簇和不同大小的簇。DBSCAN可以处理不同大小或形状的簇，并且不太受噪声和离群点的影响。当簇具有很不相同的密度时，两种算法的性能都很差。

  4. K均值只能用于具有明确定义的质心（比如均值或中位数）的数据。DBSCAN要求密度定义（基于传统的欧几里得密度概念）对于数据是有意义的。

  5. K均值算法的时间复杂度是O(m)，而DBSCAN的时间复杂度是O(m^2)。

  6. DBSCAN多次运行产生相同的结果，而K均值通常使用随机初始化质心，不会产生相同的结果。

  7. K均值DBSCAN和都寻找使用所有属性的簇，即它们都不寻找可能只涉及某个属性子集的簇。

  8. K均值可以发现不是明显分离的簇，即便簇有重叠也可以发现，但是DBSCAN会合并有重叠的簇。

  9. K均值可以用于稀疏的高维数据，如文档数据。DBSCAN通常在这类数据上的性能很差，因为对于高维数据，传统的欧几里得密度定义不能很好处理它们。

2、kmeans原理

• k-means：即均值聚类，对于给定样本集，按照样本之间的距离大小，将样本集划分为K个簇。目标是让簇内的点尽量连接在一起，而让簇间的距离尽量大。
• 目标函数：如果用数据表达式表示，假设簇划分为(C1,C2,...Ck)，则我们的目标是最小化平方误差E：

\[E = \sum_{i=1}^{k} \sum_{x \in C_{i}} ||x- \mu_{i}||_{2}^{2}\]

其中\(\mu\)是簇\(C_{i}\)的均值向量，也称为质心，表达式为：

\[\mu_{i} = \frac{1}{C_{i}} \sum_{x \in C_{i}} x\]

• 直接求目标函数E的值是一个NP难的问题。NP(non-deterministic polynomial)是指非确定性多项式，即可用一定数量的运算去解决多项式时间内可解决的问题，而NP难不是一个NP问题。（NP->NPC->NP hard）

• K-means算法流程：首先确定K值（可以根据经验指定，或者交叉验证选择合适k值），其次是选择k个初始化的质心（质心的选择对结果的影响很大，因此质心选择不能太近）。
  

优化算法暂时不作笔记。

• k-means优点：

  1. 原理比较简单，实现也是很容易，收敛速度快。

  2. 聚类效果较优。

  3. 算法的可解释度比较强。

  4. 主要需要调参的参数仅仅是簇数k。

• k-means缺点：

  1. K值的选取不好把握。

  2. 对于不是凸的数据集比较难收敛。

  3. 如果各隐含类别的数据不平衡，比如各隐含类别的数据量严重失衡，或者各隐含类别的方差不同，则聚类效果不佳。

  4. 采用迭代方法，得到的结果只是局部最优。

  5. 对噪音和异常点比较的敏感。

3、DBSCAN原理

• DBSCAN定义：是一种基于密度的聚类算法，可以通过样本分布的紧密程度决定，同一类别的样本之间是紧密相连的，不同样本是是分离的。

• DBSCAN原理：基于一组邻域来描述样本集的紧密程度，参数\((\epsilon, MinPts)\)用来描述领域的样本分布紧密程度。其中\(\epsilon\)是某一样本的邻域距离阈值，\(MinPts\)描述了某一样本的距离为\(\epsilon\)的邻域中样本个数阈值。

• DBSCAN思想：由密度可达关系导出的最大密度相连的样本集合，即为我们最终聚类的一个类别，或者说一个簇。假定样本集为\(D=(x_{1},x_{2},...,x_{m})\)，则有以下重要定义：

  1. \(\epsilon\)-邻域：对于xj∈D，其ϵ-邻域包含样本集D中与xj的距离不大于ϵ的子样本集，即Nϵ(xj)={xi∈D|distance(xi,xj)≤ϵ}, 这个子样本集的个数记为|Nϵ(xj)|　；

  2. 核心对象：对于任一样本xj∈D，如果其ϵ-邻域对应的Nϵ(xj)至少包含MinPts个样本，即如果|Nϵ(xj)|≥MinPts，则xj是核心对象。　

  3. 密度直达：如果xi位于xj的ϵ-邻域中，且xj是核心对象，则称xi由xj密度直达。注意反之不一定成立，即此时不能说xj由xi密度直达, 除非且xi也是核心对象。

  4. 密度可达：对于xi和xj,如果存在样本样本序列p1,p2,...,pT,满足p1=xi,pT=xj, 且pt+1由pt密度直达，则称xj由xi密度可达。也就是说，密度可达满足传递性。此时序列中的传递样本p1,p2,...,pT−1均为核心对象，因为只有核心对象才能使其他样本密度直达。注意密度可达也不满足对称性，这个可以由密度直达的不对称性得出。

  5. 密度相连：对于xi和xj,如果存在核心对象样本xk，使xi和xj均由xk密度可达，则称xi和xj密度相连。注意密度相连关系是满足对称性的。

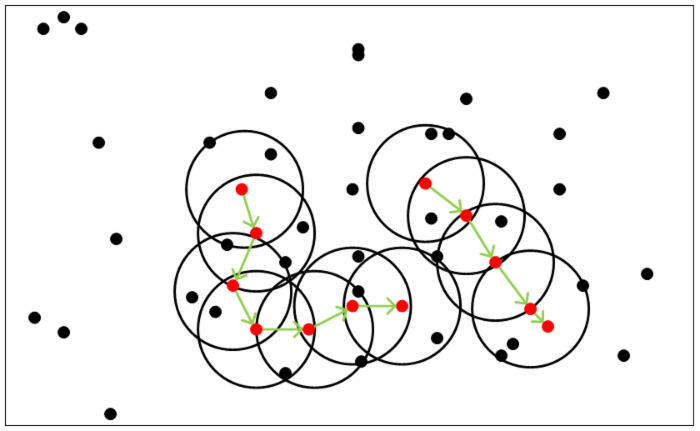
• DBSCAN聚类算法流程：
  

• DBSCAN优点：

  1. 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

  2. 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

  3. 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

• DBSSCAN缺点：

  1. 如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

  2. 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。

  3. 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。

• 凸集：集合中的任意两点连线的点都在该集合中，则称该集合为凸集；凹集为非凸集。而凸数据集是指集合以数据记录为点的集合。例如，\(ConvexSet = \{(x1,x2,...), (x1,x2,...)', (x1,x2,...)'',...,(x1,x2,...)^{n}\}\)

参考

1.[博客园]https://www.cnblogs.com/hdu-2010/p/4621258.html

2.[刘建平博客]https://www.cnblogs.com/pinard/p/6208966.html

3.[刘建平博客]https://www.cnblogs.com/pinard/p/6164214.html