强化学习4-时序差分TD

之前讲到强化学习在不基于模型时可以用蒙特卡罗方法求解，但是蒙特卡罗方法需要在每次采样时生产完整序列，而在现实中，我们很可能无法生成完整序列，那么又该如何解决这类强化学习问题呢？

由贝尔曼方程 v_π(s)=E_π(R_t+1+γR_t+2+γ²R_t+3+...|S_t=s) 推导可得 v_π(s)=E_π(R_t+1+γv_π(s_t+1)|s_t=s)，由此给我们的启发是，可以拿下一个状态的价值函数来表示当前状态的价值函数，即t+1时刻表示t时刻，这就引入了时序差分。

这样只需要两个连续的状态，就可以尝试解决强化问题了。

同蒙特卡罗一样，时序差分也可以解决预测和控制问题

从表现形式上对比分析TD与MC

1.时序差分不需要完整的状态序列

　　// 也就是说，时序差分可以在知道结果之前学习，或者说在没有结果时学习，还可以在持续进行的环境中学习 ；

　　// 而蒙特卡罗只能在知道结果时学习

2.蒙特卡罗是在真实的实验中用少数几次的值来近似真实值，而时序差分并没有真实的实验，而是完全瞎猜，即用随机数来初始化V (当然你也可以通过试验初始化)

3.正常情况下，蒙特卡罗的更新方式是 V(S_t)=V(S_t)+1/N(S_t) (G_t−V(S_t))，而时序差分没有N（状态s在完整序列中出现的次数），估只能用V(S_t)=V(S_t)+α (G_t−V(S_t)) 来更新

　　// 此处 G_t=R_t+1+γv_π(s_t+1)，称为S_t状态的TD目标值，v_π(s_t)是估计值，G_t-v_π(s_t)叫误差，α就是学习率，这里类似梯度下降。

4.蒙特卡罗使用实际的收获来更新状态价值，是某一策略下状态价值的无偏估计；

而时序差分使用TD目标值，即基于即时奖励和下一状态的估计值来替代当前状态的收获，属于状态价值的有偏估计

　　// 常用 v_π(s_t) 表示当前状态的实际价值

　　// 常用V_π(S_t) 表示当前状态的预估价值

　　// 一般为书写方便，随便写了

通常来讲，时序差分更加灵活，在主流的强化学习解决方法中，都是基于时序差分。

接下来我们看看时序差分解决预测问题

1.输入{S A R  π γ}

2.生成两个连续状态

　　// 由于时序差分用下一个状态更新当前状态，故首先要有2个状态，或者先初始化一个状态，此时再取下一个状态

3.计算TD目标值，并更新当前状态价值

4.取下一个状态，直至终点

5.重新从起点开始迭代

　　// 当然第五步中不一定必须从起点开始迭代，可以随机取状态

　　// 第四步中也不一定要取下一个状态，也可以随机取状态　　（后续会讲到q learning 和 sarsa时用到此点）

　　// 具体可以参考实际情况

6.直至收敛

实例对比TD和MC求解预测问题的不同

假设我们的强化学习问题有A,B两个状态，模型未知，不涉及策略和行为。只涉及状态转化和即时奖励。衰减因子为1。一共有8个完整的状态序列如下：

① A,0,B,0 ②B,1 ③B,1 ④ B,1 ⑤ B,1 ⑥B,1 ⑦B,1 ⑧B,0

1.对于MC

大体思路：MC是每次生成完整序列，然后计算该序列中每个状态的价值，最后根据完整序列个数进行累积均值更新。

换个更简单的说法，每个完整序列中该状态的价值，求和，再求平均

状态价值采用 G_t=R_t+1+γR_t+2+γ²R_t+3+...γ^_T−t−1R_T

那么上例中 A 只存在于1个完整序列中，估v=0/1=0，B存在于8个序列，故v=（0+1+1+..+0）/8=6/8

2.对于TD

大体思路：找到当前状态的下一个状态，然后用下一个状态的预估值和即时奖励来更新该状态的价值，再取状态

换个更简单的说法，用下一个状态来更新当前状态，之后再取一个状态，迭代，求平均

状态价值采用 v_π(s)=R_t+1+γv_π(s_t+1)

由于B没有后续状态，故v=所有回报/总个数=6/8，v(A)=R+γv(B)=6/8

N步时序差分

上面讲到用后一个状态来表示当前状态，那么能不能用后两个状态来表示呢？后三个呢？N个呢？都是可以的

相应TD目标值是

后一个 G_t⁽¹⁾=R_t+1+γv_π(S_t+1)　　　　　　　　　　　　　　　　　　　　　　　　TD(0)

后两个 G_t⁽²⁾=R_t+1+γR_t+2+γ²v_π(S_t+2)　　　　　　　　　　　　　　　　　　　　  TD(1)

后三个 G_t⁽³⁾=R+γR+γR_t+1t+2²_t+3+γv(S³_πt+3)

后N个  G_t⁽ⁿ⁾=R_t+1+γR_t+2+γ²R_t+3+...+γ^_n-1R_t+n+γ^_nV(S_t+n)

...

后∞个  G_t^{(∞)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　MC}

常定义为n-步收获（n-step return）

1. N步学习的价值更新公式

V(S_t)=V(S_t)+α(G_t^(n)-V(S_t))

2. N步学习 策略评估 步骤

首先，牢记这个公式  G_t⁽ⁿ⁾=R_t+1+γR_t+2+γ²R_t+3+...+γ^_n-1R_t+n+γ^_nV(S_t+n)

　　// t=0时，G_t⁽ⁿ⁾=R₁+γR₂+γ²R₃+...+γ^_n-1R_n+γ^_nV(S_n)

　　// n步，其实是从0走到n-1，就能得到R_n和V(S_n)

　　// 习惯上我们把 n步链条认为从0到n，只是方便理解

输入：{S A R π γ α}  n为步数，T为回合终点，初始化状态价值表

输出：状态价值表

1. 循环　　生成片段（从某点开始，到终点，一般从起点开始）

2. 对于片段中的每一步 t=0,1,2...n-1,n...T　　　

　　. 初始状态S根据π选择A，得到R和S'

　　. τ=t+1-n　　

　　　　// 这步首先是计数，看看t走到哪里了，够不够n步

　　　　// 如果t=0，n=1,0+1-1=0，状态比步数少1，所以+1，当前时刻的下一步就够n步

　　　　// 刚开始肯定是负数

　　. 当τ>=0　　（当t=n-1时，τ=0，从这一刻起，每个状态都可以往前推n步了，而此时需要从R₁开始算，而τ+1=1）

　　　　.. 计算GR，GR=Σ_i=τ+1 ^{min(τ+n, T)}γ^i-τ-1R_i（这就是TD目标值的全部R）　　　　

　　　　.. 如果τ+n<T，G=GR+γⁿV(S_τ+n)　　（这就是TD目标值，如果τ+n >T，说明片段已超过终点，不存在这种情况）

　　　　.. V(Sτ)=V(Sτ)+α(G-V(Sτ))　　

　　　　.. 直至终点　　　　　　　　　　　  （实际上只需到终点即可，无需判断τ+n<T，因为在终点之前，都是τ+n<T）

3. 直至v收敛

那么到底n取多少合适呢？

貌似并没有什么好的办法来确定，即使这个问题确定了，另外的问题不一定适用，所以索性取1到∞，于是引入了TD(λ)。

TD(λ)　λ€[0, 1]

这种方法其实是综合考虑了所有N步收获，但是如何综合？一般情况下是加权平均。

引入参数λ

1. λ 收获

　　// λ 收获 G_t^λ 综合考虑了1到∞的所有步收获，给每一步收获一个权重 (1-λ)λ^n-1  这样 G_t^λ=(1-λ)Σ₁^∞λ^(n-1)G_t⁽ⁿ⁾

2. λ 预测

　　// V_π(S_t)=V_π(S_t)+α(G_t⁽ⁿ⁾-V_π(S_t)　　

　　// 各步收获的权重分配图，图中最后一列 λ 的指数是 T-t-1。T 为终止状态的时刻步数，t为当前状态的时刻步数，所有的权重加起来为1。（最后一列的权重不是按上述权重公式计算，而是需要权重和为1，即1-前面的权重和）

　　

　　当λ为0时，退化为TD(0), 只有第一列

　　当λ为1时，退化为MC，只有最后一列

3. TD(λ)对于权重分配的图解

　　

　　// 例如对于 n=3 的3-步收获，赋予其在 λ 收获中的权重如左侧阴影部分面积，对于终止状态的T-步收获，T以后的所有阴影部分面积。而所有节段面积之和为1。这种几何级数的设计也考虑了算法实现的计算方便性。

　　TD(λ)的设计使得每个回合中，当前状态的的状态价值与后续所有状态的价值有关，也就是说当前状态的价值影响了之前所有状态的价值。只是影响的权重不同，距离越远，权重越小。

前向认识TD(λ)

注意这里的前向的方向是从当前状态到后续状态

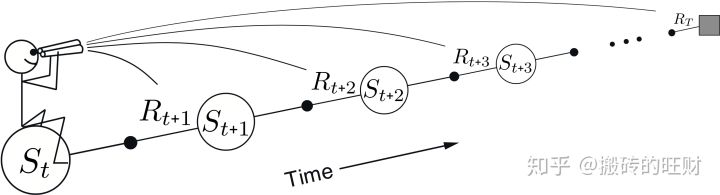
当我们拿着望远镜从当前状态向后续状态看，发现需要每个状态的价值，也就是需要走完整个回合，这和MC一样，需要完整序列，所以TD(λ)具有和MC一样的劣势。

后向认识TD(λ)

先看个例子，并引入一些概念

示例解释TD(λ) -- 被电击的原因

当老鼠听到3次响铃和看到1次亮灯后，被电击

那么老鼠被电击是因为响铃呢还是因为亮灯？还是两者兼有？兼有的话哪个更重要呢？

首先引入两个概念

1. 频率启发：将原因归结于发生频率最高的状态

2. 就近启发：将原因归结于最近发生的状态

再次引入一个概念

给每个状态设置一个资格迹（Eligibility Traces，ES，也叫效用迹，或效用追踪，后续会详细介绍），就是综合考虑 频率启发 和 就近启发

资格迹对应每个状态（或者s a）

E₀(s)=0　　　　　　每个s的初始值为0

E_t(s)=γλE_t-1(s)　　　t时刻的ES是前一时刻ES的衰减，如果该时刻没有发生s，如第3次响铃后下一个时刻是亮灯，没有发生响铃，那么这次响铃的ES就是衰减值

E_t(s)=γλE_t-1(s)+1　　t时刻的ES是前一时刻ES的衰减+1，如果该时刻发生了s，如第1次响铃后下一时刻是响铃，那么第1次响铃的ES就是衰减值+1

用图像来表示上面公式，一个可能的曲线图（该方法很多变种）

横坐标是时间，横坐标下的竖线代表发生了s状态；纵坐标是ES的值。

从图中可以看出，当某状态连续出现时，该状态的ES会在一定衰减的基础上，有一个单位的提高，此时将增加该状态对最终收获的影响比重，

同时，如果该状态距离最终状态较远，则其对最终收获的影响越小。

其实资格迹就是一个信度分配的问题。

比如我们下棋，最后输了，到底中间哪一步负责? 或者每一步都有责任，那么每一步的责任分别是多少呢？这就是一个信度分配的问题。

再如老鼠被电击，是因为响铃还是亮灯，合理的解释是两者都有，于是老鼠为这两个事件分别分配了权重，如果某个事件 s 发生，那么 s 对应的资格迹的值就加1，如果在某一段时间 s 未发生，则按照某个衰减因子进行衰减，这也就是上面的资格迹的计算公式了。

特别的， ES 值并不需要等到完整的episode结束才能计算出来，它可以每经过一个时刻就得到更新。 ES值存在饱和现象，有一个瞬时最高上限：E_max=1/(1-γλ) 

　　// ET是一个非常符合神经科学相关理论的、非常精巧的设计。把它看成是神经元的一个参数，它反映了神经元对某一刺激的敏感性和适应性。神经元在接受刺激时会有反馈，在持续刺激时反馈一般也比较强，当间歇一段时间不刺激时，神经元又逐渐趋于静

　　　息状态；同时不论如何增加刺激的频率，神经元有一个最大饱和反馈。）

案例结束 

重新认识后向视角

后向视角引入了资格迹的概念，每个状态都有一个资格迹。我们可以将资格迹理解为权重

　　// 离当前时刻越远，对价值函数的影响越小

　　// 被访问的次数越少，对价值函数影响越小

TD(λ)后向视角解释：有个人坐在状态流上，拿着话筒面向经历过的状态，并根据当前状态的回报和下一状态的价值函数得到TD偏差后，此人告诉经过的状态需要根据TD偏差更新自己的价值函数，更新的程度与经过的状态和当前状态的距离有关。

假设当前状态为 S_t，TD偏差为 δ_t，那么 S_t-1 处的值函数更新应该乘以一个衰减因子 γλ，状态S_t-2 处的值函数更新应该乘以 (γλ)²，以此类推。把刚才的描述体现在公式里更新状态价值，是这样的：

δ_t=R_t+1+γV(S_t+1)-V(S_t)

V(S)=V(S)+αδ_tE_t(S)

后向和前向可互推，结果一样，具体参考 https://zhuanlan.zhihu.com/p/51552679

时序差分解决控制问题

1.条件{S A R π γ} 探索率ε

2.状态动作价值

3.价值更新，选下一个状态动作

4.策略更新，可用 ε-贪心

总结

时序差分也是不基于模型的强化学习解决方法。

比蒙特卡罗更灵活，是目前主流强化学习的基本思想。