Spark MLlib 之 大规模数据集的相似度计算原理探索

无论是ICF基于物品的协同过滤、UCF基于用户的协同过滤、基于内容的推荐，最基本的环节都是计算相似度。如果样本特征维度很高或者<user, item, score>的维度很大，都会导致无法直接计算。设想一下100w*100w的二维矩阵，计算相似度怎么算？

更多内容参考——我的大数据学习之路——xingoo

在spark中RowMatrix提供了一种并行计算相似度的思路，下面就来看看其中的奥妙吧！

相似度

相似度有很多种，每一种适合的场景都不太一样。比如：

• 欧氏距离，在几何中最简单的计算方法
• 夹角余弦，通过方向计算相似度，通常在用户对商品评分、NLP等场景使用
• 杰卡德距离，在不考虑每一样的具体值时使用
• 皮尔森系数，与夹角余弦类似，但是可以去中心化。比如评分时，有人倾向于打高分，有人倾向于打低分，他们的最后效果在皮尔森中是一样的
• 曼哈顿距离，一般在路径规划、地图类中常用，比如A*算法中使用曼哈顿来作为每一步代价值的一部分（F=G+H, G是从当前点移动到下一个点的距离，H是距离目标点的距离，这个H就可以用曼哈顿距离表示）

在Spark中使用的是夹角余弦，为什么选这个，道理就在下面！

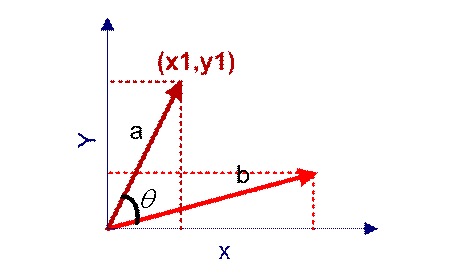
上面两个向量

\[\left( { x }_{ 1 },{ y }_{ 1 } \right)
\]

和

\[\left( { x }_{ 2 },{ y }_{ 2 } \right)
\]

计算其夹角的余弦值就是两个向量方向的相似度。

公式为：

\[cos(\theta )=\frac { a\cdot b }{ ||a||\ast ||b|| } \\ =\quad \frac { { x }_{ 1 }\ast { x }_{ 2 }\quad +\quad { y }_{ 1 }\ast y_{ 2 } }{ \sqrt { { x }_{ 1 }^{ 2 }+{ x }_{ 2 }^{ 2 } } \ast \sqrt { { y }_{ 1 }^{ 2 }+{ y }_{ 2 }^{ 2 } } }
\]

其中，\(||a||\)表示a的模，即每一项的平方和再开方。

公式拆解

那么如果向量不只是两维，而是n维呢？比如有两个向量：

\[第一个向量：({x}_{1}, {x}_{2}, {x}_{3}, ..., {x}_{n})\\
第二个向量：({y}_{1}, {y}_{2}, {y}_{3}, ..., {y}_{n})
\]

他们的相似度计算方法套用上面的公式为：

\[cos(\theta )\quad =\quad \frac { \sum _{ i=1 }^{ n }{ ({ x }_{ i }\ast { y }_{ i }) } }{ \sqrt { \sum _{ i=1 }^{ n }{ { x }_{ i }^{ 2 } } } \ast \sqrt { \sum _{ i=1 }^{ n }{ y_{ i }^{ 2 } } } } \\ =\quad \frac { { x }_{ 1 }\ast { y }_{ 1 }+{ x }_{ 2 }\ast { y }_{ 2 }+...+{ x }_{ n }\ast { y }_{ n } }{ \sqrt { \sum _{ i=1 }^{ n }{ { x }_{ i }^{ 2 } } } \ast \sqrt { \sum _{ i=1 }^{ n }{ y_{ i }^{ 2 } } } } \\ =\quad \frac { { x }_{ 1 }\ast { y }_{ 1 } }{ \sqrt { \sum _{ i=1 }^{ n }{ { x }_{ i }^{ 2 } } } \ast \sqrt { \sum _{ i=1 }^{ n }{ y_{ i }^{ 2 } } } } +\frac { { x }_{ 2 }\ast { y }_{ 2 } }{ \sqrt { \sum _{ i=1 }^{ n }{ { x }_{ i }^{ 2 } } } \ast \sqrt { \sum _{ i=1 }^{ n }{ y_{ i }^{ 2 } } } } +...+\frac { { x }_{ n }\ast { y }_{ n } }{ \sqrt { \sum _{ i=1 }^{ n }{ { x }_{ i }^{ 2 } } } \ast \sqrt { \sum _{ i=1 }^{ n }{ y_{ i }^{ 2 } } } } \\ =\quad \frac { { x }_{ 1 } }{ \sqrt { \sum _{ i=1 }^{ n }{ { x }_{ i }^{ 2 } } } } \ast \frac { { y }_{ 1 } }{ \sqrt { \sum _{ i=1 }^{ n }{ y_{ i }^{ 2 } } } } +\frac { { x }_{ 2 } }{ \sqrt { \sum _{ i=1 }^{ n }{ { x }_{ i }^{ 2 } } } } \ast \frac { { y }_{ 2 } }{ \sqrt { \sum _{ i=1 }^{ n }{ y_{ i }^{ 2 } } } } +...+\frac { { x }_{ n } }{ \sqrt { \sum _{ i=1 }^{ n }{ { x }_{ i }^{ 2 } } } } \ast \frac { { y }_{ n } }{ \sqrt { \sum _{ i=1 }^{ n }{ y_{ i }^{ 2 } } } }
\]

通过上面的公式就可以发现，夹角余弦可以拆解成每一项与另一项对应位置的乘积\({ x }_{ 1 }\ast { y }_{ 1 }\)，再除以每个向量自己的

\[\sqrt { \sum _{ i=1 }^{ n }{ { x }_{ i }^{ 2 } } }
\]

就可以了。

矩阵并行

画个图看看，首先创建下面的矩阵：



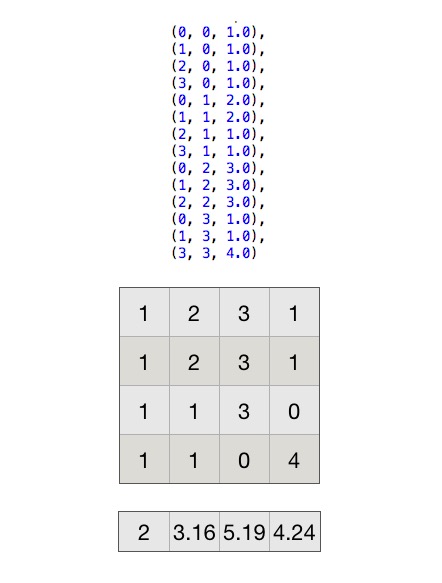
注意，矩阵里面都是一列代表一个向量....上面是创建矩阵时的三元组，如果在spark中想要创建matrix，可以这样：

val df = spark.createDataFrame(Seq(
      (0, 0, 1.0),
      (1, 0, 1.0),
      (2, 0, 1.0),
      (3, 0, 1.0),
      (0, 1, 2.0),
      (1, 1, 2.0),
      (2, 1, 1.0),
      (3, 1, 1.0),
      (0, 2, 3.0),
      (1, 2, 3.0),
      (2, 2, 3.0),
      (0, 3, 1.0),
      (1, 3, 1.0),
      (3, 3, 4.0)
    ))

    val matrix = new CoordinateMatrix(df.map(row => MatrixEntry(row.getAs[Integer](0).toLong, row.getAs[Integer](1).toLong, row.getAs[Double](2))).toJavaRDD)

然后计算每一个向量的normL2，即平方和开根号。



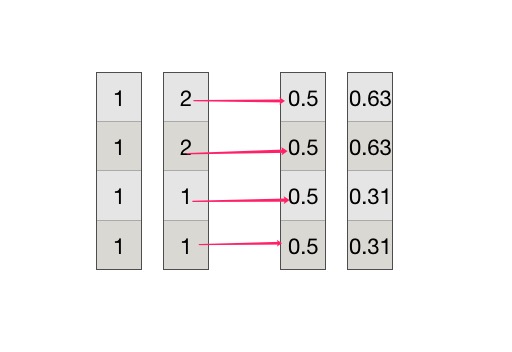
以第一个和第二个向量计算为例，第一个向量为(1,1,1,1)，第二个向量为(2,2,1,1)，每一项除以对应的normL2，得到后面的两个向量：

\[0.5*0.63+0.5*0.63+0.5*0.31+0.5*0.31 \approx 0.94
\]

两个向量最终的相似度为0.94。

那么在Spark如何快速并行处理呢？通过上面的例子，可以看到两个向量的相似度，需要把每一维度乘积后相加，但是一个向量一般都是跨RDD保存的，所以可以先计算所有向量的第一维，得出结果

\[(向量1的第1维，向量2的第1维，value)\\
(向量1的第2维，向量2的第2维，value)\\
...\\
(向量1的第n维，向量2的第n维，value)\\
(向量1的第1维，向量3的第1维，value)\\
..\\
(向量1的第n维，向量3的第n维，value)\\
\]

最后对做一次reduceByKey累加结果即可.....

阅读源码

首先创建dataframe形成matrix：

import org.apache.spark.mllib.linalg.distributed.{CoordinateMatrix, MatrixEntry}
import org.apache.spark.sql.SparkSession

object MatrixSimTest {
  def main(args: Array[String]): Unit = {
	// 创建dataframe，转换成matrix
    val spark = SparkSession.builder().master("local[*]").appName("sim").getOrCreate()
    spark.sparkContext.setLogLevel("WARN")

    import spark.implicits._

    val df = spark.createDataFrame(Seq(
      (0, 0, 1.0),
      (1, 0, 1.0),
      (2, 0, 1.0),
      (3, 0, 1.0),
      (0, 1, 2.0),
      (1, 1, 2.0),
      (2, 1, 1.0),
      (3, 1, 1.0),
      (0, 2, 3.0),
      (1, 2, 3.0),
      (2, 2, 3.0),
      (0, 3, 1.0),
      (1, 3, 1.0),
      (3, 3, 4.0)
    ))

    val matrix = new CoordinateMatrix(df.map(row => MatrixEntry(row.getAs[Integer](0).toLong, row.getAs[Integer](1).toLong, row.getAs[Double](2))).toJavaRDD)
    // 调用sim方法
    val x = matrix.toRowMatrix().columnSimilarities()
    // 得到相似度结果
    x.entries.collect().foreach(println)
  }
}

得到的结果为：

MatrixEntry(0,3,0.7071067811865476)
MatrixEntry(0,2,0.8660254037844386)
MatrixEntry(2,3,0.2721655269759087)
MatrixEntry(0,1,0.9486832980505139)
MatrixEntry(1,2,0.9128709291752768)
MatrixEntry(1,3,0.596284793999944)

直接进入columnSimilarities方法看看是怎么个流程吧！

def columnSimilarities(): CoordinateMatrix = {
  columnSimilarities(0.0)
}

内部调用了带阈值的相似度方法，这里的阈值是指相似度小于该值时，输出结果时，会自动过滤掉。

def columnSimilarities(threshold: Double): CoordinateMatrix = {
  //检查参数...

  val gamma = if (threshold < 1e-6) {
    Double.PositiveInfinity
  } else {
    10 * math.log(numCols()) / threshold
  }

 columnSimilaritiesDIMSUM(computeColumnSummaryStatistics().normL2.toArray, gamma)
}

这里的gamma用于采样，具体的做法咱们来继续看源码。然后看一下computeColumnSummaryStatistics().normL2.toArray这个方法：

def computeColumnSummaryStatistics(): MultivariateStatisticalSummary = {
  val summary = rows.treeAggregate(new MultivariateOnlineSummarizer)(
    (aggregator, data) => aggregator.add(data),
    (aggregator1, aggregator2) => aggregator1.merge(aggregator2))
  updateNumRows(summary.count)
  summary
}

之前有介绍这个treeAggregate是一种带“预reduce”的map-reduce，返回的summary，里面帮我们统计了每一个向量的很多指标，比如

currMean 	为 每一个向量的平均值
currM2 		为 每个向量的每一维的平方和
currL1 		为 每个向量的绝对值的和
currMax 	为 每个向量的最大值
currMin 	为 每个向量的最小值
nnz 		为 每个向量的非0个数

这里我们只需要currM2，它是每个向量的平方和。summary调用的normL2方法：

override def normL2: Vector = {
  require(totalWeightSum > 0, s"Nothing has been added to this summarizer.")

  val realMagnitude = Array.ofDim[Double](n)

  var i = 0
  val len = currM2.length
  while (i < len) {
    realMagnitude(i) = math.sqrt(currM2(i))
    i += 1
  }
  Vectors.dense(realMagnitude)
}

上面这步就是对平方和开个根号，这样就求出来了每个向量的分母部分。

下面就是最关键的地方了：

private[mllib] def columnSimilaritiesDIMSUM(
      colMags: Array[Double],
      gamma: Double): CoordinateMatrix = {
    // 一些参数校验

	// 对gamma进行开方
    val sg = math.sqrt(gamma) // sqrt(gamma) used many times

    // 这里把前面算的平方根的值设置一个默认值，因为如果为0，除0会报异常，所以设置为1
    val colMagsCorrected = colMags.map(x => if (x == 0) 1.0 else x)

	// 把抽样概率数组 和 平方根数组进行广播
    val sc = rows.context
    val pBV = sc.broadcast(colMagsCorrected.map(c => sg / c))
    val qBV = sc.broadcast(colMagsCorrected.map(c => math.min(sg, c)))

	// 遍历每一行，计算每个向量该维的乘积，形成三元组
    val sims = rows.mapPartitionsWithIndex { (indx, iter) =>
      val p = pBV.value
      val q = qBV.value
	  // 获得随机值
      val rand = new XORShiftRandom(indx)
      val scaled = new Array[Double](p.size)
      iter.flatMap { row =>
        row match {
          case SparseVector(size, indices, values) =>
	        // 如果是稀疏向量，遍历向量的每一维，除以平方根
            val nnz = indices.size
            var k = 0
            while (k < nnz) {
              scaled(k) = values(k) / q(indices(k))
              k += 1
            }

			// 遍历向量数组，计算每一个数值与其他数值的乘机。
			// 比如向量(1, 2, 0 ,1)
			// 得到的结果为 (0,1,value)(0,3,value)(2,3,value)
            Iterator.tabulate (nnz) { k =>
              val buf = new ListBuffer[((Int, Int), Double)]()
              val i = indices(k)
              val iVal = scaled(k)
              // 判断当前列是否符合采样范围，如果小于采样值，就忽略
              if (iVal != 0 && rand.nextDouble() < p(i)) {
                var l = k + 1
                while (l < nnz) {
                  val j = indices(l)
                  val jVal = scaled(l)
                  if (jVal != 0 && rand.nextDouble() < p(j)) {
	                // 计算每一维与其他维的值
                    buf += (((i, j), iVal * jVal))
                  }
                  l += 1
                }
              }
              buf
            }.flatten
          case DenseVector(values) =>
	        // 跟稀疏同理
            val n = values.size
            var i = 0
            while (i < n) {
              scaled(i) = values(i) / q(i)
              i += 1
            }
            Iterator.tabulate (n) { i =>
              val buf = new ListBuffer[((Int, Int), Double)]()
              val iVal = scaled(i)
              if (iVal != 0 && rand.nextDouble() < p(i)) {
                var j = i + 1
                while (j < n) {
                  val jVal = scaled(j)
                  if (jVal != 0 && rand.nextDouble() < p(j)) {
                    buf += (((i, j), iVal * jVal))
                  }
                  j += 1
                }
              }
              buf
            }.flatten
        }
      }
    // 最后再执行一个reduceBykey，累加所有的值，就是i和j的相似度
    }.reduceByKey(_ + _).map { case ((i, j), sim) =>
      MatrixEntry(i.toLong, j.toLong, sim)
    }
    new CoordinateMatrix(sims, numCols(), numCols())
  }

这样把所有向量的平方和广播后，每一行都可以在不同的节点并行处理了。

总结来说，Spark提供的这个计算相似度的方法有两点优势：

1. 通过拆解公式，使得每一行独立计算，加快速度
2. 提供采样方案，以采样方式抽样固定的特征维度计算相似度

不过杰卡德目前并不能使用这种方法来计算，因为杰卡德中间有一项需要对向量求dot，这种方式就不适合了；如果杰卡德想要快速计算，可以去参考LSH局部敏感哈希算法，这里就不详细说明了。