WHY数学表达式的3D可视化

很早之前我就有这种想法,将数学表达式的图形显示出来.最近终于实现了这套较为完善的版本,将其代码公布,也为开源做点贡献.首先系统中定义一套脚本语言格式,用于描述数学表达式.使用时先要将数学表达式写成该脚本的形式,解析脚本代码以生成相应的图形.该系统能够生成三维曲线图形和曲面图形.

开发环境:VS2008,图形渲染用的是D3D9,用于解析数学表达式的核心代码MathExpression只使用了C的基本库函数,可以跨平台使用.

软件下载地址:

http://files.cnblogs.com/WhyEngine/MathGraph_2_0.zip

代码下载地址:

http://pan.baidu.com/s/1pJkD4Bh

早期版本地址:

http://www.cnblogs.com/WhyEngine/p/3535903.html

补丁下载地址:

http://files.cnblogs.com/WhyEngine/MathExpression.zip修改了几个表达式解析错误的BUG,支持科学计数格式.

[一]软件介绍

(1)主界面

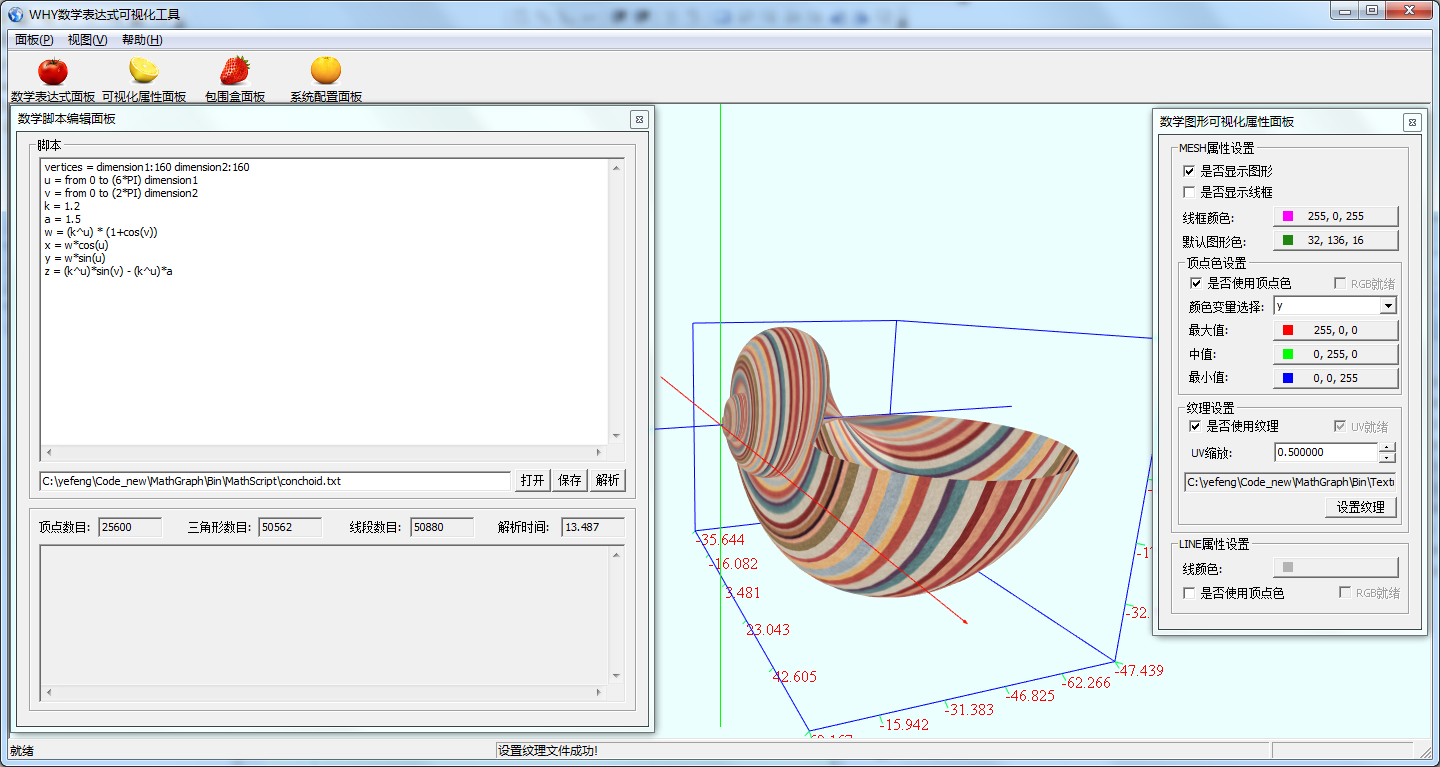
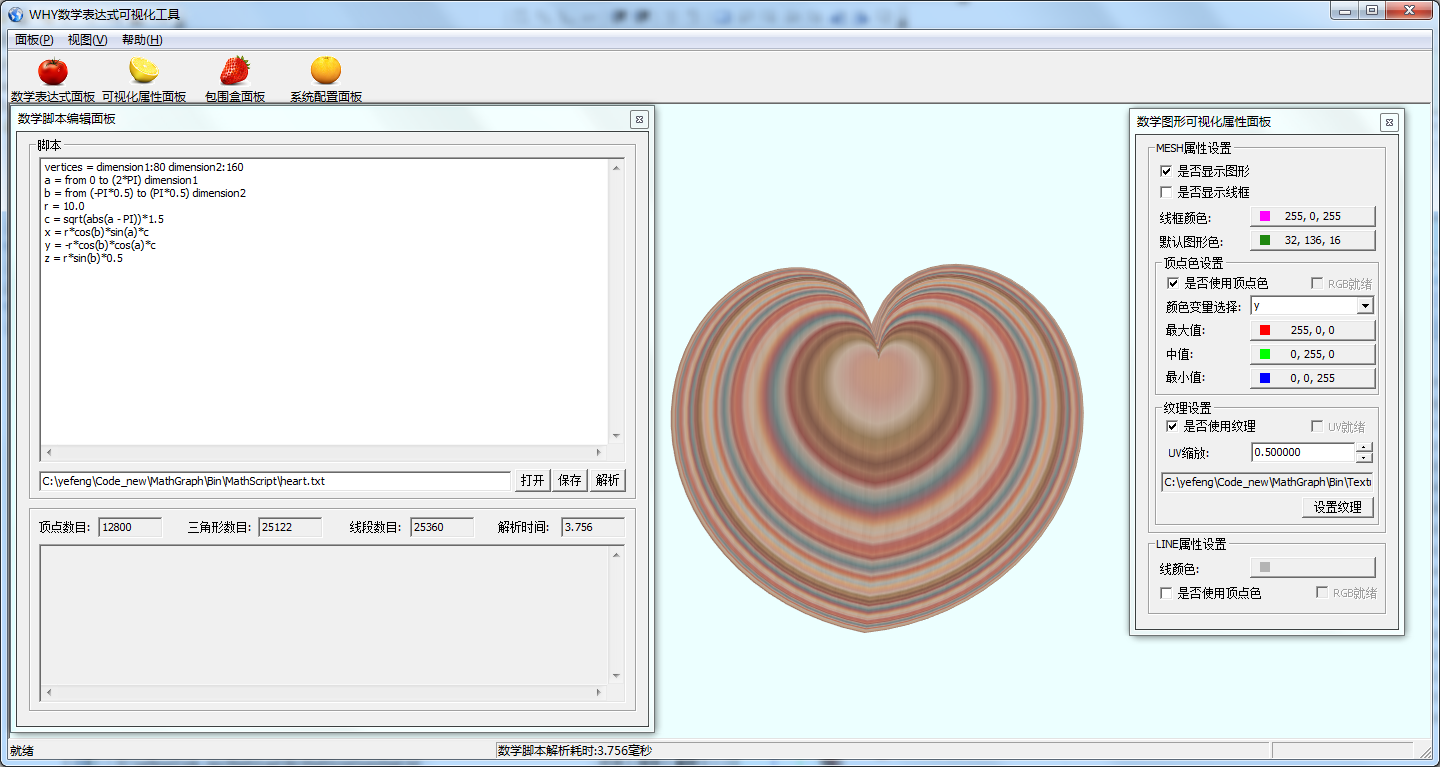
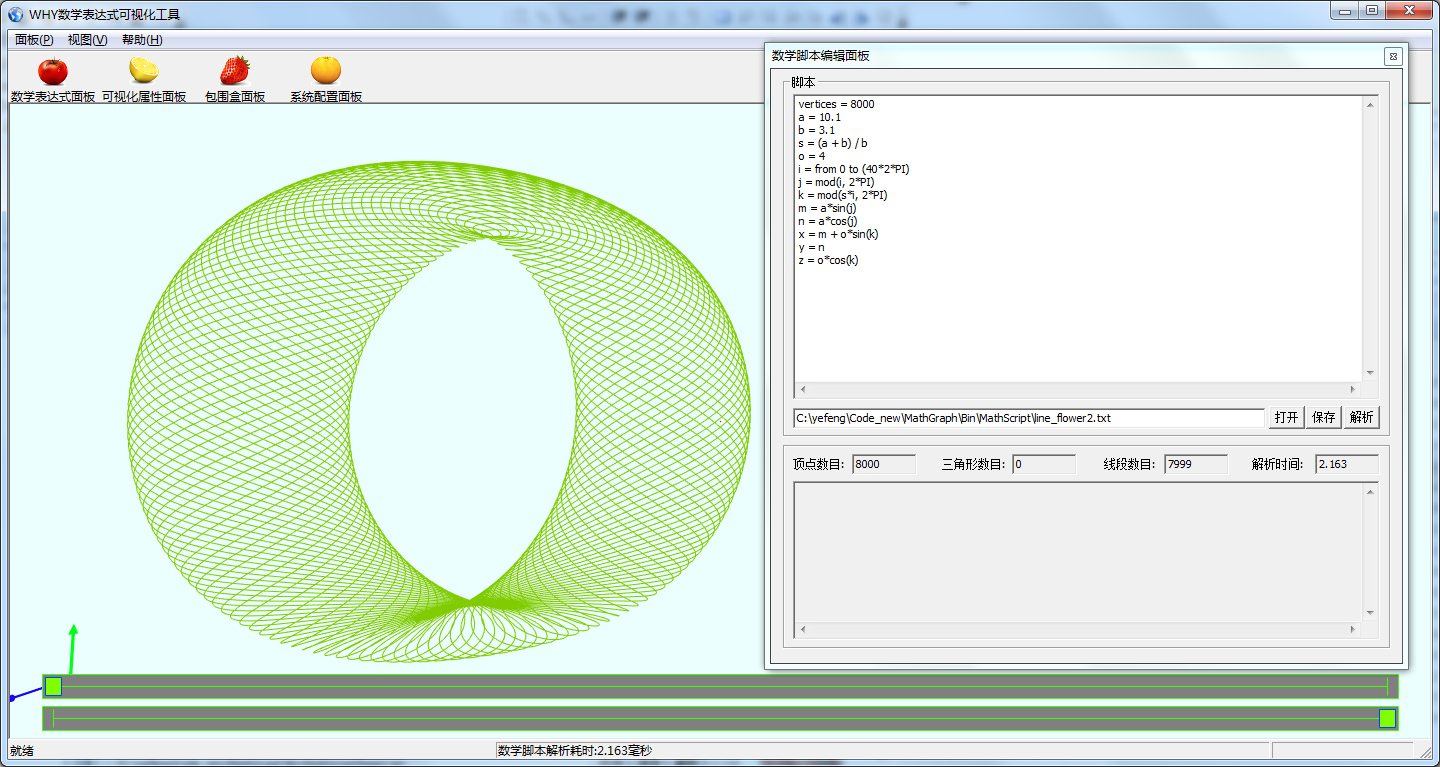
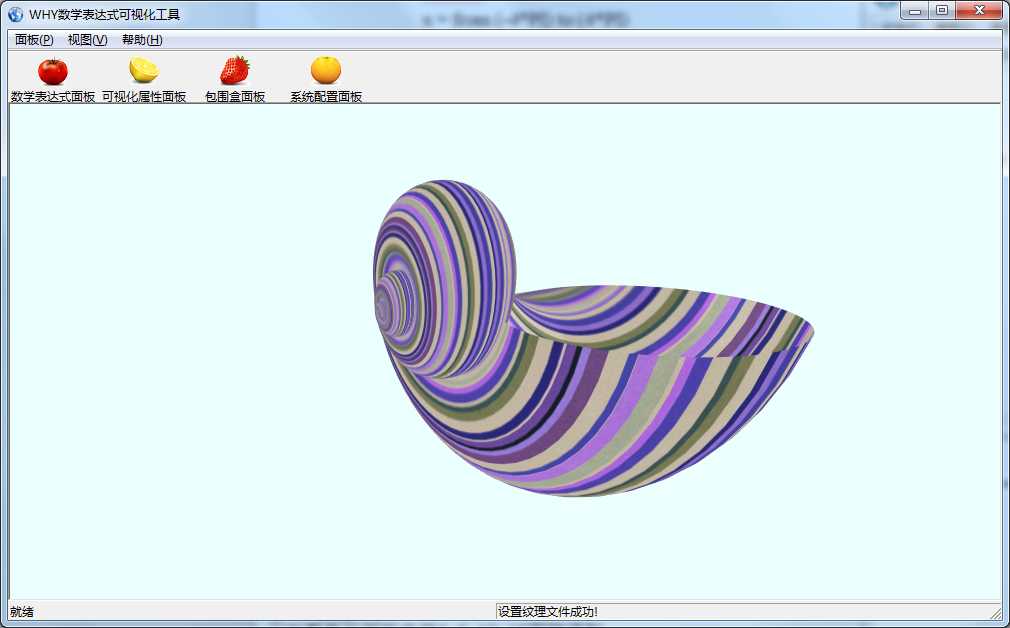
将数学脚本文件拖入到主界面中,可以显示其图形.亦可以通过菜单项打开脚本文件.

(2)数学脚本面板

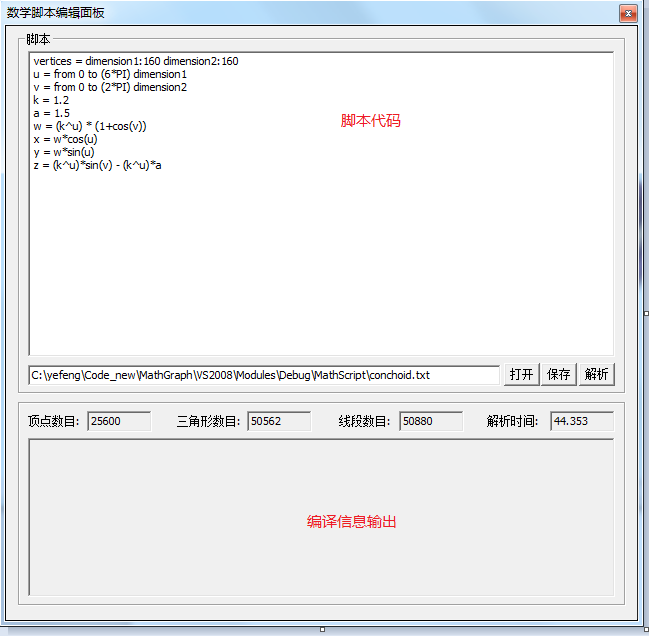
用于打开脚本文件,编辑脚本,保存文件,解析脚本,输出编译信息.

(3)可视化属性面板

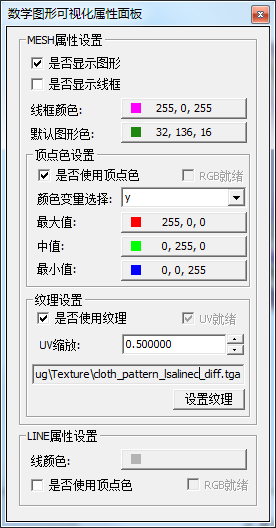
用于对图形显示的设置,如果设置颜色,纹理等.有两种类型的图形,MESH和曲线.将纹理文件拖入软件界面中后,会自动将其设置为MESH纹理.

(4)包围盒面板

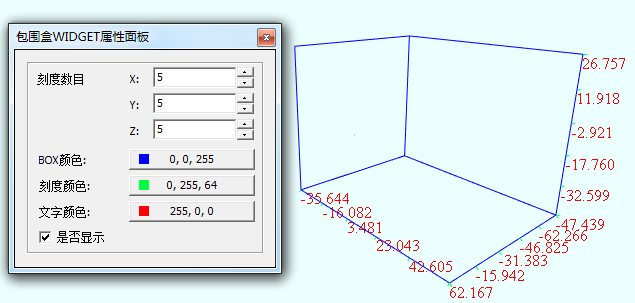
图形包围盒的显示.

(5)系统配置面板

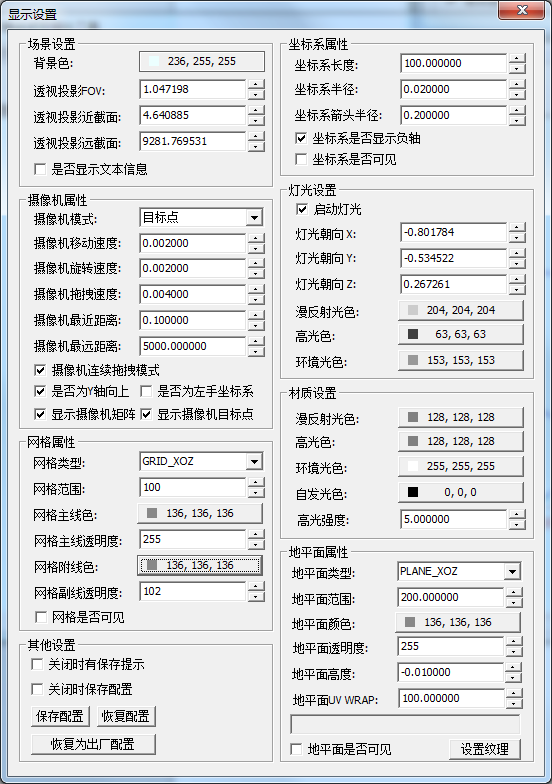
设置场景相关的属性,并能够保存配置文件.

(6)快捷方式

F5: 数学脚本编辑界面

F6: 可视化属性面板

F7: 包围盒面板

F9: 系统配置面板

F11: 全屏切换

ESC: 退出全屏

‘X’: 恢复为默认视角

'L': 开关灯光

'B': 包围盒的可见属性切换

'G': 地平面网格的可见属性切换

'M': 坐标系轴的可见属性切换

'N': 地面的可见属性切换

'1': MESH图形中,面片可见,线框不可见

'2': MESH图形中,面片不可见,线框可见

'3': MESH图形中,面片可见,线框可见

'4': MESH图形中,使用纹理色

'5': MESH图形中,使用顶点色

'6': MESH图形中,使用默认色

'0': 重新编译脚本(如果脚本中使用了随机数函数,则重新编译后,生成的图形会不一样)

[二]脚本语法

(1)常量

系统中默认有两个常量值

PI 3.1415927

E 2.7182818

常量名通常为大写字母,如 (PI + E) 或 sin(PI*0.5)

(2)数值解析

对整数的解析支持2,8,10,16四种进制

0X开头为16进制, XABCDEF大小写都可以, 如0xffff

0Y开头为2进制, Y大小写都可以, 如0y10101010000

0开头为8进制, 如07523, 注意出现了"08"之类的会解析失败

默认为10进制

对浮点数的解析只支持形如”0.12”的格式,不能省略前面的0,目前尚不支持科学表达.

(3)顶点数目

所谓顶点数目是指表达式运算时所需要的输入数据.数据分为两类:一维数据用于生成曲线图形,其定义如下:

vertices = 3600 // 设置顶点数目

二维数据用于生成生成MESH图形数据,其定义如下:

vertices = dimension1:80 dimension2:160 或

vertices = D1:80 D2:160

表示第一个维度的输入为80,第二个维度的输入为160,整体输入的顶点数目为80*160.

(4)变量及其赋值

系统中使用a-z的26个英文小写字母表示变量,变量能够存储单个实数,或一个实数数组.如果为实数数据,则其大小为之前设置的顶点数目(见3).

设置为单个实数

a = 3.1415 // 将a赋值为3.1415

一维数组的设置

a = from 0 to 100 // a为一个实数数组,数组大小为vertices的设置,数值为线性插值求得.

二维数据的设置

a = from 0 to (2*PI) dimension1

b = from (-PI*0.5) to (PI*0.5) dimension2

或者

a = from 0 to (2*PI) D1

b = from (-PI*0.5) to (PI*0.5) D2

变量中x,y,z将组成3D顶点位置坐标

r,g,b将组成顶点颜色.其值范围在0-1.0之间.如果没有设置r,g,b,将使用默认方式生成顶点色.

u,v为顶点的纹理坐标,如果没有设置u,v,将使用x,z生成顶点的纹理坐标.

(5)运算符

a.标准单目运算符

+,-

如:a = -b

b.标准双目运算符

+,-,*,/,%,^

如:c = a * b 如果a,b都为单个实数则运算结果c也是单个实数,否则c为实数数组

c.函数单目运算符形如sin(a)

positive,negative,abs,floor,ceil,sign,sqrt,exp,log,log2,log10,sin,cos,tan,asin,acos,atan,rand

d.函数双目运算符形如pow(a, b)

add,sub,multiply,divide,max,min,mod,pow,atan2,rand2,

e.函数三目运算符形如lerp(a, b, r)

lerp,clamp,gray,add3,min3,max3,average3

f.函数四目运算符形如average4(a, b, c, d)

add4,min4,max4,average4

g.函数数组运算符(输入实数数组,输出一个浮点数,如求最大值,最小值,数组加和等)

add_array,min_array,max_array,ave_array

h.函数数组运算符(输入实数数组,输出也是实数数组,如求数组左移,数组右移,前向累加等)

array_move_right,array_move_left,array_cumulate

(6)运算符嵌套

支持{}, [], ()这三类括号标志符,括号必需成对出现.支持最大32级括号的嵌套.如:

(2+(-2+(5.0*(9 + ((1+2)*3))/3) + 2))

-{exp[5*sqrt(1 -abs[sin{rand(100)}]) + 6]}

(7)示例

Sin曲线

vertices = 1200

x = from (-4*PI) to (4*PI)

y = sin(x)

圆

vertices = 360

w = from 0 to (2*PI)

r = 10.0

x = r*sin(w)

y = r*cos(w)

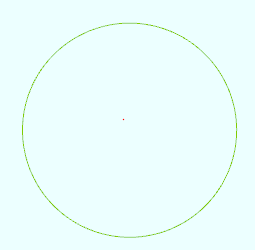
曲线球

vertices = 3600

w = from 0 to 32

a = mod(w, 1) * 2 * PI

b = from 0 to PI

r = 10.0

x = r*sin(a)*sin(b)

y = r*cos(a)*sin(b)

z = r*cos(b)

线圈

vertices = 36000

a = rand2(8, 64)

b = rand2(4, 64)

c = a + b

s = c / b

o = rand2(4, b)

i = from 0 to (360*2*PI)

j = mod(i, 2*PI)

k = mod(s*i, 2*PI)

m = a*sin(j)

n = a*cos(j)

x = m + o*sin(k)

y = n + o*cos(k)

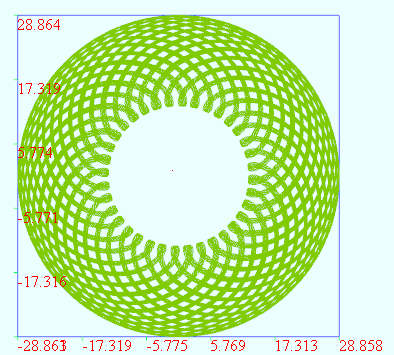
地形面

vertices = dimension1:320 dimension2:320

x = from (-4) to (4) dimension1

z = from (-4) to (4) dimension2

r = x^2 + z^2

y = sin(x^2 + z^2*3)/(0.05 + r) + (x^2 + z^2*5)*exp(1 -r)/2

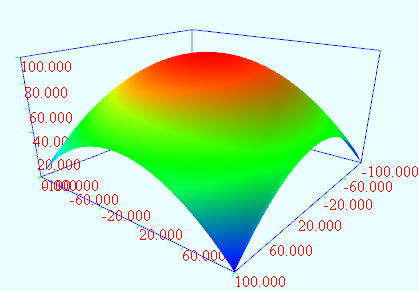
抛物线曲面

vertices = dimension1:101 dimension2:101

x = from (-100) to (100) dimension1

z = from (-100) to (100) dimension2

y = (20000 - x^2 - z^2)*0.005

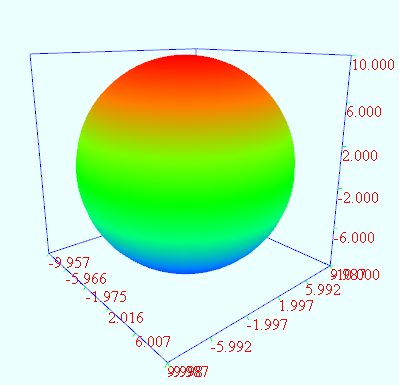
三维球体

vertices = dimension1:36 dimension2:72

a = from 0 to (2*PI) dimension1

b = from (-PI*0.5) to (PI*0.5) dimension2

r = 10.0

x = r*cos(b)*sin(a)

y = r*sin(b)

z = r*cos(b)*cos(a)

圆锥体

vertices = D1:72 D2:72

u = from 0 to (2) D2

v = from 0 to (2*PI) D1

a = 1.0

b = 0.5

c = sin(v);d = cos(v);

e = sin(b);f = cos(b);

g = sin(a);h = cos(a);

x = f*h*d - f*g*c + e*3

y = g*d + h*c

z = -e*h*d + e*g*c + f*3

x = x*u

y = y*u

z = z*u

心形

vertices = dimension1:80 dimension2:160

a = from 0 to (2*PI) dimension1

b = from (-PI*0.5) to (PI*0.5) dimension2

r = 10.0

c = sqrt(abs(a - PI))*1.5

x = r*cos(b)*sin(a)*c

y = -r*cos(b)*cos(a)*c

z = r*sin(b)*0.5

海螺

vertices = dimension1:160 dimension2:160

u = from 0 to (6*PI) dimension1

v = from 0 to (2*PI) dimension2

k = 1.2

a = 1.5

w = (k^u) * (1+cos(v))

x = w*cos(u)

y = w*sin(u)

z = (k^u)*sin(v) - (k^u)*a

环

vertices = D1:20 D2:500

u = from 0 to (2*PI) D1

v = from 0 to (2*PI) D2

a = sin(u)

b = cos(u)

c = sin(v)

d = cos(v)

r = (12 + c + b) *(1+d)

v = 10 * v

x = r*sin(v)

y = a + 32*d

z = r*cos(v)

[三]代码与用户自定义扩展

代码中MathExpression模块中为数学表达式及脚本解析的代码逻辑.

(1)主要接口

文件”math_expression_parser.h”提供了对表达式的解析函数

// 设置参数值

void SetParameterValue(char c, float value);

// 清空参数值

void ClearParameterValues();

// 表达式解析

bool ParseExpression(const char* szExpression, float& rst);

// 括号内的子表达式解析

bool ParseBracketExpression(const char* szExpression,

unsigned int& pos, float& rst,

unsigned int bracketIndex, bool endComma);

可以针求独立表达式的结果,如:

bool sus = ParseExpression(“sin(PI*3) + 10*E*log(100)”, rst);

文件”math_script_parser.h”提供了一个对象MathScriptParser,用于对数学脚本的解析

class MathScriptParser

{

public:

...

// 加载脚本文件

bool LoadFile(const char* szFile);

// 处理内存数据

bool ProcessMemory(const char* bufPtr, unsigned int bufSize);

...

};

(2)添加或设置常量值

开发者可以通过”const_value.h”文件中的如下函数对常量进行添加或修改

// 添加或设置常量值

bool SetConstValue(const char* szName, float value);

(3)添加或设置函数运算符

程序中的运算符操作是以函数指针的方式使用,开发者可以将自己实现的函数设置到系统中.

有6种运算符函数类型:

// 单目运算函数

typedef float (*SINGLE_OPERATOR_FUNC)(float);

// 双目运算函数

typedef float (*TWIN_OPERATOR_FUNC)(float, float);

// 三目运算函数

typedef float (*THREE_OPERATOR_FUNC)(float, float, float);

// 四目运算函数

typedef float (*FOUR_OPERATOR_FUNC)(float, float, float, float);

// 对ValueNode的运算函数(输入ValueNode,输出一个浮点数)

typedef float (*VALUENODE_TO_FLOAT_OPERATOR_FUNC)(const ValueNode*);

// 对ValueNode的运算函数(输入ValueNode,输出ValueNode)

typedef void (*VALUENODE_CONVERT_OPERATOR_FUNC)(const ValueNode*, ValueNode*);

开发者可自定义运算函数后,使用如下接口,将其添加到系统中.

// 添加或设置运算函数

bool SetSingleOperator(const char* szName, SINGLE_OPERATOR_FUNC func);

bool SetTwinOperator(const char* szName, TWIN_OPERATOR_FUNC func);

bool SetThreeOperator(const char* szName, THREE_OPERATOR_FUNC func);

bool SetFourOperator(const char* szName, FOUR_OPERATOR_FUNC func);

bool SetValueNodeToFloatOperator(const char* szName, VALUENODE_TO_FLOAT_OPERATOR_FUNC func);

bool SetValueNodeConvertOperator2(const char* szName, VALUENODE_CONVERT_OPERATOR_FUNC func);

需要注意这两个宏:

#define OPERATOR_NAME_LENGTH 24 // 操作符名的最大长度

#define MAX_FUNCTIONS_COUNT 256 // 运算函数的最大数目

如果不满足要求,请自己修改这两个宏值,不要出现内存越界.