机器学习：python使用BP神经网络示例

1.简介(只是简单介绍下理论内容帮助理解下面的代码，如果自己写代码实现此理论不够)

1） BP神经网络是一种多层网络算法，其核心是反向传播误差，即： 使用梯度下降法(或其他算法)，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。

BP神经网络模型拓扑结构包括输入层（input）、隐藏层(hidden layer)和输出层(output layer)，每层包含多个神经元。

2）BP神经网络示例图

上图就是一个简单的三层BP神经网络。网络共有6个单元，O₀用于表示阈值，O₁、O₂为输入层，O₃、O₄为第一隐层，也是唯一隐层，O₅为输出层单元。网络接收两个输入 ，发送一个输出 。每个单元接收一组输入，发送一个输出。 为权值,例如W₄₀ 表示O₀与O₄之间的权重。

3）神经单元(计算单元)

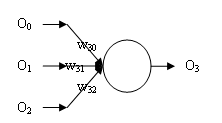
如上图所示，每个圆表示一个神经单元。其接收一组数据，经过计算输出一个数据。

4）传播过程

a）正向传递

例如：从O₁-->O₄-->0_5,这是正向传递过程中的一个路径(O₄除了接收O₁,还接收O₀、O₂的输入)。这里重点说下权重，W₄₁表示O₁和O₄之间的权重，假如O₁=1,O₄=4,W₄₁=0.5,那么O₅=1*4*0.5=2(2不是最终输出，最终输出还需要加上O₀、O₂ 的计算结果).

b）反向传递（过程比较复杂，这个表述不是特别精确，只是为了方便理解）

例如：从O₁<--O₄<--0_5,在这个过程中，O₅是计算出的值，参与计算的O₄的值不是其本身的值，而是在正向传递过程中计算出的值（即输出值）。而权重也是这个过程中调整的。

2.MLPClassifier函数

此函数是sklearn.neural_network中的函数，它是利用反向传播误差进行计算的多层感知器算法。

a) 主要参数

hidden_​​layer_sizes：隐藏层，例如:(5,2) 表示有2个隐藏层，第一隐藏层有5个神经单元，第二个隐藏层有2个神经单元；(5,2,4)表示有三个隐藏层。

activation：激活函数，在反向传递中需要用到。有以下四个可选项：

'identity':无激活操作，有助于实现线性瓶颈, 返回 f(x) = x

'logistic':逻辑函数, 返回 f(x) = 1 / (1 + exp(-x)).

'tanh': 双曲线函数, 返回 f(x) = tanh(x).

'relu': 矫正线性函数, 返回 f(x) = max(0, x)，（默认）

solver：反向传播过程中采用的算法，有以下三个选项：

'lbfgs': 准牛顿算法.适用于较小数据集

'sgd': 随机梯度下降算法.

'adam':优化的随机梯度下降算法(默认)。适用于较大数据集

alpha：L2惩罚系数

learning_rate：学习速率，有以下几个选项：(只有当slver='sgd'时有用)

constant:参数learning_rate_init指定的恒定学习速率.(默认选项)

invscaling’:使用“scale_t”的反向缩放指数逐渐降低每个时间步长t 的学习率。effective_learning_rate = learning_rate_init / pow（t，power_t）(power_t是另外一个参数)

adaptive: 自适应，只要损失不断下降就是用learning_rate_init。否则会自动调整(由另外一个参数tol决定)。

learning_rate_init:初始学习速率

b)属性

coefs_：权重列表

n_layers_：神经网络的总层数

3.示例一

本示例使用的数据：机器学习：从编程的角度去理解逻辑回归 。在下面的参数情况下正确率95%。

import numpy as np
import os
import pandas as pd
from sklearn.neural_network import MLPClassifier

def loadDataSet():
    ##运行脚本所在目录
    base_dir=os.getcwd()
    ##记得添加header=None，否则会把第一行当作头
    data=pd.read_table(base_dir+r"\lr.txt",header=None)
    ##dataLen行dataWid列 ：返回值是dataLen=100 dataWid=3
    dataLen,dataWid = data.shape
    ##训练数据集
    xList = []
    ##标签数据集
    lables = []
    ##读取数据
    for i in range(dataLen):
        row = data.values[i]
        xList.append(row[0:dataWid-1])
        lables.append(row[-1])
    return xList,lables

def GetResult():
    dataMat,labelMat=loadDataSet()
    clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
                        hidden_layer_sizes=(5,2), random_state=1)
    clf.fit(dataMat, labelMat)
    #print("层数----------------------")
    #print(clf.n_layers_)
    #print("权重----------------------")
    #for cf in clf.coefs_:
    #    print(cf)
    #print("预测值----------------------")
    y_pred=clf.predict(dataMat)
    m = len(y_pred)
    ##分错4个
    t = 0
    f = 0
    for i in range(m):
        if y_pred[i] ==labelMat[i]:
            t += 1
        else :
            f += 1
    print("正确:"+str(t))
    print("错误:"+str(f))

if __name__=='__main__':
    GetResult()

4.示例二(数据来源)

这次使用的数据还是红酒。因为红酒的口感得分是整数，所以也可以当作是分类。但是针对此实验数据，在多次调整参数的过程中（主要是调整隐藏层）正确率最高只有61%。这正是BP神经网络的一个缺陷:隐含层的选取缺乏理论的指导。

代码：

import numpy as np
import os
import pandas as pd
from sklearn.neural_network import MLPClassifier

##运行脚本所在目录
base_dir=os.getcwd()
##记得添加header=None，否则会把第一行当作头
data=pd.read_table(base_dir+r"\wine.txt",header=None,sep=';')
##dataLen行dataWid列 ：返回值是dataLen=1599 dataWid=12
dataLen,dataWid = data.shape

##训练数据集
xList = []
##标签数据集
lables = []
##读取数据
for i in range(dataLen):
    row = data.values[i]
    xList.append(row[0:dataWid-1])
    lables.append(row[-1])
##设置训练函数
clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
                        hidden_layer_sizes=(14,14,30), random_state=1)
##开始训练数据
clf.fit(xList, lables)
##读取预测值
y_pred=clf.predict(xList)
m = len(y_pred)

t = 0
f = 0
##预测结果分析
for i in range(m):
    if int(y_pred[i]) == lables[i]:
        t += 1
    else :
        f += 1
print("正确:"+str(t))
print("错误:"+str(f))

5.BP神经网络的缺点 

1）容易形成局部极小值而得不到全局最优值。BP神经网络中极小值比较多，所以很容易陷入局部极小值，这就要求对初始权值和阀值有要求，要使得初始权值和阀值随机性足够好，可以多次随机来实现。
      2）训练次数多使得学习效率低，收敛速度慢。
      3）隐含层的选取缺乏理论的指导。
      4）训练时学习新样本有遗忘旧样本的趋势。(可以把最优的权重记录下来)