js模拟栈---汉诺塔

	var Stack = (function(){
		var items = new WeakMap();
		//先入后出，后入先出
		class Stack{
			constructor(){
				items.set(this,[]);
			}
			push(ele){
				//入栈
				var ls = items.get(this);
				var len = ls.length;
				if(len > 0 &&  ls[len-1] <= ele){
					throw new Error("汉罗塔错误")
					return ;
				}
				ls.push(ele);
			}
			pop(){
				//出栈
				var ls = items.get(this);
				return ls.pop();
			}
			size(){
				//获取栈的长度
				var ls = items.get(this);
				return ls.length;
			}
			print(){
				//打印栈
				var ls = items.get(this);
				return ls.toString();
			}
		}
		return Stack;
	})();
 
	var stack1 = new Stack();
	var stack2 =new Stack();
	var stack3 = new Stack();
 
	const num = 3;  //汉诺塔的级数  
 
	for(var i = num; i >= 1; i-- ){
		stack1.push(i);
	}
	var obj = {
		"A":stack1,
		"B":stack2,
		"C":stack3
	}
	function hanoi(disc,a,b,c){
	    if(disc>0){
	        hanoi(disc-1,a,c,b);
	        console.log(' 移动 '+ disc +  ' 号圆盘 ' + ' 从 ' + a +  ' 移动到 ' +  c);
	        obj[c].push(obj[a].pop()); //转移数组
	        hanoi(disc-1,b,a,c);
	    }
	}
 
	//开始之前
	console.log(stack1.print());
	console.log(stack2.print());
	console.log(stack3.print());
	console.log("------------------------------"); 
 
	hanoi(obj["A"].size(),"A","B","C");
 
	//结果
	console.log(stack1.print());
	console.log(stack2.print());
	console.log(stack3.print());

"汉诺塔"是印度的一个古老传说，也是程序设计中的经典的递归问题，是一个著名的益智游戏：

　　题目如下：

　　　　塔上有三根柱子和一套直径各不相同的空心圆盘，开始时源柱子上的所有圆盘都按从大到小的顺序排列。目标是通过每一次移动一个圆盘到另一根柱子上，最终把一堆圆盘移动到目标柱子上，过程中不允许把较大的圆盘放置在较小的圆盘上；

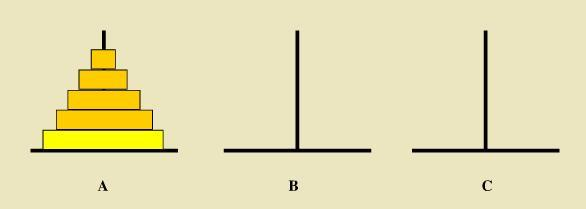
寻找规律（把所有的圆盘移动到C）：

　　1）n(圆盘个数) == 1

　　　　第一次：1号盘 A -> C sum(移动次数) = 1

　　2）n == 2

　　　　第一次：1号盘 A -> B

　　　　第二次：2号盘 A -> C

　　　　第三次：1号盘 B -> C　　sum = 3

　　3）n == 3

　　　　第一次：1号盘 A -> C

　　　　第二次：2号盘 A -> B

　　　　第三次：1号盘 C -> B

　　　　第四次：3号盘 A -> C

　　　　第五次：1号盘 B -> A

　　　　第六次：2号盘 B -> C

　　　　第七次：1号盘 A -> C　　sum = 7

　　以此类推...

　　故不难发现规律,移动次数为：sum = 2^n - 1　

算法分析（递归）：

　　把一堆圆盘从一个柱子移动另一根柱子，必要时使用辅助的柱子。可以把它分为三个子问题：

　　　　首先，移动一对圆盘中较小的圆盘到辅助柱子上，从而露出下面较大的圆盘，

　　　　其次，移动下面的圆盘到目标柱子上

　　　　最后，将刚才较小的圆盘从辅助柱子上在移动到目标柱子上

　　把三个步骤转化为简单数学问题：

　　　　（1）把 n-1个盘子由A 移到 B；

　　　　（2）把第 n个盘子由 A移到 C；

　　　　（3）把n-1个盘子由B 移到 C；

　例如:有A上有4个盘子
　　　　(1) 把 1-3由 A 移动到 B
　　　　(2) 把 4 由 A 移动到 C
　　　　(3) 把 1-3 由 B 移动到 C

　那么当A有100个盘子的时候

　　函数 hanoi 会就相当于一个大哥（入口），在100的时候，他告诉后面的小弟（回调），你帮我解决上面的1-99搬运好位置，这个小弟(回调)，又找自己下面的小弟(回调)，处理一下 1-88...这样回调下去，最后就变成最简单的单个移动问题了

　　我们创建一个JS函数，当它调用自身的时候，它去处理当前正在处理圆盘之上的圆盘。最后它回一个不存在圆盘去调用，在这种情况下，它不在执行任何操作。