从零开始一起学习SLAM | 神奇的单应矩阵

小白最近在看文献时总是碰到一个奇怪的词叫“homography matrix”，查看了翻译，一般都称作“单应矩阵”，更迷糊了。正所谓：“每个字都认识，连在一块却不认识”就是小白的内心独白。查了一下书上的推导，总感觉有种“硬凑”的意味，于是又找到了师兄。。。

神奇的单应矩阵
小白：师兄~单应矩阵是什么鬼啊？我看书上的推导，每一步勉强能看懂，但还是不太理解其背后的物理意义，感觉不能转化为自己理解的方式啊
师兄：哦，我第一次看的时候也是这种感觉

小白：而且这个名字好绕口啊，我完全没法和它的物理意义联系起来
师兄：这个名字是直接翻译的，是有点拗口，不过熟悉了也就还好。这个单应矩阵还是挺重要的

小白：师兄，能不能一句话告诉我单应矩阵是干嘛的啊
师兄：嗯，我的理解是：单应矩阵描述的就是同一个平面的点在不同图像之间的映射关系，这里前提是同一个平面，这个前提很重要

小白：还是不太懂啊，为什么要在不同图像之间进行映射呢？这样映射有什么用呢？为什么强调是同一个平面？
师兄：先别急，我一个个来说。我们先来看单应矩阵应用的一个例子。比如现在支付宝，微信都能通过对银行卡拍照自动识别银行卡号码，但是一般我们拍照时银行卡都不一定是正对着相机，可能会比较偏，比如像这样

但是你对着银行卡拍完照之后，你会发现这些软件会自动把银行卡抠出来，并且校正成非常规则的矩形，像下面这样

这样，识别银行卡数字的时候也方便多啦！

小白：我用过这个功能哎，这里面哪一步用到单应矩阵啦？
师兄：单应矩阵能够实现自动把银行卡从背景里“提取”出来，并且变成非常规整的矩形。你想想我前面说的单应矩阵描述的是同一个平面的点在不同图像之间的映射关系

小白：这个银行卡是一个平面，所以满足“同一个平面的点”的要求，那不同图像就是指拍摄的原始图像和校正过的图像咯？
师兄：正解！通过单应矩阵就能完成上述功能，还有其他类似的例子，比如有些手机里的小软件实现拍摄纸质的名片、投影的PPT等自动校正为矩形的功能，完全一样的道理。

小白：原来如此，单应矩阵这么厉害呢！
师兄：这个只是最基础的功能，实际上，单应矩阵还有非常多的应用。比如用于虚拟广告牌，这是很多重大赛事中很常见。比如下面是一个原始的图片。

我们想要把那个屏幕替换为“计算机视觉life”公众号的logo，用单应矩阵很轻松就能实现，你看下面是我们替换的结果，是不是很有趣？

小白：好好玩啊！突然开始喜欢单应矩阵啦！
师兄：除了这些，单应矩阵还有几个很重要的应用，一个是相机标定，比如张正友相机标定法，那个标定板不就是一个平面图案嘛！如下图所示

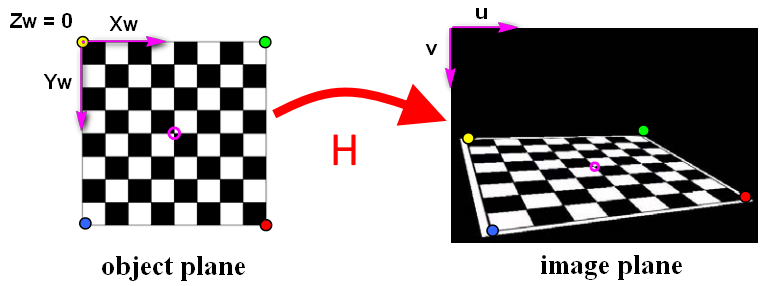
另外一个是单应矩阵还可以用于图像拼接，如下图所示。

还有现在很火的增强现实（AR），我们用平面二维标记图案（marker）来做AR展示的触发。我们根据单应矩阵就可以知道marker不同视角下的图像，这样可以方便的得到虚拟物体的位置姿态并进行显示，如下图所示。

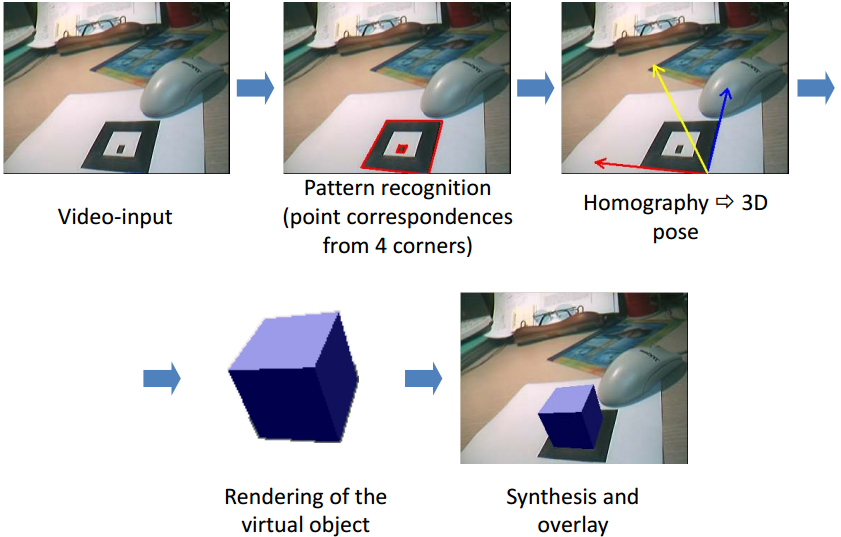
小白：真是开了眼界了！师兄，我已经迫不及待的要学习单应矩阵了！

快速理解单应矩阵
师兄：哈哈，单应矩阵的计算一般都会提供函数调用，我就简单说说单应矩阵是怎么来的，有哪些需要注意的地方
小白：好，师兄尽量通俗一点啊

师兄：嗯，你看下面这个图，两个不同的相机拍摄同一个平面

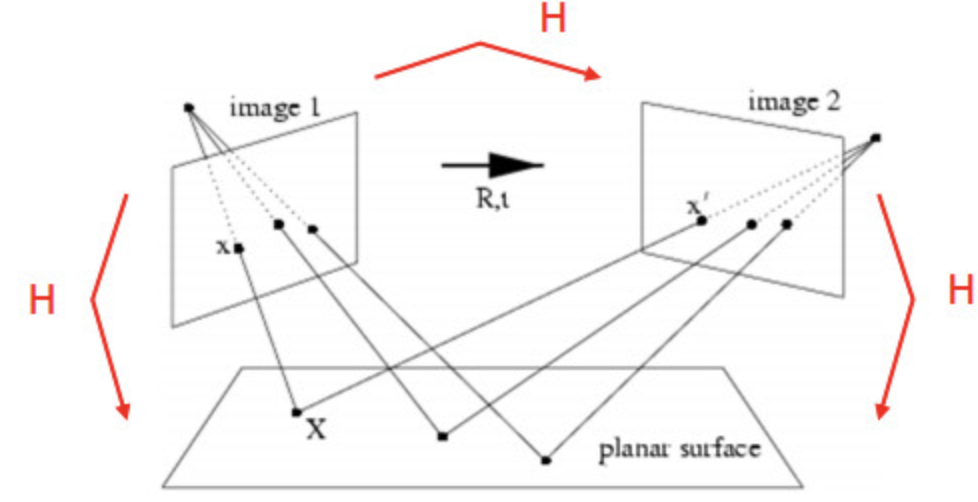
你还记得相机成像模型《从零开始一起学习SLAM | 相机成像模型》那一节中我们最后给的公式吗？
小白：记得，就是下面这个式子，其中，Puv(u, v,1)是图像中的像素坐标， Pw(xw, yw, zw，1) 是世界坐标系中的一个点，K是内参矩阵，R是旋转矩阵，t是平移向量，它们一起写成矩阵形式是 T，称为外参矩阵，表示从世界坐标系到相机坐标系的变换。

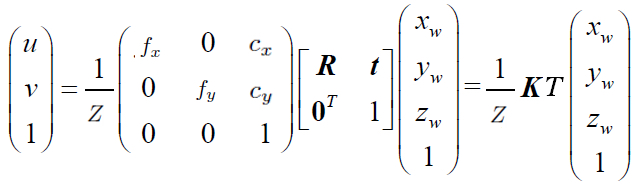
师兄：很好！现在我们简化一下表达形式，把中间部分记做M矩阵，如下

M矩阵是一个4 x 4 的矩阵，如果空间点在同一个平面上的话，我们可以看做 zw = 0，这样M矩阵就变成了一个 3 x 3的矩阵，对于两个不同的相机，像素坐标和空间点坐标可以写成如下的表示，其中M是3 x 3的矩阵

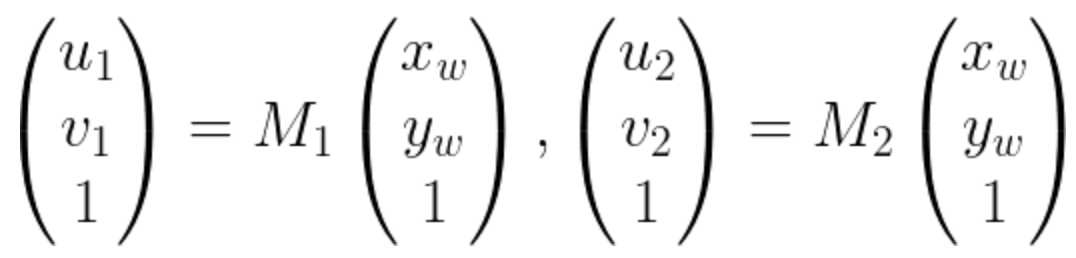
我们把上面两个式子合并一下就得到了下面这个式子，其中的H就是单应矩阵啦！H矩阵的两边是两张图像对应的匹配点对。也就是说单应矩阵H把三维空间中同一平面的点在两个相机的成像图片坐标进行了映射。

小白：原来如此~书上的推导为什么非要把1用平面方程来代替呢？
师兄：是为了增加空间点都是在平面的约束，本质上也是为了降维，把秩为4的矩阵降维成秩为3

小白：嗯嗯，上面的式子就是两个图像上的匹配的点对的映射吧
师兄：对的，如果展开，你会发现一个式子对应2个方程。也就是两个约束项。而单应矩阵本身自由度为8，所以只需要4个匹配点对就行啦

小白：等等，师兄，为啥单应矩阵H自由度为8？
师兄：这是因为等式两边都是齐次坐标，所以可以进行任意尺度的缩放。因此一般都会对H进行归一化，比如把最后一个元素设置为1，或者使得H矩阵所有元素的二范数为1

小白：明白啦，这样理解容易多了。
师兄：嗯，为了加深你的理解，给你布置一个作业，很有趣的作业哦，就是实现一下前面的虚拟广告牌
小白：好，今天的作业挺有意思~

作业
题目：
利用OpenCV编程实现虚拟广告牌的效果。提供两张图，一张是“计算机视觉life”公众号的logo，另外一张是带广告牌的原图，请用单应矩阵实现将原图中广告牌替换为提供的logo的效果。要求通过鼠标点击来选择要替换的广告牌的四个顶点。参考结果：

师兄提醒：关注“计算机视觉life”微信公众号，菜单栏回复“广告牌”，就能下载代码框架和图片啦！
原文链接：从零开始一起学习SLAM | 神奇的单应矩阵

相关阅读
从零开始一起学习SLAM | 为什么要学SLAM？
从零开始一起学习SLAM | 学习SLAM到底需要学什么？
从零开始一起学习SLAM | SLAM有什么用？
从零开始一起学习SLAM | C++新特性要不要学？
从零开始一起学习SLAM | 为什么要用齐次坐标？
从零开始一起学习SLAM | 三维空间刚体的旋转
从零开始一起学习SLAM | 为啥需要李群与李代数？
从零开始一起学习SLAM | 相机成像模型
从零开始一起学习SLAM | 不推公式，如何真正理解对极约束?
零基础小白，如何入门计算机视觉？

---------------------
作者：electech6
来源：CSDN
原文：https://blog.csdn.net/electech6/article/details/84101570
版权声明：本文为博主原创文章，转载请附上博文链接！