topcoder srm 540 div1

problem1 link

设第一个数字为$x$，那么第２到第$n$个数字都可以表示成$a+bx$的形式，其中$b=1$或者$b=-1$．然后可以求出关于$x$的一些范围，求交集即可．

problem2 link

设$f[i][r][g][b]$表示前$i$个已经染色完毕，第$i$颜色为$(r,g,b)$的概率．假设由$(r,g,b)$可以转移到的状态个数为$T$,那么每个可以转移到的状态$(r^{'},g^{'},b^{'})$都可以得到$\frac{f[i][r][g][b]}{T}$的贡献．暴力转移的复杂度太高．如果没有$d_{1}$的限制，那么$r,g,b$可以转移到的状态，如果将其看作三维空间中的坐标，是以$(r,g,b)$为中心的边长为$2d_{2}+1$的立方体．这样的更新可以整块进行．有了$d_{1}$，可以将至少有一个大于等于$d_{1}$改为所有的情况减去都小于$d_{1}$的情况．这样的话，$r,g,b$可以转移到的状态为以$r,g,b$为中心的边长为$2d_{2}+1$的立方体去掉以$r,g,b$为中心的边长为$2d_{1}+1$的立方体．

problem3 link

首先，由于10=2*5．这样将问题分解为计算模２以及模５的种类数．然后乘起来即可．考虑计算这个子问题．令$p=2$或者$5$．

由于如果$output[i]=0$，那么对应的区间一定有至少一个０，反之，一定是一个０也不会有．那么可以将$N$个数字分成两部分，一定不会出现0的部分以及可能有０的部分．

（１）对于可能有０的部分的计算：设$f[i][j]$表示放置了前$i$个数字，最后一个放置０的位置在$j$的方案数．

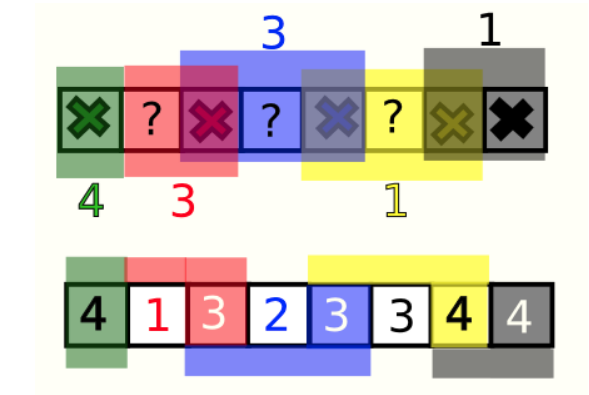
（２）对于一定没有０的部分的计算：首先，如果两个不同的区间$[L_{1},R_{1}],[L_{2},R_{2}]$的关系是$L_{1}=L_{2}$或者$R_{1}=R_{2}$，那么可以将其中一个较大的区间强行分成两段．这样最后所有的区间的两两之间的关系一定以下三种：不相交，一个是另一个的真子集，相交但是不是真子集．如下图所示，有绿，红，蓝，黄，黑５个区间．对于每个区间来说，如果区间内前面的元素确定了，那么区间的最后一个元素就是唯一的（因为$p$是素数）．这样的话，只有问号的位置是可以随意放置的．

code for problem1

#include <vector>
#include <string>
#include <limits>
using namespace std;

class ImportantSequence {
 public:
  int getCount(vector<int> B, string operators) {
    int64_t left = 1;
    int64_t right = std::numeric_limits<int64_t>::max();
    int64_t a = 0;
    int b = 1;
    for (size_t i = 0; i < B.size(); ++i) {
      int64_t val = static_cast<int64_t>(B[i]);
      if (operators[i] == '+') {
        a = val -a;
        b = -b;
      } else {
        a = a - val;
      }
      if (b == 1) {
        left = std::max(left, 1 - a);
      } else {
        right = std::min(right, a - 1);
      }
      if (left > right) {
        return 0;
      }
    }
    if (right == std::numeric_limits<int64_t>::max()) {
      return -1;
    }
    return static_cast<int>(right - left + 1);
  }
};

　　

code for problem2

#include <algorithm>
#include <cstring>
#include <iostream>

const int MAXN = 40;
const int MAX = 50;
double f[MAXN][MAX + 1][MAX + 1][MAX + 1];

class RandomColoring {
 public:
  double getProbability(int N, int maxR, int maxG, int maxB, int startR,
                        int startG, int startB, int d1, int d2) {
    this->max_r = maxR;
    this->max_g = maxG;
    this->max_b = maxB;
    f[0][startR][startG][startB] = 1;
    for (int i = 1; i < N; ++i) {
      for (int r = 0; r < maxR; ++r) {
        const std::pair<int, int> rd2 = ComputeRage(r, d2, maxR);
        const std::pair<int, int> rd1 = ComputeRage(r, d1 - 1, maxR);
        for (int g = 0; g < maxG; ++g) {
          const std::pair<int, int> gd2 = ComputeRage(g, d2, maxG);
          const std::pair<int, int> gd1 = ComputeRage(g, d1 - 1, maxG);
          for (int b = 0; b < maxB; ++b) {
            const std::pair<int, int> bd2 = ComputeRage(b, d2, maxB);
            const std::pair<int, int> bd1 = ComputeRage(b, d1 - 1, maxB);
            const int s1 = Size(rd2) * Size(gd2) * Size(bd2);
            const int s0 = d1 > 0 ? Size(rd1) * Size(gd1) * Size(bd1) : 0;
            if (s1 == s0) {
              continue;
            }
            const double e = f[i - 1][r][g][b] / (s1 - s0);
            Add(i, rd2.first, gd2.first, bd2.first, rd2.second, gd2.second,
                bd2.second, e);
            if (d1 > 0) {
              Add(i, rd1.first, gd1.first, bd1.first, rd1.second, gd1.second,
                  bd1.second, -e);
            }
          }
        }
      }
      for (int r = 0; r < maxR; ++r) {
        for (int g = 0; g < maxG; ++g) {
          for (int b = 0; b < maxB; ++b) {
            f[i][r][g][b] += Get(i, r - 1, g, b) + Get(i, r, g - 1, b) +
                             Get(i, r, g, b - 1) - Get(i, r - 1, g - 1, b) -
                             Get(i, r - 1, g, b - 1) - Get(i, r, g - 1, b - 1) +
                             Get(i, r - 1, g - 1, b - 1);
          }
        }
      }
    }
    double result = 0;
    for (int x = 0; x < maxR; ++x) {
      for (int y = 0; y < maxG; ++y) {
        for (int z = 0; z < maxB; ++z) {
          if (!(abs(x - startR) <= d2 && abs(y - startG) <= d2 &&
                abs(z - startB) <= d2 &&
                (abs(x - startR) >= d1 || abs(y - startG) >= d1 ||
                 abs(z - startB) >= d1))) {
            result += f[N - 1][x][y][z];
          }
        }
      }
    }
    return result;
  }

  double Get(int t, int x, int y, int z) {
    if (x >= 0 && y >= 0 && z >= 0) {
      return f[t][x][y][z];
    }
    return 0.0;
  }

  void Add(int t, int x, int y, int z, int x1, int y1, int z1, double val) {
    Add(t, x, y, z, val);
    Add(t, x, y, z1 + 1, -val);
    Add(t, x, y1 + 1, z, -val);
    Add(t, x1 + 1, y, z, -val);
    Add(t, x1 + 1, y1 + 1, z, val);
    Add(t, x1 + 1, y, z1 + 1, val);
    Add(t, x, y1 + 1, z1 + 1, val);
    Add(t, x1 + 1, y1 + 1, z1 + 1, -val);
  }
  void Add(int t, int x, int y, int z, double val) {
    if (x < max_r && y < max_g && z < max_b) {
      f[t][x][y][z] += val;
    }
  }

  std::pair<int, int> ComputeRage(int x, int d, int max_x) {
    return {std::max(0, x - d), std::min(x + d, max_x - 1)};
  }
  int Size(const std::pair<int, int> &range) {
    return range.second - range.first + 1;
  }

 private:
  int max_r, max_g, max_b;
};

　　

code for problem3

#include <string>
#include <vector>
#include <limits>
#include <iostream>
using namespace std;

class ProductQuery {
  static const int64_t mod = 1000000007;

 public:
  int theInput(int N, vector<int> Qfrom, vector<int> Qto, vector<int> output) {
    auto ModFunc = [output](const int p) -> std::vector<int> {
      std::vector<int> r;
      for (auto x : output) {
        r.push_back(x % p);
      }
      return r;
    };
    return static_cast<int>(Compute(N, Qfrom, Qto, ModFunc(2), 2) *
                            Compute(N, Qfrom, Qto, ModFunc(5), 5) %
                            mod);
  }

 private:
  int64_t Compute(int N, const std::vector<int> &qfrom,
                  const std::vector<int> &qto, const std::vector<int> &output,
                  const int p) {
    std::vector<int> not_zero(N, 0);
    for (size_t i = 0; i < output.size(); ++i) {
      if (0 != output[i]) {
        for (int j = qfrom[i]; j <= qto[i]; ++j) {
          not_zero[j] = 1;
        }
      }
    }
    int zero_index = 0;
    int not_zero_index = 0;
    std::vector<int> zero_map(N, -1);
    std::vector<int> not_zero_map(N, -1);
    for (int i = 0; i < N; ++i) {
      if (not_zero[i] == 0) {
        zero_map[i] = zero_index++;
      } else {
        not_zero_map[i] = not_zero_index++;
      }
    }
    std::vector<int> zero_qfrom;
    std::vector<int> zero_qto;
    std::vector<int> not_zero_qfrom;
    std::vector<int> not_zero_qto;
    std::vector<int> not_zero_output;
    auto FindValidRange = [](const std::vector<int> &elements, int left,
                             int right) -> std::pair<int, int> {
      int left_index = -1;
      int right_index = -1;
      for (int j = left; j <= right; ++j) {
        if (elements[j] != -1) {
          if (left_index == -1) {
            left_index = elements[j];
          }
          right_index = elements[j];
        }
      }
      return {left_index, right_index};
    };
    for (size_t i = 0; i < output.size(); ++i) {
      if (output[i] == 0) {
        auto r = FindValidRange(zero_map, qfrom[i], qto[i]);
        if (r.first == -1) {
          return 0;
        }
        zero_qfrom.push_back(r.first);
        zero_qto.push_back(r.second);
      } else {
        auto r = FindValidRange(not_zero_map, qfrom[i], qto[i]);
        if (r.first == -1) {
          return 0;
        }
        not_zero_qfrom.push_back(r.first);
        not_zero_qto.push_back(r.second);
        not_zero_output.push_back(output[i]);
      }
    }
    return Place0(zero_index, zero_qfrom, zero_qto, p) *
           NotPlace0(not_zero_index, not_zero_qfrom, not_zero_qto,
                     not_zero_output, p) %
           mod;
  }
  int64_t Place0(int N, const std::vector<int> &qfrom,
                 const std::vector<int> &qto, const int p) {

    if (N == 0) {
      return 1;
    }
    auto CheckForceZero = [qfrom, qto](int pre_zero_index,
                                       int cur_index) -> bool {
      for (size_t i = 0; i < qfrom.size(); ++i) {
        if (qfrom[i] > pre_zero_index && qto[i] == cur_index) {
          return true;
        }
      }
      return false;
    };
    auto EncodeIndex = [](int t) { return t + 1; };
    std::vector<std::vector<int64_t>> f(N, std::vector<int64_t>(N + 1, 0));
    f[0][EncodeIndex(0)] = 1;
    if (!CheckForceZero(-1, 0)) {
      f[0][EncodeIndex(-1)] = p - 1;
    }
    for (int i = 1; i < N; ++i) {
      for (int j = -1; j < i; ++j) {
        const int64_t val = f[i - 1][EncodeIndex(j)];
        Add(f[i][EncodeIndex(i)], val);
        if (!CheckForceZero(j, i)) {
          Add(f[i][EncodeIndex(j)], val * (p - 1) % mod);
        }
      }
    }
    int64_t result = 0;
    for (int i = -1; i < N; ++i) {
      Add(result, f[N - 1][EncodeIndex(i)]);
    }
    return result;
  }
  int64_t NotPlace0(int N, const std::vector<int> &qfrom,
                    const std::vector<int> &qto, const std::vector<int> &output,
                    const int p) {
    if (N == 0) {
      return 1;
    }
    std::vector<int64_t> rev_table(p);
    for (int i = 1; i < p; ++i) {
      for (int j = 1; j < p; ++j) {
        if (i * j % p == 1) {
          rev_table[i] = j;
          break;
        }
      }
    }
    std::vector<bool> delete_items(output.size(), false);
    std::vector<int> last_qfrom = qfrom;
    std::vector<int> last_qto = qto;
    std::vector<int> last_output = output;
    bool updated = true;
    int total_range = static_cast<int>(output.size());
    while (updated) {
      updated = false;
      for (size_t i = 0; i < output.size(); ++i) {
        if (!delete_items[i]) {
          for (int j = i + 1; j < output.size(); ++j) {
            if (!delete_items[j]) {
              if (last_qfrom[i] == last_qfrom[j] && last_qto[i] == last_qto[j]) {
                if (last_output[i] != last_output[j]) {
                  return 0;
                }
                --total_range;
                delete_items[j] = true;
                updated = true;
              } else if (last_qfrom[i] == last_qfrom[j]) {
                if (last_qto[i] < last_qto[j]) {
                  last_qfrom[j] = last_qto[i] + 1;
                  last_output[j] =
                      last_output[j] * rev_table[last_output[i]] % p;
                } else {
                  last_qfrom[i] = last_qto[j] + 1;
                  last_output[i] =
                      last_output[i] * rev_table[last_output[j]] % p;
                }
                updated = true;
              } else if (last_qto[i] == last_qto[j]) {
                if (last_qfrom[i] < last_qfrom[j]) {
                  last_qto[i] = last_qfrom[j] - 1;
                  last_output[i] =
                      last_output[i] * rev_table[last_output[j]] % p;
                } else {
                  last_qto[j] = last_qfrom[i] - 1;
                  last_output[j] =
                      last_output[j] * rev_table[last_output[i]] % p;
                }
                updated = true;
              }
            }
          }
        }
      }
    }
    int64_t result = 1;
    for (int i = 1; i <= N - total_range; ++i) {
      result = result * (p - 1) % mod;
    }
    return result;
  }
  void Add(int64_t &x, int64_t y) {
    x += y;
    if (x >= mod) {
      x -= mod;
    }
  }
};