Computer Vision_33_SIFT：SAR-SIFT: A SIFT-LIKE ALGORITHM FOR SAR IMAGES——2015

此部分是计算机视觉部分，主要侧重在底层特征提取，视频分析，跟踪，目标检测和识别方面等方面。对于自己不太熟悉的领域比如摄像机标定和立体视觉，仅仅列出上google上引用次数比较多的文献。有一些刚刚出版的文章，个人非常喜欢，也列出来了。

33. SIFT
关于SIFT，实在不需要介绍太多，一万多次的引用已经说明问题了。SURF和PCA-SIFT也是属于这个系列。后面列出了几篇跟SIFT有关的问题。
[1999 ICCV] Object recognition from local scale-invariant features
[2000 IJCV] Evaluation of Interest Point Detectors
[2006 CVIU] Speeded-Up Robust Features (SURF)
[2004 CVPR] PCA-SIFT A More Distinctive Representation for Local Image Descriptors
[2004 IJCV] Distinctive Image Features from Scale-Invariant Keypoints
[2010 IJCV] Improving Bag-of-Features for Large Scale Image Search
[2011 PAMI] SIFTflow Dense Correspondence across Scenes and its Applications

[2015 TGRS] SAR-SIFT: A SIFT-LIKE ALGORITHM FOR SAR IMAGES

[2017 GRSL] Remote Sensing Image Registration With Modified SIFT and Enhanced Feature Matching

翻译

SAR-SIFT：一种类似于SAR图像的SIFT算法——

作者：Flora Dellinger, Julie Delon, Yann Gousseau, Julien Michel, Florence Tupin

https://hal.archives-ouvertes.fr/hal-00831763

HAL是一个多学科的开放获取档案库，用于保存和分发科学研究文献(无论是否出版)。 这些文件可能来自法国或国外的教学和研究机构，也可能来自公共或私人研究中心。HAL的原始档案馆，以及DES的科学文献，出版了非官方的，法国的共和国和法国的公共刊物，以及私人的实验室。

摘要 -尺度不变特征变换(SIFT)算法广泛用于计算机视觉中，以匹配图像之间的特征或定位和识别对象。 但是，主要是由于斑点噪声，所以在合成孔径雷达(SAR)图像上效果不佳。 我们在这里提出了一种针对SAR图像的算法，称为SAR-SIFT。首先介绍了一种新的梯度计算方法，该方法可产生方向性和对斑点噪声具有鲁棒性的幅度。 然后将其用于将SIFT算法的多个步骤适配到SAR图像。与现有方法相比，我们研究了这种新算法带来的改进。 我们提出了SAR-SIFT在不同配置(尤其是具有不同入射角)的SAR图像配准中的应用。

索引词-合成孔径雷达(SAR)，遥感，SAR图像配准，尺度不变特征变换(SIFT)

Ⅰ 引言

在光学和合成孔径雷达(SAR)领域中，最新一代的地球观测卫星都提供了大量的高分辨率数据，从而导致了多传感器，多分辨率和/或多角度情况的发展。为了共同利用这些数据进行分类，3D重建，快速映射或更改检测，具有某些特定不变性的基于特征的方法可能比基于像素的方法更为合适。本文特别研究了基于特征的描述符对SAR数据的兴趣。

尺度不变特征变换(SIFT)[1]是用于兴趣点检测和局部特征描述的非常经典的算法。由于其效率[2]，它被广泛用于计算机视觉领域，以定位和识别图像之间的对象。它对于比例尺变化，旋转，平移以及光照变化和仿射失真的不变性使其适合于不同类型的应用，例如对象检索，图像索引，缝合，配准或视频跟踪。

SIFT算法由于其性能和不变性而成为遥感图像的一个有趣的选择。该算法主要应用于光学图像，因为它们具有类似于自然图像的特征。几种配准方法[3]，[4]，[5]使用SIFT关键点作为控制点(CP)来估计变形模型。 Li [3]考虑了遥感图像的特殊性，并引入了一种新的匹配标准，该标准具有比例和方向限制。 Huo [4]提出了一种多级SIFT匹配方法，借助随机样本共识(RANSAC)来配准非常高分辨率的图像。Sedaghat [5]使该算法适应以获得空间均匀分布的关键点，并通过应用投影模型来过滤不匹配项。 SIFT算法还有一些资产可用于遥感图像检索或分类应用。Yang [6]使用SIFT描述符的词袋(BoW)表示法在高分辨率图像中进行土地利用/土地覆盖分类的图像检索。 Risojevic [7]通过合并Gabor纹理描述符和SIFT描述符BoW的表示来执行图像分类。对象检测是SIFT算法的另一个应用领域。Sirmacek [8]通过使用SIFT关键点，多个子图匹配和图切割方法，在高分辨率的光学图像上检测到单个建筑物。 Tao [9]通过考虑聚类的SIFT关键点和区域分割来执行机场检测。

尽管SIFT算法已经证明了其在光学遥感中的各种应用的效率，但SAR图像的情况却有所不同。 SAR是一个主动系统，其优点是可以独立于天气条件和太阳光照获取图像。 SAR图像经常在灾难情况下使用，因为它们通常是最快的可用图像。然而，图像被称为斑点的强乘法噪声破坏，因此使数据处理变得困难。 SIFT算法在此类图像上效果不佳。已经提出了一些改进来改进算法。有人建议对图像进行预滤波[10]或去噪[11]，以减少斑点噪声的影响。其他人则删除一些不变性[12]，[13]或修改算法[14]，[15]的某些步骤以提高性能。 Lv [16]和Fan [17]考虑关键点之间的空间关系以抑制错误对应。为了限制搜索空间，Wessel [18]使用DEM和轨道信息，而Xiaoping [19]执行手动预配准。这些算法的详细信息和局限性将在II-C节中介绍。然而，这些新开发的算法的性能仍然相对有限，并且正确匹配的数量不足以考虑配准以外的其他应用。他们中的大多数没有考虑斑点噪声的统计特异性。考虑到SIFT算法在光学图像中提供的应用领域，拥有一种适用于SAR图像的，类似于SIFT的高性能算法将非常令人感兴趣。

我们在本文中提出将SIFT算法适应SAR图像的统计特异性。第二部分介绍了经典SIFT算法的概述及其在SAR图像上的行为。第三部分介绍了新的梯度计算和类似于SIFT的算法，两者都适用于SAR图像。实验验证和性能在第四节中介绍。最后，第五节研究了这种新算法为SAR成像中的多角度和多分辨率环境提供的可能性。介绍了SAR图像配准的应用和变化检测的初步结果。

这项工作的会议记录版本已经出现在[20]中。

Ⅱ SAR图像上SIFT算法和行为的表示

在本节中，将介绍原始的SIFT算法及其一些变体。当应用于SAR图像时，我们还介绍了它的局限性，以及为应对此类图像而进行的一些调整。

A.原始SIFT算法的介绍
Lowe于2004年[1]引入了SIFT算法来匹配自然图像中的局部特征。该算法遵循四个步骤，我们将在以下段落中进行描述：

1)关键点检测：选择第一个关键点作为局部兴趣点，并通过其局部化(x，y)，比例σ和方向θ进行表征：
P(x，y，σ，θ)

作为高斯(LoG)拉普拉斯算子(LoG)[21]的近似值，高斯(DoG)尺度空间的差异由尺度σ_l=σ₀·r^l 和l∈|| 0..l_max-1 ||构成 。然后选择三个维度(x，y，σ)中的局部极值，以获得由其位置和比例定义的关键点。

具有低对比度或位于边缘的候选对象将根据基于Hessian矩阵的标准进行过滤[1]。另一种可能性是使用基于哈里斯矩阵的多尺度哈里斯角检测器[22]。

在其他兴趣点检测器中，我们可以引用HarrisLaplace [23]，该点将空间中的点定位为多尺度Harris函数的极值，而将尺度定位为LoG的最大值。通过用Hessian行列式的局部最大值代替空间选择，Hessian-Laplace [24]实现了更精确的定位。为了实现仿射不变性，Harris-Affine [25]和Hessian-Affine [24]检测器通过基于二阶导数矩阵的迭代自适应来优化定位。 ASIFT [26]模拟不同的视点以评估两个相机轴方向参数。

在本文中，我们将比较提出的关键点检测方法(请参阅第III-B1节)与在LoG尺度空间中检测为局部极值(在(x，y，σ)中)的关键点。这些点将通过多尺度哈里斯准则进行过滤，以消除那些位于边缘或低对比度的点。我们将这种方法称为LoG方法。

2)方向分配：为了确定与关键点相关的主要方向，Lowe [1]建议计算梯度方向加权的局部梯度直方图。直方图是在与比例相关的邻域上计算的。主要方向定义为高于最大80％的箱柜。在[27]中，直方图被在x和y方向上的Haar小波响应所代替，并且在滑动方向窗口内计算响应的总和以估计主方向。

在本文[28]之后，由于采用了逆向方法，我们选择了局部方向直方图的主要模式。与原始SIFT算法一样，可以使用相同的位置和比例但具有不同的方向θ获得不同的关键点。

3)描述符提取：将SIFT描述符分配给每个关键点P(x，y，σ，θ)以描述其局部几何形状。在每个点周围定义一个正方形邻域，其大小取决于σ，以获得平移和尺度不变性。然后将其旋转一个角度-θ以确保旋转不变性。将该归一化的邻域划分为4×4的正方形扇区，在该扇区上计算梯度方向的直方图(由梯度大小加权)。对于每个关键点，SIFT描述符是通过将这些直方图进行级联和标准化而获得的。

在文献中已经提出了SIFT描述符的不同改编。 PCA-SIFT [29]是通过在标准化梯度邻域上应用PCA获得的。 GLOH [2]在对数极坐标网格上和17个扇区上计算，所得向量的大小通过PCA减小。 SURF [27]是通过用垂直和水平方向的Haar小波响应之和代替梯度直方图获得的。

在这里，我们选择将SIFT描述符与9个扇区的对数极坐标网格[28]一起使用(图11)。

4)关键点匹配：两个不同图像的关键点根据它们各自的描述符进行匹配。文献中存在不同的匹配标准，但最常用的是最近邻距离比(NNDR)方法[1]。首先，计算一个描述符与另一个图像之间的欧几里得距离，并选择最近的邻居。为了过滤错误匹配，比较到第二个和第一个最近邻居的距离。将阈值th应用于这些相应距离的比率。我们将第一步称为最近邻居(NN)步，将第二步称为距离比(DR)步。

在[28]中，使用反向方法对所有可能的匹配计算出误报的概率。这种方法允许对一个关键点进行不同的匹配，并允许识别一个对象的多次出现。

为了简单起见，此处将使用NNDR方法。

B. SIFT算法对SAR图像的局限性

图1：将LoG关键点检测方法的结果应用于斑点噪声和1幅幅度图像损坏的矩形(检测到29个关键点)。

SIFT算法在SAR图像上效果不佳。发生许多错误的关键点检测以及错误的匹配。特别是，斑点噪声会导致使用LoG方法(图1)进行大量错误检测。在光学图像上，噪声通常相对较弱，该算法的关键点过滤部分(多尺度哈里斯准则[22])由于其对比度依赖性而抑制了大多数错误检测。
然而，SAR图像呈现出较大的动态范围，并且乘性噪声导致具有高反射率的均匀区域上的梯度幅度更大(图2(b))。因此，就不会抑制高对比度区域上的虚假警报，如斑点噪声损坏的矩形示例所示(见图1)。

方向和描述符对于乘性噪声也不强健，因为它们的计算依赖于经典的差异梯度。

C. SIFT算法对SAR图像的先前改编

在文献中已经提出了针对SAR图像的SIFT算法的修改。有些人建议通过跳过用于关键点检测的最小标度[12]或通过抑制方向分配[13]，[17]来简化算法。尽管这样的程序确实减少了错误检测的次数，因为许多错误检测发生在那些规模上，但其余关键点仍未精确定位。
抑制方向限制了算法匹配具有不同观看条件的图像的能力。

为了改进算法，可以调整一些步骤。
在[15]中，对强度值进行阈值化以获得空间上均匀分布的关键点，并扩展区域描述符的大小以提高匹配性能。但是，这限制了描述符的区别性，并阻止了算法在变化较大的图像上的应用。在[14]中，具有渐进式下采样的新金字塔用于关键点检测，而SIFT描述符被Shape Context的改进版本取代。这种新算法虽然速度更快，但其性能却比原始SIFT低。

一些工作建议通过用各向异性的[30]或通过计算多视点[19]，[18]代替高斯尺度空间来减少散斑的影响。但是，最后一个过程降低了图像分辨率，并导致信息丢失。另一个解决方案是对图像去噪：可以使用Curvelet变换[10]或无限对称指数滤波器(ISEF)[11]。去噪非常耗时，并且会产生干扰算法的伪像。虽然这些算法的性能要比直接应用于SAR图像的原始SIFT算法要好，但正确匹配的次数通常很少(几十个数量级)。

其他研究建议通过排除异常值来提高性能。 Lv [16]将图像划分为四个子区域，并考虑每个子区域中匹配关键点的空间关系。但是，这意味着图像表示相同的场景，几乎没有重叠且没有旋转。对于配准应用，在[17]中基于最佳对应关系估计了图像变换，但使用了限制性变形。 Wu [31]结合了SIFT算法和聚类奖励相似性度量来迭代估计仿射变换。该过程很耗时，并且仅限于图像配准。

可以通过执行手动预配准来限制搜索空间[19]。可以通过知道轨道信息(即使不精确)来消除错误的对应关系[18]，以及数字高程模型(DEM)。但是，这类信息并非总是已知的，手动预配准非常耗时，并且容易出现解释错误。

为了使SIFT算法适合SAR图像，必须考虑SAR图像的统计特性。我们建议首先开发一种新的梯度计算，这要归因于其幅度和方向都对斑点噪声具有鲁棒性。然后，算法的几个步骤可以适应SAR图像。引入了新的关键点检测方法，以及新的方向分配和SAR自适应描述符。关键点匹配步骤没有修改，因为它在很大程度上不取决于图像的类型，而是取决于描述符的质量。第三节介绍了这些新发展。

图2：两种斑点计算方法在斑点噪声和其梯度幅度所破坏的矩形的示例。

Ⅲ 建议的方法

A.SAR图像的梯度计算

1)最新技术：许多边缘检测工作都强调了在SAR图像上通过差异使用梯度的问题。实际上，梯度分量的变化取决于底层的反射率[32]。边缘检测的传统方法在于对梯度幅度进行阈值化。对于SAR图像，与低反射率相比，在高反射率的同质区域中导致较高的误报率。因此，差分的经典梯度不是恒定的误报率运算符。统计研究[32]，[33]，[34]表明，使用比值比使用差异更适合乘法噪声。引入了几种使用比率的边缘检测器，以便在SAR图像上获得恒定的误报率：

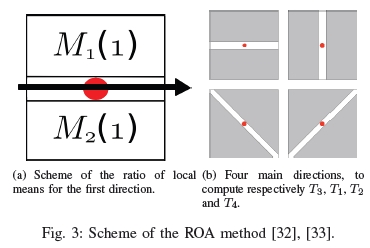
(a)第一方向的局部均值比例方案。
(b)四个主要方向，分别计算T3，T1，T2和T4。
图3：ROA方法的方案[32]，[33]。

•平均比率(ROA)[32]，[33]在于计算沿一个方向i(图3(a))在研究像素相对侧的局部均值比率：

然后将比率R_i归一化：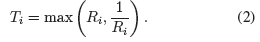

这些比率沿四个主要方向计算(图3(b))。梯度大小D_n¹和方向D_t¹定义为：

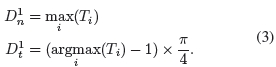
然后可以通过对梯度幅度D in进行阈值化来获得边缘。

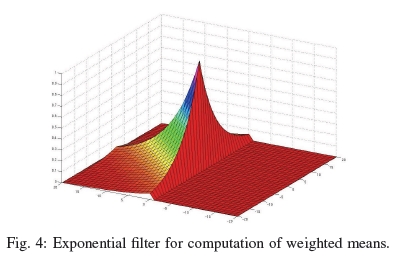
图4：用于计算加权均值的指数滤波器。

•指数加权平均比率(ROEWA)[35]是对多边缘上下文的ROA的改进，通过计算指数加权局部均值获得(图4)。例如，给定一个点(a，b)，垂直方向的均值定义为：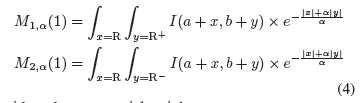

其中α为指数权重参数。

与ROA中一样，方向i的比率及其归一化定义为：

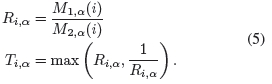
这些比率T_i,α是沿水平(i = 1)和垂直(i = 3)方向计算的。与基于梯度的光学图像上的边缘检测器类似，可以通过以下方式获得边缘图像：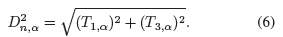

由于加权参数α允许对图像进行自适应平滑，因此ROEWA在多尺度边缘上下文中更为精确，并且比ROA更具抗噪性。

这些算子已经设计用于边缘检测，并且可以很好地估计梯度大小。但是，由于仅考虑了几个方向，因此它们没有给出梯度方向的精确度量。这可以通过增加方向数量来改善，但是会很费时间。

Suri [13]建议将垂直和水平梯度分别定义为T_1,α和T_3,α。类似于光学图像的基于梯度的边缘检测器，梯度的大小和方向估计为：

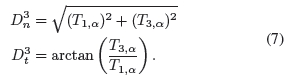
方向的定义非常值得怀疑。实际上，T_1,α和T_3,α始终取正值，因此D_t³只能取0到 π/ 2之间的值。此外，在具有反射率m_a和m_b(m_a <m_b)的垂直边缘上的梯度计算得出：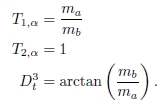

因此，梯度取向取决于区域的反射率而取任意值，而期望为零。归一化比率T_1,α和T_3,α不应直接用于计算梯度方向。

2)建议的方法：我们在此建议将水平和垂直渐变定义为：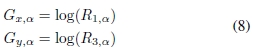

并以通常的方式计算梯度的大小和方向：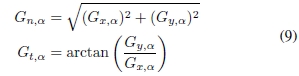

使用α的指数权重参数来计算局部均值。

通过使用对数，避免了上面提到的垂直边缘上的梯度方向问题，因为计算得出：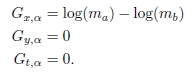

为了获得负梯度值和正梯度值，在比率及其倒数之间没有最小值(或最大值)的标准化。通过这种方法，可以考虑定向值的所有可能性。另外，由于加权参数α允许以不同的比例对图像进行平滑，因此可以将该梯度与通过对具有高斯模糊的图像施加的差进行比较。我们称这种新的梯度计算方法为“按比率梯度(GR)”。

图2给出了两种梯度计算方法在斑点噪声损坏的矩形上的梯度大小。比率梯度法(公式(8,9))在反射率高的区域上不会产生比反射率低的区域更高的值，这与按梯度进行梯度计算不同。

图5：入射角为34°，分辨率为1m的Cosmo-SkyMed R图像的提取。

图6：在图5的图像上应用σ= 2的高斯模糊产生的差异梯度。

图7：在α= 2的情况下应用于图5的图像的新梯度计算(按比率梯度)。

图5的图像的梯度值在图6中显示为差异梯度，在图7中显示为GR。似乎梯度差异可以更好地降低斑点噪声，但高反射率区域的梯度值(幅度以及垂直和水平分量)要比低反射率区域的梯度值高。但是，对于GR方法，在那些区域上梯度响应并不更高。

现在，这种新的梯度计算方法将帮助我们使SIFT算法适应SAR图像。

B.适用于SAR图像的类似于SIFT的算法

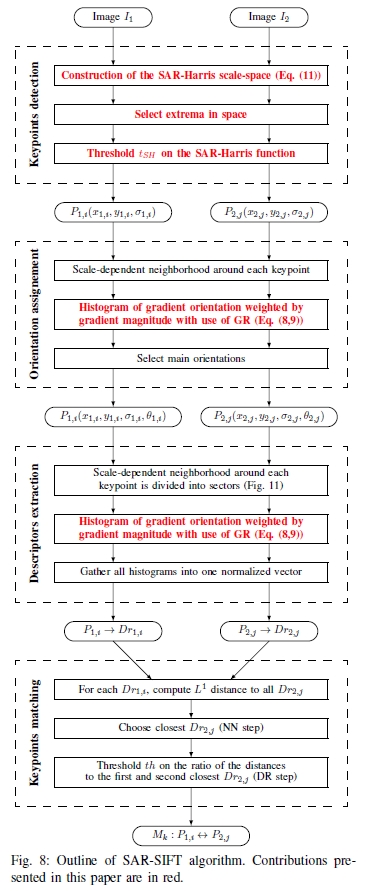
新算法的轮廓(我们称为SAR-SIFT)如图8所示。如前所述，该算法的前三个步骤适用于SAR图像，只有最后一个(匹配)保持不变。

---

图像I₁  图像I₂

→　　→
关键点检测
SAR-Harris比例空间的构造(式(11))→
选择空间极值 →
SAR-Harris函数的阈值t_SH →

→　　→

P_1,i(x_1,i，y_1,i，σ_1,i) P_2,j(x_2,j，y_2,j，σ_2,j)

→　　→
方向分配
每个关键点周围与比例相关的邻域 →
使用GR(梯度(8,9))由梯度量加权的梯度方向直方图 →
选择主要方向 →

→　　→
P_1,i(x_1,i，y_1,i，σ_1,i，θ_1,i) P_2,j(x_2,j，y_2,j，σ_2,j，θ_2,j)

→　　→
描述符提取
每个关键点周围与比例相关的邻域被划分为多个扇区(图11)→
使用GR(梯度(8,9))由梯度量加权的梯度方向直方图 →
将所有直方图收集到一个归一化向量中 →

→　　→
P_1,i→Dr_1,i   P_2,j→Dr_2,j

→　　→
关键点匹配
对于每个Dr_1,i，计算到所有Dr_2,j的L¹距离 →
选择最接近的Dr_2,j(NN步) →
到第一个和第二个最接近的Dr_2,j的距离之比的阈值th(DR步)→

→
 M_k(P_1,i，P_2,j)

---

图8：SAR-SIFT算法概述。 本文中的贡献为红色。

1)关键点检测：在SAR图像上检测关键点的第一种简单方法是将LoG方法应用于图像的对数。这允许处理加性噪声而不是乘性噪声，并抑制在高反射率区域上的错误检测。尽管由于其简单性而吸引人，但该方法对噪声的鲁棒性不足，并且不能大大提高原始LoG方法的性能(图1)。如图9(a)上的斑点噪声损坏的矩形示例所示，确实在关键点附近确实找到了关键点，但是位置很差。与直接应用在振幅图像上相比，错误检测更少(图1)，它们在高反射率区域和低反射率区域也同样发生，但仍然很多。通过调整多尺度哈里斯准则[22]的参数，可以减少错误检测的次数，但也可以减少正确检测的次数。

图9：使用图像对数上的LoG方法和SAR-Harris方法，检测斑点噪声损坏的矩形上的关键点。

LoG和Hessian矩阵似乎不方便且不容易适应乘法噪声，因为它们依赖于二阶导数。相反，多尺度哈里斯函数[23]基于一阶导数。根据我们在第III-A节中开发的适用于SAR图像的新梯度计算，我们提出了一种基于此检测器的新方法。

针对光学图像，将多尺度哈里斯矩阵和函数分别定义为：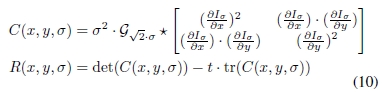

在G√2·σ为标准偏差为√2·σ的高斯核的情况下，⋆是卷积算子，I_σ是标准偏差为σ且参数为任意参数的高斯核对原始图像的卷积。请注意，这里需要权重σ²才能进行全面归一化[23]。在LoG方法中，多尺度哈里斯准则允许通过在R(x，y，σ)上应用阈值d_H来抑制低对比度和边缘点。

考虑到该定义和比率梯度，我们分别提出了新的SAR-Harris矩阵和多尺度SAR-Harris函数：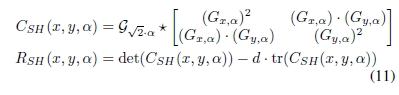

其中d为任意参数，并且使用等式(8)计算导数G_x,α和G_y,α。

在这种情况下，可以证明不再需要乘以σ²来确保尺度不变。

对于这种关键点检测方法，我们用原始图像的多尺度表示代替LoG尺度空间，该原始图像是通过在不同尺度α_k=α₀·c^m的情况下计算多尺度SAR-Harris函数(等式(11))而获得的其中m∈|| 0..m_max -1 ||。然后在每个级别上选择空间的局部极值作为要点候选。通过对局部极值执行SAR-Harris准则的双线性插值，可以精炼关键点的子像素位置。多尺度SAR-Harris函数上的阈值dSH可以过滤边缘和低对比度点。我们获得以其位置(x，y)和比例α为特征的关键点。

为了避免使用二阶导数，这种称为SAR-Harris方法的方法合并了LoG方法的两个步骤。由于易于验证，因此它还具有独立于图像对比度的优点。

我们已经注意到，这种比例空间很少达到3维的极值。在光学图像上也观察到了这一事实[23]。因此仅选择空间的极值。然后，可以在同一位置但以不同的比例进行几次检测。但是，通过对多尺度SAR-Harris函数设定阈值来抑制其中的一些。

图9(b)上被斑点噪声破坏的矩形示例显示了此方法的效率：关键点仅在拐角处发现，正如预期的那样，并且没有错误检测。

图10：采用LoG方法检测图5图像上的关键点，并将其应用于振幅图像和图像的对数，以及SAR-Harris方法。 调整阈值dH和dSH，以获得与所用关键点检测方法相同的关键点数量。

图10给出了不同方法的关键点检测示例。如预期的那样，我们观察到在振幅图像上应用LoG方法检测到的关键点主要在高反射率区域被检测到，而在高均匀性区域则发生了许多错误的检测。关于在图像对数上使用LoG方法检测到的关键点，在同质区域也发现了很多错误的检测结果，但它们都发生在高反射率区域和低反射率区域。但是，使用SAR-Harris方法检测到的关键点大多位于拐角和亮点上，并且在均匀区域上进行错误检测的次数确实很少。

2)方向分配和描述符提取：在原始的SIFT算法中，方向分配和描述符提取的步骤都依赖于梯度方向的直方图。这些直方图是在每个关键点的邻域上计算的，并由梯度幅度加权。

在这里，我们建议使用在第III-A节中介绍的按比例梯度(GR)方法计算这些直方图。而不是像原始SIFT描述符中那样使用正方形邻域和4×4正方形扇区，我们依赖于圆形邻域(大小为6σ)和对数极性扇区(如[28]中所示)，请参见图11。结果描述符称为比率描述符。让我们观察到，用于计算梯度的GR方法可以直接适用于扇区的其他空间配置，例如原始SIFT之一。

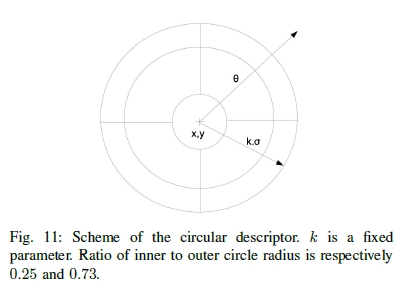
图11：循环描述符的方案。 k是固定参数。 内外半径之比分别为0.25和0.73。

为了选择主要方向，我们采用了一种相反的方法[28]。每个点最多选择两个方向。

IV 散斑噪声下SAR-SIFT算法的实验验证

在本节中，将提出的关键点和描述符与原始SIFT算法进行比较。我们首先通过测量关键点检测方法的重复率来研究其稳定性和鲁棒性。然后借助ROC曲线评估关键点检测方法和描述符的性能。为了仅评估算法处理斑点噪声的能力，对在相同条件下获取的图像对进行了研究。

A.测试图像和参数

对于这些实验，我们使用18对带有亚像素配准的TerraSAR-X图像提取物，代表法国图卢兹市。所有图像的尺寸均为512×512像素，并且都是在相同的观看条件(34°入射角，2m分辨率，SpotLight模式)下采集的。目视检查表明，每对两幅图像之间没有时间变化，因此仅噪声实现有所不同。

SIFT关键点通过LoG方法(LoG中的局部极值和多尺度Harris准则的阈值)进行检测。要构建刻度空间，我们选择以下参数：第一个刻度σ₀= 0.63，两个刻度之间的比率r = 2^1/3，刻度数量l_max = 13。对于多尺度哈里斯准则，参数t设置为0.04。对于8位图像，此标准dH的阈值通常设置为2000，但由于每个SAR图像具有不同的动态特性，因此将适用于每个SAR图像。

对于SAR-Harris方法，选择的参数为：β₀= 2第一个刻度，c = 2^1/3两个刻度之间的比率，m_max = 8刻度数，d = 0.04 SAR-Harris标准的任意参数。在对SAR-Harris准则在角，边界和同质区域上计算出的概率分布进行实验研究之后，阈值d_SH已设置为0.8。

对于比率和SIFT描述符，均在12个bin上计算直方图，并使用k = 12的对数极坐标网格。

B.关键点可重复性

重复性标准[36]给出了关于图像变化的关键点检测稳定性的度量。给定一对配准图像，对于第一张图像的每个关键点，我们用相同的方法在另一张图像上寻找最接近的一个。然后，对于不同的阈值u，可以观察到在另一幅图像上重复的关键点在小于u的距离处所占的百分比。

将第III-B1节中介绍的新的SAR-Harris关键点检测方法与应用于振幅图像和对数图像的LoG方法进行了比较。结果如图12所示。阈值dH已被调整为平均获得与SAR-Harris方法相同数量的关键点。对于整个集合，我们总共获得了使用原始LoG方法提取的25032个关键点，使用图像对数时的24729个关键点以及使用SAR-Harris方法提取的21253个关键点。因此，每种检测方法的关键点密度都相同。

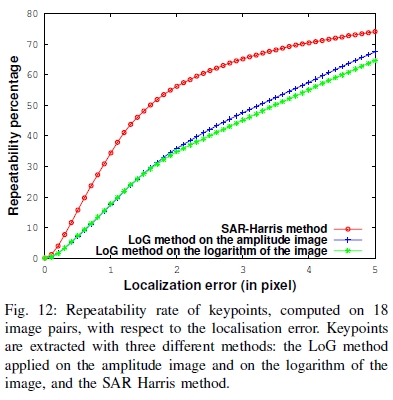
图12：相对于定位误差，在18个图像对上计算出的关键点的重复率。 通过三种不同方法提取关键点：应用于振幅图像和图像对数的LoG方法，以及SAR Harris方法。

可以看出，SAR-Harris方法的性能优于两种LoG方法。例如，在d = 1.5像素的定位误差下，将重复使用SAR-Harris方法提取的50％以上的关键点。对于使用其他两种方法提取的关键点，此比率仅为30％。我们还观察到，当将LoG方法应用于对数图像而不是幅度幅值时，其性能并未表现出改善。

C.比赛表现

针对关键点检测方法和描述符类型的不同组合计算全局ROC曲线。关键点与NNDR方法匹配(NN步骤然后是DR步骤，请参阅第II-A4节)。

令M_k(P_1,i，P_2,j)是图像I1的点P_1,i(x_1,i，y_1,i，σ_1,i，θ_1,i)与图像I2的点P_2,j(x_2,j，y_2,j，σ_2,j，θ_2,j)。考虑到图像I1与图像I2相比的变形T，如果满足以下条件，则将M_k定义为正确的：

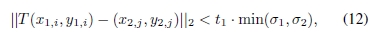
其中t₁设置为5。这里的图像对表示一个子像素配准，因此T是标识函数。

数量#CM_all和#FM_all分别定义为使用NN步骤对整个集合进行正确和错误匹配的总数。针对到最接近和第二最接近匹配的距离之比的阈值th的某个值，评估正确匹配和错误匹配的数量(分别为#CM和#FM)(DR步长)。为了获得接收器工作特性(ROC)曲线，通过改变th值，将正确匹配的关键点#CM /(＃CM_all +＃FM_all)的百分比相对于误报警率#FM /(＃CM +＃FM)进行绘制。

我们在这里比较了两个关键点检测方法，即幅值图像上的LoG方法和新的SAR-Harris方法，以及两个描述符，即建议的比率和常用的SIFT描述符。四种考虑情况的结果显示在图13中。由于图像没有旋转，因此没有为该实验的关键点分配方向，无论是SIFT还是SAR-SIFT方法都没有。测试L¹和L²距离以在匹配步骤计算描述符之间的相似度。我们已经观察到，L¹距离的结果总是比欧几里得距离更好。为了简化读取，仅显示L¹距离的匹配项。

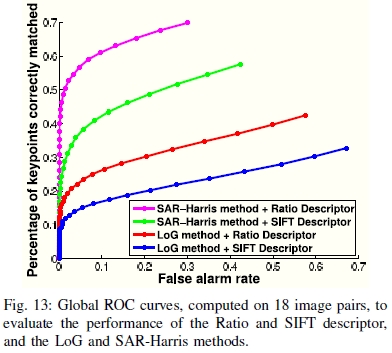
图13：在18个图像对上计算的全局ROC曲线，用于评估Ratio和SIFT描述子以及LoG和SAR-Harris方法的性能。

我们观察到，SAR-Harris关键点检测方法和比率描述符的结合可以实现最佳性能。实际上，对于1％的错误警报率，几乎可以获得50％的正确匹配，而对于其他配置，该比率小于30％。1％错误警报率是在具有一定th值的对应关系中而不是在所有可能的匹配中错误匹配的百分比。同样，将SAR-Harris方法与SIFT描述符结合使用已经大大改善了算法的性能。相反，将LoG方法与比率描述符一起使用提供的功能有限。

总而言之，SAR-Harris方法比LoG方法更稳定，对噪声更鲁棒。比率描述符的性能优于SIFT描述符。 SAR-SIFT算法中使用了SAR-Harris和比率描述符的组合(图8)。因此，该算法比SAR图像上的原始SIFT算法可获得更好的结果。

Ⅴ SAR-SIFT算法在更多复杂情况和应用中的实验验证

在通过实验验证SAR-SIFT算法处理强SAR噪声的效率之后，我们分析了它在更复杂的情况下(尤其是在不同的采集模式下)的行为。然后建议使用RANSAC算法来增加正确匹配的次数，同时对于存在整体变形的某些特定情况，保持较低的误报率。
最后，考虑了SAR-SIFT算法的两个应用，即配准和变化检测。

A. SAR-SIFT在不同图像观看条件下的行为

现在，我们将研究重点放在具有不同分辨率和/或不同入射角的图像对上。为了提供参考情况，我们还考虑具有相同观看条件的图像对。对于只有分辨率差异的情况，我们可以期待一些好的结果。当入射角改变时，情况更加复杂，因为图像几何形状和SAR信号不同。因此，可以预料，在这种情况下，关联关键点的数量将减少。本节研究此数字在不同条件下的可变性。

可用的图像集及其特征(传感器，入射角，分辨率，模式)，图像数量和以像素为单位的大小如表I所示。

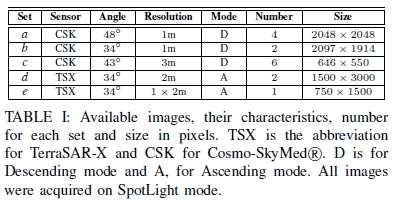
表I：可用图像，它们的特征，每组的数量和以像素为单位的大小。 TSX是Cosmo-SkyMed R的TerraSAR-X和CSK的缩写。 D代表降序模式，A代表升序模式。 所有图像都是在SpotLight模式下获取的。

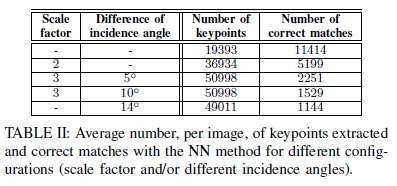
表II：针对不同配置(比例因子和/或不同入射角)，每个图像提取的关键点的平均数量，并使用NN方法进行正确匹配。

对于具有相同观看条件的图像，在集合a，b和c的每个图像之间计算匹配。为了获得具有变化的分辨率的情况，已经针对集合d的图像在方位角方向上计算了多视，以获得关于集合e的图像的比例因子为2。对于入射角不同的情况，集合a和b用于研究入射角为14°的情况。两者也都与集合c进行了比较，但是在那些情况下，分辨率也有所不同。因此考虑了五种配置。

已在所有考虑的图像之间手动估算了地面真实变形网格1。参数t₁设置为5，入射角不同的情况除外，该参数设置为7。实际上，由于倾斜范围变形，在这些情况下建筑物的大小可能会有所不同，应考虑使用更宽松的阈值。在此，SARSIFT和SIFT算法均通过方向分配执行。

我们首先观察到算法仅使用NN步骤来匹配相应关键点的能力(第II-A4节)。我们要验证该算法可以获取足够数量的正确匹配，而无需考虑“距离比率”步骤。表II列出了每种配置在没有阈值的情况下提取的关键点的平均数量和每个图像的正确匹配。

接下来，改变DR阈值(允许拒绝错误对应)以生成ROC曲线。使用与IV-C节相同的符号，针对不同的th值，将正确匹配#CM / #CM_all的百分比与错误匹配#FM /(＃CM +＃FM)的百分比作图，见图14。

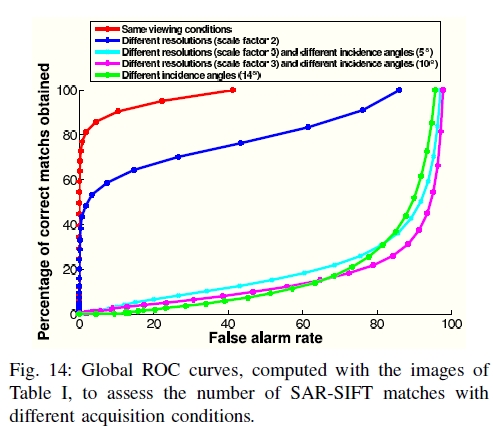
图14：用表I的图像计算的全局ROC曲线，以评估不同采集条件下SAR-SIFT匹配的次数。

可以预料，具有相同观看条件或分辨率差异的情况会给出非常好的分数。 NN步骤允许正确匹配高比例的关键点，分别为59％和14％。在这些正确的匹配项中，使用DR步骤可以仅分别得到大约80％和45％的误报率。

但是，考虑入射角差时，得分确实很低。 NN步骤只能匹配少量的关键点(介于2％和4％之间)。由于提取的关键点数量足够大，因此仍然可以正确匹配大量关键点。但是，匹配的DR部分不足以过滤错误的对应，并且很难以低的误报率获得足够数量的正确匹配。有趣的是，与入射角不同，分辨率差异的影响非常有限。确实，集合a和b之间的匹配具有14°的入射角差和相同的分辨率，显示的分数比集合b和c与a和c之间的匹配弱，两者的比例因子均为3，且入射角差分别为9°和5°。

在具有相同观看条件或仅具有分辨率差异的图像上，图像几何​​形状几乎不变，SARSIFT可以实现大量正确的关键点匹配(始终超过一千)。但是，在入射角不同的情况下，SAR信号会发生变化，并且SAR-SIFT的不变性不会考虑相应的失真。差异越大，图像变化就越大，SAR-SIFT很难找到对应的关键点。

B.筛选错误匹配以搜索整体变形：AC-RANSAC

1)提议的方法：如前一段所述，关键点匹配的过滤部分(DR步骤)在入射角不同的情况下会失败。

然而，出于配准的目的和作为第一近似，卫星图像对可以通过整体变形来关联。在多视图环境和大致平坦的场景中，这种变形通常通过仿射变换来建模[37]。当以不同的入射角获取时，SAR图像确实表现出局部位移。但是，两个SAR图像之间的全局关系可以用此模型来描述，只要它们是由相同的传感器以相同的模式采集的。

该先验信息可以有助于抑制配准申请中的错误对应。我们建议使用RANSAC算法[38]以获得大量的正确匹配项，并且误报率较低。该算法可用于估计异常值(错误对应)存在时的整体变形，从而提供一组连贯的对应。我们选择使用反向交流的RANSAC版本，称为AC-RANSAC [39]，即使异常值百分比很高(高达90％)，也能产生良好的结果。它还具有仅需要一个参数即迭代次数imax的优点。

2)实验结果：AC-RANSAC已应用于表II中第五种情况的图像对应关系，呈现最大的入射角差。为了获得正确匹配的最大数量，不应用DR过滤部分。我们仅使用NN步骤将所有结果对应关系称为简单匹配。但是，为了加快处理速度，在距离之间的比率小于阈值th = 0.9的情况下，随机选择用于估计变形的匹配项。我们选择i_max = 10000作为迭代次数，并选择仿射变换作为全局变形。在表III中，在应用AC-RANSAC之前和之后，每幅图像的虚假和真实对应的平均数量在表III中给出。

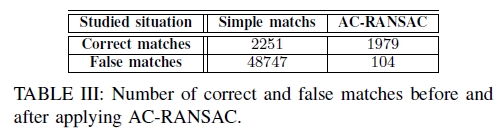
表III：应用AC-RANSAC之前和之后正确和错误匹配的次数。

使用AC-RANSAC可以抑制几乎所有错误匹配，同时保留88％的正确匹配。离群值的百分比从约95％增至5％。我们可以通过合理百分比的错误警报来实现大量正确的匹配。

C. SAR-SIFT在配准中的应用

如第V-B节所述，可以通过仿射变换来近似估计在同一传感器下以相同模式采集的两个图像之间的变形。但是，此近似值仅对地面上的点有效。AC-RANSAC已经证明可以有效地过滤大量错误匹配以进行配准，还可以用于估计两个图像之间的仿射变换。我们在此提出在入射角变化的情况下SAR-SIFT算法的配准应用。

1)建议的方法：要配准此类图像，我们需要估计以下多项式变换的系数：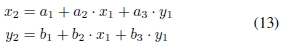

可以使用两个图像之间的关键点匹配来完成系数的最小二乘估计。但是，如第V-A节所示，在这些情况下，该算法的效率较低，因此我们面临着大量异常值的风险。如第V-B节所述，AC-RANSAC算法可以帮助在存在异常值的情况下对变形进行建模，并且可以有效地过滤错误的对应关系。

为了估计等式(13)的参数，我们建议将该算法应用于SAR-Harris算法在两个SAR图像之间获得的匹配。使用第V-B节中介绍的相同过程和参数值。这种配准方法将进一步称为SAR-SIFT + AC-RANSAC。

2)评估：表IV描述了用于评估套准精度的图像对。它们具有相同的分辨率，但入射角相差14°。由于没有可用的地面真相，我们在这副图像上手动提取了30个地面控制点(GCP)。然后将这些用于实现手动配准以及配准精度的度量。

表IV：用于评估SAR-Harris + AC-RANSAC执行的配准精度的图像对。 图像在法国图卢兹地区获取。

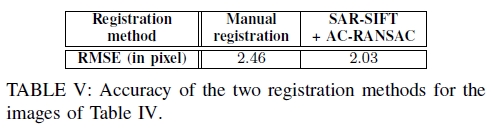
表V：表IV图像的两种配准方法的准确性。

随机选择十个GCP以评估等式(13)的参数并获得手动配准。其他二十个点用于测量两种配准方法的准确性，一种通过使用SAR-SIFT + AC-RANSAC，另一种是先前的手册，通过计算均方根误差(RMSE)来进行。重复此过程10000次，表V中列出了平均RMSE。SAR-SIFT + AC-RANSAC方法叠加了两个配准图像，如图15所示。

图15：用SAR-SIFT + ACRANSAC方法叠加表IV的两个配准图像(角度差14°)。 主映像为红色，从属映像为蓝色。

自动方法SAR-SIFT + AC-RANSAC与手动方法相比具有良好的套准精度。考虑到提取GCP非常耗时且容易出错，因此这种新方法是一种有趣的自动配准SAR图像的有趣方法，可用于不同类型的采集。

D.变更检测应用程序：初步结果

SAR-SIFT的另一种可能的应用是变化检测。此类应用程序经常会出现配准错误，基于特征的方法的使用可以避免预配准步骤。

图16：来自法国图卢兹地区的具有34°入射角和2m分辨率的TerraSAR-X图像摘录。

作为初步结果，我们对呈现出一些变化的图像对进行了匹配(图16)。一幅图像于2007年获得，另一幅图像于2008年获得，见图16。然后使用AC-RANSAC算法过滤获得的对应关系。在发生变化的区域中，我们假设检测到关键点但不匹配。为了检验该假设，进行了以下实验：从而取消了距离匹配项小于40像素的每个关键点。图17中显示了2007年映像中的其余关键点。

图17：显示2007年图像时，所有关键点与2007年图像和2008年图像之间的匹配距离至少40个像素。

我们观察到，剩余的点在两个主要站点上都发生了变化，并且发生了一些错误。未检测到较小的变化，但是所使用的算法非常简单，并且40个像素的容限阈值很高。

从这个初步的实验中，我们认为可以将SARSIFT算法用于变化检测应用。应该开发更复杂的算法，例如使用关键点密度。

VI 结论

本文介绍了一种适用于SAR图像的类似于SIFT的新描述符。它依赖于适用于SAR图像且对斑点噪声具有鲁棒性的新梯度计算。然后使用这种新的梯度计算方法，即“按比例梯度(GRient)”，以改进SIFT算法的步骤。一种新的基于多尺度哈里斯探测器的关键点检测方法可提供稳定的关键点。与原始SIFT相比，GR提供的稳健的梯度方向能够为SAR图像获得更有效的描述符。

通过应用反向搜索RANSAC，可以实现一致数量的正确匹配，从而允许将这种类似于SIFT的新算法用于各种应用。在本文中，提出了一种有效的SAR图像配准应用程序，用于困难的情况，例如入射角变化。诸如更改检测或对象匹配之类的其他应用程序将成为进一步工作的主题。

Ⅶ 致谢

作者要感谢CNES和ASI航天局提供的Cosmo-Skymed R图像，感谢德国航空航天中心提供的TerraSAR-X图像R DLR 2007-2008的摘录。他们还要感谢Jean-Marie Nicolas对传感器参数配准的帮助，以及Baptiste Mazin对SIFT算法提供的源代码的帮助。

参考文献

[1] D. G. Lowe, “Distinctive image features from scale-invariant keypoints,” Int. J. Comput. Vision, vol. 60, pp. 91–110, 2004.
[2] K. Mikolajczyk and C. Schmid, “A performance evaluation of local descriptors,” Pattern Analysis and Machine Intelligence, IEEE Transactions on, vol. 27, no. 10, pp. 1615–1630, oct. 2005.
[3] Qiaoliang Li, Guoyou Wang, Jianguo Liu, and Shaobo Chen, “Robust scale-invariant feature matching for remote sensing image registration,” Geoscience and Remote Sensing Letters, IEEE, vol. 6, no. 2, pp. 287– 291, April.
[4] Chunlei Huo, Chunhong Pan, Leigang Huo, and Zhixin Zhou, “Multilevel SIFT matching for large-size VHR image registration,” Geoscience and Remote Sensing Letters, IEEE, vol. 9, no. 2, pp. 171–175, 2012.
[5] A. Sedaghat, M. Mokhtarzade, and H. Ebadi, “Uniform robust scaleinvariant feature matching for optical remote sensing images,” Geoscience and Remote Sensing, IEEE Transactions on, vol. 49, no. 11, pp.4516–4527, 2011.
[6] Yi Yang and S. Newsam, “Geographic image retrieval using local invariant features,” Geoscience and Remote Sensing, IEEE Transactions on, vol. 51, no. 2, pp. 818–832, 2013.
[7] V. Risojevic and Z. Babic, “Fusion of global and local descriptors for remote sensing image classification,” Geoscience and Remote Sensing Letters, IEEE, vol. 10, no. 4, pp. 836–840, 2013.
[8] B. Sirmacek and C. Unsalan, “Urban-area and building detection using SIFT keypoints and graph theory,” Geoscience and Remote Sensing, IEEE Transactions on, vol. 47, no. 4, pp. 1156–1167, 2009.
[9] Chao Tao, Yihua Tan, Huajie Cai, and Jinwen Tian, “Airport detection from large IKONOS images using clustered SIFT keypoints and region information,” Geoscience and Remote Sensing Letters, IEEE, vol. 8, no.1, pp. 128–132, 2011.
[10] J.Z. Liu and X.C. Yu, “Research on SAR image matching technology based on SIFT,” in ISPRS08, 2008, p. B1: 403 ff.
[11] Sahil Suri, Peter Schwind, Peter Reinartz, and Johannes Uhl, “Combining mutual information and scale invariant feature transform for fast and robust multisensor SAR image registration,” in 75th Annual ASPRS Conference, 2009.
[12] P. Schwind, S. Suri, P. Reinartz, and A. Siebert, “Applicability of the SIFT operator to geometric SAR image registration,” Int. J. Remote Sens., vol. 31, no. 8, pp. 1959–1980, Mar. 2010.
[13] Sahil Suri, Peter Schwind, Johannes Uhl, and Peter Reinartz, “Modifications in the SIFT operator for effective SAR image matching,” International Journal of Image and Data Fusion, vol. 1, no. 3, pp. 243– 256, 2010.
[14] J. Lu, B. Wang, H. M. Gao, and Z.Q. Zhou, “SAR images matching based on local shape descriptors,” in Radar Conference, 2009 IET International, 2009, pp. 1–4.
[15] Lining Liu, Yunhong Wang, and Yiding Wang, “SIFT based automatic tie-point extraction for multitemporal SAR images,” in Education Technology and Training, 2008. and 2008 International Workshop on Geoscience and Remote Sensing. ETT and GRS 2008. International Workshop on, 2008, vol. 1, pp. 499–503.
[16] Wentao Lv, Wenxian Yu, Junfeng Wang, and Kaizhi Wang, “SAR image matching based on SIFT keypoints and multi-subregions information,” in Synthetic Aperture Radar (APSAR), 2011 3rd International Asia-Pacific Conference on, 2011, pp. 1–4.
[17] Bin Fan, Chunlei Huo, Chunhong Pan, and Qingqun Kong, “Registration of optical and SAR satellite images by exploring the spatial relationship of the improved SIFT,” Geoscience and Remote Sensing Letters, IEEE, vol. 10, no. 4, pp. 657 –661, july 2013.
[18] B. Wessel, M. Huber, and A. Roth, “Registration of near real-time SAR images by image-to-image matching,” in PIA07, 2007, p. 179.
[19] Yu Xiaoping, Liu Tong, Li Pingxiang, and Huang Guoman, “The application of improved SIFT algorithm in high resolution SAR image matching in mountain areas,” in Image and Data Fusion (ISIDF), 2011 International Symposium on, 2011, pp. 1–4.
[20] F. Dellinger, J. Delon, Y. Gousseau, J. Michel, and F. Tupin, “SAR-SIFT: A SIFT-like algorithm for applications on SAR images,” in Geoscience and Remote Sensing Symposium (IGARSS), 2012 IEEE International, 2012, pp. 3478–3481.
[21] Tony Lindeberg, “Feature detection with automatic scale selection,” International Journal of Computer Vision, vol. 30, pp. 79–116, 1998.
[22] Yves Dufournaud, Cordelia Schmid, and Radu P. Horaud, “Matching images with different resolutions,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head Island, South Carolina, USA. 2000, pp. 612–618, IEEE Computer Society Press.
[23] K. Mikolajczyk and C. Schmid, “Indexing based on scale invariant interest points,” in Computer Vision, 2001. ICCV 2001. Proceedings.Eighth IEEE International Conference on, 2001, vol. 1, pp. 525–531 vol.1.
[24] Krystian Mikolajczyk and Cordelia Schmid, “Scale and affine invariant interest point detectors,” International Journal of Computer Vision, vol.60, no. 1, pp. 63–86, 2004.
[25] K. Mikolajczyk and C. Schmid, “An affine invariant interest point detector,” in Proceedings of the 7th European Conference on Computer Vision-Part I, London, UK, UK, 2002, ECCV ’02, pp. 128–142, Springer-Verlag.
[26] Jean-Michel Morel and Guoshen Yu, “ASIFT: A new framework for fully affine invariant image comparison,” SIAM J. Img. Sci., vol. 2, no.2, pp. 438–469, Apr. 2009.
[27] Herbert Bay, Tinne Tuytelaars, and Luc Van Gool, “SURF: Speeded up robust features,” in In ECCV, 2006, pp. 404–417.
[28] J. Rabin, J. Delon, and Y. Gousseau, “A statistical approach to the matching of local features,” SIAM J. Img. Sci., vol. 2, pp. 931–958, September 2009.
[29] Yan Ke and R. Sukthankar, “PCA-SIFT: a more distinctive representation for local image descriptors,” in Computer Vision and Pattern Recognition, 2004. CVPR 2004. Proceedings of the 2004 IEEE Computer Society Conference on, 2004, vol. 2, pp. II–506–II–513 Vol.2.
[30] Shanhu Wang, Hongjian You, and Kun Fu, “BFSIFT: A novel method to find feature matches for SAR image registration,” Geoscience and Remote Sensing Letters, IEEE, vol. 9, no. 4, pp. 649 –653, july 2012.
[31] Yingdan Wu and Ming Yang, “A multi-sensor remote sensing image matching method based on SIFT operator and CRA similarity measure,” in Intelligence Science and Information Engineering (ISIE), 2011 International Conference on, 2011, pp. 115–118.
[32] R. Touzi, A. Lopes, and P. Bousquet, “A statistical and geometrical edge detector for SAR images,” Geoscience and Remote Sensing, IEEE Transactions on, vol. 26, no. 6, pp. 764–773, nov 1988.
[33] A.C. Bovik, “On detecting edges in speckle imagery,” Acoustics, Speech and Signal Processing, IEEE Transactions on, vol. 36, no. 10, pp. 1618 –1627, oct 1988.
[34] C.J. Oliver, D. Blacknell, and R.G. White, “Optimum edge detection in SAR,” Radar, Sonar and Navigation, IEE Proceedings -, vol. 143, no.1, pp. 31 –40, feb 1996.
[35] R. Fjortoft, A. Lopes, P. Marthon, and E. Cubero-Castan, “An optimal multiedge detector for SAR image segmentation,” Geoscience and Remote Sensing, IEEE Transactions on, vol. 36, no. 3, pp. 793–802, may 1998.
[36] Cordelia Schmid, Roger Mohr, and Christian Bauckhage, “Evaluation of interest point detectors,” Int. J. Comput. Vision, vol. 37, no. 2, pp.151–172, June 2000.
[37] Barbara Zitov and Jan Flusser, “Image registration methods: a survey,” Image and Vision Computing, vol. 21, pp. 977–1000, 2003.
[38] Martin A. Fischler and Robert C. Bolles, “Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography,” Commun. ACM, vol. 24, no. 6, pp. 381–395, June 1981.
[39] Julien Rabin, Julie Delon, Yann Gousseau, and Lionel Moisan, “MACRANSAC: a robust algorithm for the recognition of multiple objects,” in Proceedings of 3DPTV 2010, Paris, France, 2010, p. 051.