MCMC(一)蒙特卡罗方法

　　　　MCMC(一)蒙特卡罗方法

　　　　MCMC(二)马尔科夫链（待填坑）

　　　　MCMC(三)M-H采样和Gibbs采样（待填坑）

　　　　作为一种随机采样方法，马尔科夫链蒙特卡罗（Markov Chain Monte Carlo，以下简称MCMC）在机器学习,深度学习以及自然语言处理等领域都有广泛的应用，是很多复杂算法求解的基础。比如我们前面讲到的分解机(Factorization Machines)推荐算法，还有前面讲到的受限玻尔兹曼机（RBM）原理总结，都用到了MCMC来做一些复杂运算的近似求解。下面我们就对MCMC的原理做一个总结。

1. MCMC概述

　　　　从名字我们可以看出，MCMC由两个MC组成，即蒙特卡罗方法（Monte Carlo Simulation，简称MC）和马尔科夫链（Markov Chain ，也简称MC）。要弄懂MCMC的原理我们首先得搞清楚蒙特卡罗方法和马尔科夫链的原理。我们将用三篇来完整学习MCMC。在本篇，我们关注于蒙特卡罗方法。

2. 蒙特卡罗方法引入

　　　　蒙特卡罗原来是一个赌场的名称，用它作为名字大概是因为蒙特卡罗方法是一种随机模拟的方法，这很像赌博场里面的扔骰子的过程。最早的蒙特卡罗方法都是为了求解一些不太好求解的求和或者积分问题。比如积分：$$\theta = \int_a^b f(x)dx$$

　　　　如果我们很难求解出$f(x)$的原函数，那么这个积分比较难求解。当然我们可以通过蒙特卡罗方法来模拟求解近似值。如何模拟呢？假设我们函数图像如下图:

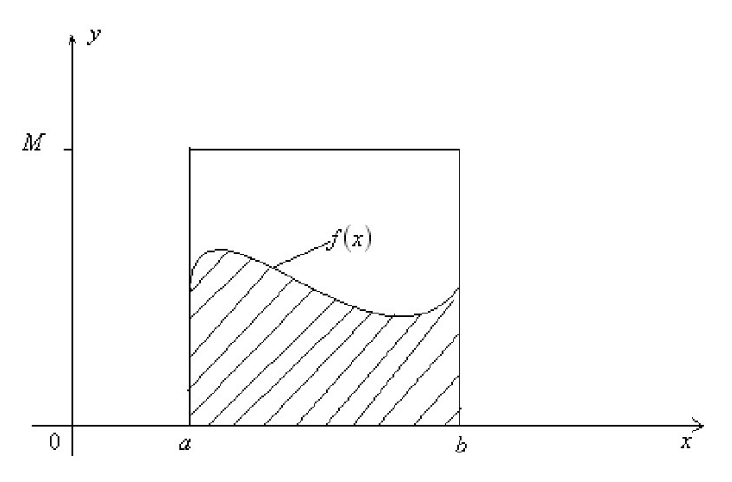
　　　　则一个简单的近似求解方法是在[a,b]之间随机的采样一个点。比如$x_0$,然后用$f(x_0)$代表在[a,b]区间上所有的$f(x)$的值。那么上面的定积分的近似求解为:$$(b-a)f(x_0)$$

　　　　当然，用一个值代表[a,b]区间上所有的$f(x)$的值，这个假设太粗糙。那么我们可以采样[a,b]区间的n个值：${x_0,x_1,...x_{n-1}}$,用它们的均值来代表[a,b]区间上所有的$f(x)$的值。这样我们上面的定积分的近似求解为:$$\frac{b-a}{n}\sum\limits_{i=0}^{n-1}f(x_i)$$

　　　　虽然上面的方法可以一定程度上求解出近似的解，但是它隐含了一个假定，即$x$在[a,b]之间是均匀分布的，而绝大部分情况，$x$在[a,b]之间不是均匀分布的。如果我们用上面的方法，则模拟求出的结果很可能和真实值相差甚远。　

　　　　怎么解决这个问题呢？ 如果我们可以得到$x$在[a,b]的概率分布函数$p(x)$，那么我们的定积分求和可以这样进行：$$\theta = \int_a^b f(x)dx =  \int_a^b \frac{f(x)}{p(x)}p(x)dx \approx \frac{1}{n}\sum\limits_{i=0}^{n-1}\frac{f(x_i)}{p(x_i)}$$

　　　　上式最右边的这个形式就是蒙特卡罗方法的一般形式。当然这里是连续函数形式的蒙特卡罗方法，但是在离散时一样成立。

　　　　可以看出，最上面我们假设$x$在[a,b]之间是均匀分布的时候，$p(x_i) = 1/(b-a)$，带入我们有概率分布的蒙特卡罗积分的上式，可以得到：$$\frac{1}{n}\sum\limits_{i=0}^{n-1}\frac{f(x_i)}{1/(b-a)} = \frac{b-a}{n}\sum\limits_{i=0}^{n-1}f(x_i) $$

　　　　也就是说，我们最上面的均匀分布也可以作为一般概率分布函数$p(x)$在均匀分布时候的特例。那么我们现在的问题转到了如何求出$x$的分布$p(x)$上。

3. 概率分布采样

　　　　上一节我们讲到蒙特卡罗方法的关键是得到$x$的概率分布。如果求出了$x$的概率分布，我们可以基于概率分布去采样基于这个概率分布的n个$x$的样本集，带入蒙特卡罗求和的式子即可求解。　

　　　　但是还有一个关键的问题需要解决，即如何基于概率分布去采样基于这个概率分布的n个$x$的样本集。　

　　　　对于常见的均匀分布$uniform(0,1)$是非常容易采样样本的，一般通过线性同余发生器可以很方便的生成(0,1)之间的伪随机数样本。而其他常见的概率分布，无论是离散的分布还是连续的分布，它们的样本都可以通过$uniform(0,1)$的样本转换而得。比如二维正态分布的样本$(Z_1,Z_2)$可以通过通过独立采样得到的$uniform(0,1)$样本对$(X_1,X_2)$通过如下的式子转换而得：$$Z_1 = \sqrt{-2 ln X_1}cos(2\pi X_2)$$$$Z_2 = \sqrt{-2 ln X_1}sin(2\pi X_2)$$

　　　　其他一些常见的连续分布，比如t分布，F分布，Beta分布，Gamma分布等，都可以通过类似的方式从$uniform(0,1)$得到的采样样本转化得到。在python的numpy，scikit-learn等类库中，都有生成这些常用分布样本的函数可以使用。

　　　　不过很多时候，我们的$x$的概率分布不是常见的分布，这意味着我们没法方便的得到这些非常见的概率分布的样本集。那这个问题怎么解决呢？

4. 接受-拒绝采样

　　　　对于概率分布不是常见的分布，一个可行的办法是采用接受-拒绝采样来得到该分布的样本。既然 $p(x)$ 太复杂在程序中没法直接采样，那么我设定一个程序可抽样的分布 $q(x)$ 比如高斯分布，然后按照一定的方法拒绝某些样本，以达到接近 $p(x)$ 分布的目的，其中$q(x)$叫做 proposal distribution。

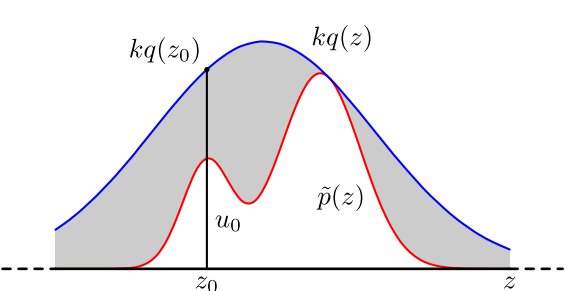
　　　　具体采用过程如下，设定一个方便采样的常用概率分布函数 $q(x)$，以及一个常量 $k$，使得 $p(x)$ 总在 $kq(x)$ 的下方。如上图。

　　　　首先，采样得到$q(x)$的一个样本$z_0$，采样方法如第三节。然后，从均匀分布$（0, kq(z_0)) $中采样得到一个值$u$。如果$u$落在了上图中的灰色区域，则拒绝这次抽样，否则接受这个样本$z_0$。重复以上过程得到n个接受的样本$z_0,z_1,...z_{n-1}$,则最后的蒙特卡罗方法求解结果为：$$\frac{1}{n}\sum\limits_{i=0}^{n-1}\frac{f(z_i)}{p(z_i)}$$

　　　　整个过程中，我们通过一系列的接受拒绝决策来达到用$q(x)$模拟$p(x)$概率分布的目的。

5. 蒙特卡罗方法小结

　　　　使用接受-拒绝采样，我们可以解决一些概率分布不是常见的分布的时候，得到其采样集并用蒙特卡罗方法求和的目的。但是接受-拒绝采样也只能部分满足我们的需求，在很多时候我们还是很难得到我们的概率分布的样本集。比如：

　　　　1）对于一些二维分布$p(x,y)$，有时候我们只能得到条件分布$p(x|y)$和$p(y|x)$和,却很难得到二维分布$p(x,y)$一般形式，这时我们无法用接受-拒绝采样得到其样本集。

　　　　2）对于一些高维的复杂非常见分布$p(x1,x2,...,x_n)，我们要找到一个合适的$q(x)$和$k$非常困难。

　　　　从上面可以看出，要想将蒙特卡罗方法作为一个通用的采样模拟求和的方法，必须解决如何方便得到各种复杂概率分布的对应的采样样本集的问题。而我们下一篇要讲到的马尔科夫链就是帮助找到这些复杂概率分布的对应的采样样本集的白衣骑士。下一篇我们来总结马尔科夫链的原理。

（欢迎转载，转载请注明出处。欢迎沟通交流： pinard.liu@ericsson.com）