NLP —— 图模型（零）：EM算法简述及简单示例（三硬币模型）

最近接触了pLSA模型，该模型需要使用期望最大化（Expectation Maximization）算法求解。

本文简述了以下内容：

为什么需要EM算法

EM算法的推导与流程

EM算法的收敛性定理

使用EM算法求解三硬币模型

为什么需要EM算法

数理统计的基本问题就是根据样本所提供的信息，对总体的分布或者分布的数字特征作出统计推断。所谓总体，就是一个具有确定分布的随机变量，来自总体的每一个iid样本都是一个与总体有相同分布的随机变量。

参数估计是指这样一类问题——总体所服从的分布类型已知，但某些参数未知：设 $Y_1,...,Y_N$ 是来自总体 $\textbf Y$ 的iid样本，记 $Y=(y_1,...,y_N)$ 是样本观测值，如果随机变量 $Y_1,...,Y_N$ 是可观测的，那么直接用极大似然估计法就可以估计参数 $\theta$ 。

但是，如果里面含有不可观测的隐变量，使用MLE就没那么容易。EM算法正是服务于求解带有隐变量的参数估计问题。

EM算法的推导与流程

下面考虑带有隐变量 $\textbf Z$ (观测值为 $z$ )的参数估计问题。将观测数据（亦称不完全数据）记为 $Y=(y_1,...,y_N)$ ，不可观测数据记为 $Z=(z_1,...,z_N)$ ， $Y$ 、$Z$ 合在一起称为完全数据。那么观测数据的似然函数为$$l(\theta)=\prod_{j=1}^NP(y_j|\theta)=\prod_{j=1}^N\sum_zP(z|\theta)P(y_j|z,\theta)$$

其中求和号表示对 $z$ 的所有可能取值求和。

为了省事，表述成这个形式：$$l(\theta)=P(Y|\theta)=\sum_zP(z|\theta)P(Y|z,\theta)$$

对数似然：$$L(\theta)=\ln P(Y|\theta)=\ln \sum_zP(z|\theta)P(Y|z,\theta)$$

EM算法是一种迭代算法，通过迭代的方式求取目标函数 $L(\theta)=\ln P(Y|\theta)$ 的极大值。因此，希望每一步迭代之后的目标函数值会比上一步迭代结束之后的值大。设当前第 $n$ 次迭代后参数取值为 $\theta_n$ ，我们的目的是使 $L(\theta_{n+1})>L(\theta_n)$ 。那么考虑：

$$L(\theta)-L(\theta_n)=\ln (\sum_zP(z|\theta)P(Y|z,\theta))-\ln P(Y|\theta_n)$$

使用琴生不等式（Jensen inequality）：

$$\ln\sum_j\lambda_jy_j\geq \sum_j\lambda_j\log y_j,\quad \lambda_j\ge 0,\sum_j\lambda_j=1$$

因为 $\sum_zP(z|Y,\theta_n)=1$ ，所以 $L(\theta)-L(\theta_n)$ 的第一项有

$$\begin{aligned} \ln (\sum_zP(z|\theta)P(Y|z,\theta))&=\ln (\sum_zP(z|Y,\theta_n)\frac{P(z|\theta)P(Y|z,\theta)}{P(z|Y,\theta_n)})\\&\ge \sum_zP(z|Y,\theta_n)\ln \frac{P(z|\theta)P(Y|z,\theta)}{P(z|Y,\theta_n)}\end{aligned}$$

第二项有

$$ -\ln P(Y|\theta_n)=-\sum_zP(z|Y,\theta_n)\ln P(Y|\theta_n) $$

则 $L(\theta)-L(\theta_n)$ 的下界为

$$\begin{aligned} L(\theta)-L(\theta_n)&\ge\sum_zP(z|Y,\theta_n)\ln\frac{P(z|\theta)P(Y|z,\theta)}{P(z|Y,\theta_n)}-\sum_zP(z|Y,\theta_n)\ln P(Y|\theta_n)\\&=\sum_z[P(z|Y,\theta_n)\ln\frac{P(z|\theta)P(Y|z,\theta)}{P(z|Y,\theta_n)}-P(z|Y,\theta_n)\ln P(Y|\theta_n)]\\&=\sum_zP(z|Y,\theta_n)\ln\frac{P(z|\theta)P(Y|z,\theta)}{P(Y|\theta_n)P(z|Y,\theta_n)} \end{aligned}$$

定义一个函数 $l(\theta|\theta_n)$ ：

$$l(\theta|\theta_n)\triangleq L(\theta_n)+\sum_zP(z|Y,\theta_n)\ln\frac{P(z|\theta)P(Y|z,\theta)}{P(Y|\theta_n)P(z|Y,\theta_n)}$$

从而有 $L(\theta)\ge l(\theta|\theta_n)$ ，也就是说第 $n$ 次迭代结束后， $L(\theta)$ 的一个下界为 $l(\theta|\theta_n)$ 。另外，有等式 $L(\theta_n)=l(\theta_n|\theta_n)$ 成立。

我们的目的是使下一次迭代后得到的目标函数值能够大于当前的值： $L(\theta_{n+1})>L(\theta_n)$ ，即 $L(\theta_{n+1})>l(\theta_n|\theta_n)$ 。

而在当前， $L(\theta)$ 的下界为 $l(\theta|\theta_n)$ ，因此，任何能让 $l(\theta|\theta_n)$ 增大的 $\theta$ ，也可以让 $L(\theta)$ 增大。

      也就是说，能满足 $l(\theta_{n+1}|\theta_n)>l(\theta_n|\theta_n)$ 的 $\theta_{n+1}$ ，一定更能满足$L(\theta_{n+1})>l(\theta_n|\theta_n)=L(\theta_n)$ 。

      通过下图（来源：参考资料[1]，自己做了点注释）可以解释：

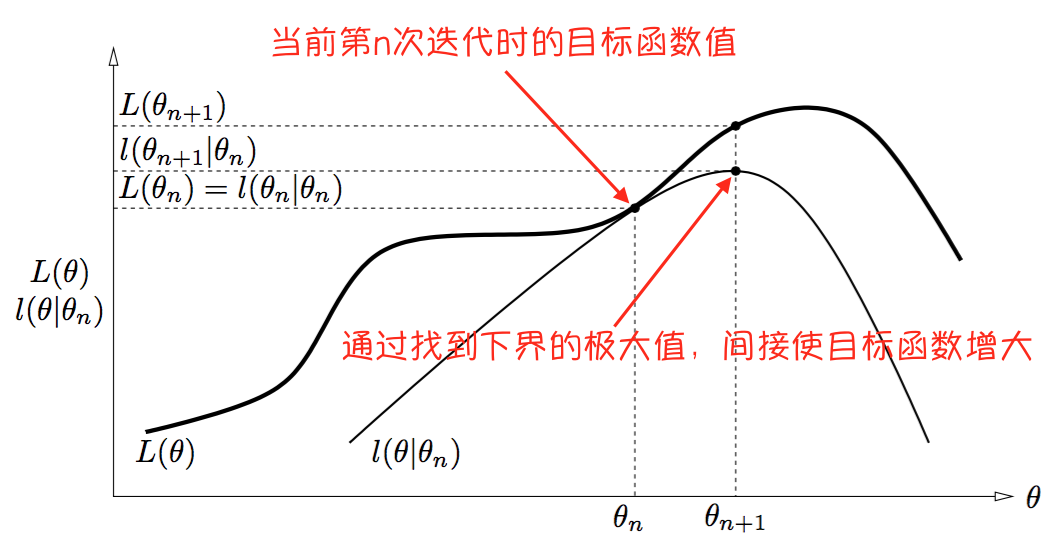
需要注意的是，下界的曲线当然是随着迭代的进行而变化的：在第 $i$ 次迭代结束后，总是有不等式 $L(\theta)\ge l(\theta|\theta_i)$ 和等式 $L(\theta_i)=l(\theta_i|\theta_i)$ 成立。

换句话说，EM算法通过优化对数似然在当前的下界，来间接优化对数似然。

ok，那么现在问题就从找满足 $L(\theta_{n+1})>L(\theta_n)$ 的 $\theta_{n+1}$ ，

转变成了找满足 $l(\theta_{n+1}|\theta_n)>l(\theta_n|\theta_n)$ 的 $\theta_{n+1}$ 。如何找到这样一个 $\theta_{n+1}$ ？直接找 $l(\theta|\theta_n)$ 的最优解呗：

$$\theta_{n+1}=\arg\max_\theta l(\theta|\theta_n)$$

把 $l(\theta|\theta_n)$ 中的几个与 $\theta$ 无关的量去掉，从而有

$$\begin{aligned} \theta_{n+1}&=\arg\max_\theta \sum_zP(z|Y,\theta_n)\ln [P(z|\theta)P(Y|z,\theta)]\\&=\arg\max_\theta \sum_zP(z|Y,\theta_n)\ln P(Y,z|\theta) \end{aligned}$$

回顾一下随机变量的期望的表达式：

$$\mathbb E[\textbf Z]=\sum_kP(\textbf Z=z_k)z_k$$

$$\mathbb E[g(\textbf Z)]=\sum_kP(\textbf Z=z_k)g(z_k)$$

$$\mathbb E[\textbf Z|\textbf Y=y]=\sum_kP(\textbf Z=z_k|\textbf Y=y)z_k$$

所以：

$$\begin{aligned} \theta_{n+1}&=\arg\max_\theta \mathbb E_{\textbf Z|\textbf Y,\theta_n}[\ln P(Y,z|\theta)]\\&=\arg\max_\theta Q(\theta|\theta_n) \end{aligned}$$

上式定义了一个函数 $Q(\theta|\theta_n)$ ，称为 $Q$ 函数。

上式完整表明了EM算法中的一步迭代中所需要的两个步骤：E-step，求期望；M-step，求极大值。有了上面的铺垫，下面介绍EM算法的流程：

输入：观测数据 $Y$ ，不可观测数据 $Z$；

输出：参数 $\theta$ ；

步骤：1. 给出参数初始化值 $\theta_0$ ；

2. E步：记 $\theta_n$ 为第 $n$ 次迭代后参数的估计值。在第 $n+1$ 次迭代的E步，求期望（ $Q$ 函数）

$$Q(\theta|\theta_n)=\mathbb E_{\textbf Z|\textbf Y,\theta_n}[\ln P(Y,z|\theta)]=\sum_zP(z|Y,\theta_n)\ln P(Y,z|\theta)$$

3. M步：求 $Q$ 函数的极大值点，来作为第 $n+1$ 次迭代所得到的参数估计值 $\theta_{n+1}$

$$\theta_{n+1}=\arg\max_\theta Q(\theta|\theta_n)$$

4. 重复上面两步，直至达到停机条件。

EM算法的收敛性定理

定理1：观测数据的似然函数 $P(Y|\theta)$ 通过EM算法得到的序列 $P(Y|\theta_n)(n=1,2,...)$ 单调递增：$P(Y|\theta_{n+1})\ge P(Y|\theta_n)$ 。

定理2：(1) 如果 $P(Y|\theta)$ 有上界，则 $L(\theta_n)=\ln P(Y|\theta_n)$ 收敛到某一值 $L^*$ ；

(2) 在 $Q$ 函数与 $L(\theta)$ 满足一定条件下，由EM算法得到的参数估计序列 $\theta_n$ 的收敛值 $\theta^*$ 是  $L(\theta)$ 的稳定点。

定理2中第二点的“条件”在大多数情况下都满足。只能保证收敛到稳定点，不能保证收敛到极大值点，因此EM算法受初值的影响较大。

使用EM算法求解三硬币模型

参考资料[2]给出了三硬币模型的描述：

假设有三枚硬币A、B、C，这些硬币正面出现的概率分别是 $\pi$ 、$p$ 、$q$ 。进行如下掷硬币试验： 先掷A，如果A是正面则再掷B，如果A是反面则再掷C。对于B或C的结果，如果是正面则记为1，如果是反面则记为0。进行 $N$ 次独立重复实验，得到结果。现在只能观测到结果，不能观测到掷硬币的过程，估计模型参数 $\theta=(\pi,p,q)$ 。

在这个问题中，实验结果是可观测数据 $Y=(y_1,...,y_N)$ ，硬币A的结果是不可观测数据 $Z=(z_1,...,z_N)$ 且 $z$ 只有两种可能取值1和0。

对于第 $j$ 次试验，

$$\begin{aligned} P(y_j|\theta)&= \sum_zP(y_j,z|\theta)\\&=\sum_zP(z|\theta)P(y_j|z,\theta)\\&=P(z=1|\theta)P(y_j|z=1,\theta)+P(z=0|\theta)P(y_j|z=0,\theta) \\&=\begin{cases} \pi p+(1-\pi )q, & \text{if }y_j=1;\\ \pi (1-p)+(1-\pi )(1-q), & \text{if }y_j=0.        \end{cases} \\&=\pi p^{y_j}(1-p)^{1-y_j}+(1-\pi )q^{y_j}(1-q)^{1-y_j} \end{aligned}$$

所以有

$$P(Y|\theta)=\prod_{j=1}^NP(y_j|\theta)=\prod_{j=1}^N (\pi p^{y_j}(1-p)^{1-y_j}+(1-\pi )q^{y_j}(1-q)^{1-y_j})$$

1. E-step，求期望（Q函数）：

$$\begin{aligned} Q(\theta|\theta_n)&=\sum_zP(z|Y,\theta_n)\ln P(Y,z|\theta)\\&=\sum_{j=1}^N\{ \sum_zP(z|y_j,\theta_n)\ln P(y_j,z|\theta)  \}\\&=\sum_{j=1}^N\{ P(z=1|y_j,\theta_n)\ln P(y_j,z=1|\theta) + P(z=0|y_j,\theta_n)\ln P(y_j,z=0|\theta) \} \end{aligned}$$

先求 $P(z|y_j,\theta_n)$ ，

$$P(z|y_j,\theta_n)=\begin{cases} \frac{\pi_n p_n^{y_j}(1-p_n)^{1-y_j}}{\pi_n p_n^{y_j}(1-p_n)^{1-y_j}+(1-\pi_n )q_n^{y_j}(1-q_n)^{1-y_j}}=\mu_{j,n} & \text{if }z=1; \\1-\mu_{j,n} & \text{if }z=0.  \end{cases}$$

再求 $P(y_j,z|\theta)=P(z|\theta)P(y_j|z,\theta)$ ，

$$P(y_j,z|\theta)=\begin{cases} \pi p^{y_j}(1-p)^{1-y_j} &\text{if }z=1;\\ (1-\pi )q^{y_j}(1-q)^{1-y_j} &\text{if }z=0. \end{cases}$$

因此，$Q$ 函数表达式为：

$$Q(\theta|\theta_n)=\sum_{j=1}^N\{\mu_{j,n}\ln [\pi p^{y_j}(1-p)^{1-y_j}]+(1-\mu_{j,n})\ln [(1-\pi )q^{y_j}(1-q)^{1-y_j}] \}$$

2. M-step，求 $Q$ 函数的极大值：

令 $Q$ 函数对参数求导数，并等于零。

$$\begin{aligned} \frac{\partial Q(\theta|\theta_n)}{\partial \pi}&=\sum_{j=1}^N\{\frac{\mu_{j,n}\ln [\pi p^{y_j}(1-p)^{1-y_j}]+(1-\mu_{j,n})\ln [(1-\pi )q^{y_j}(1-q)^{1-y_j}] }{\partial \pi}\}\\&=\sum_{j=1}^N\{ \mu_{j,n}\frac{p^{y_j}(1-p)^{1-y_j}}{\pi p^{y_j}(1-p)^{1-y_j}}+(1-\mu_{j,n})\frac{-q^{y_j}(1-q)^{1-y_j}}{(1-\pi )q^{y_j}(1-q)^{1-y_j}} \}\\&=\sum_{j=1}^N\{ \frac{\mu_{j,n}-\pi }{\pi (1-\pi)}\}\\&=\frac{(\sum_{j=1}^N\mu_{j,n})-n\pi }{\pi (1-\pi)} \end{aligned}$$

$$\begin{aligned}\frac{\partial Q(\theta_|\theta_n)}{\partial \pi}=0 &\implies \pi =\frac 1n\sum_{j=1}^N\mu_{j,n}\\ \therefore \pi_{n+1}&=\frac 1n\sum_{j=1}^N\mu_{j,n} \end{aligned}$$

$$\begin{aligned} \frac{\partial Q(\theta|\theta_n)}{\partial p}&=\sum_{j=1}^N\{\frac{\mu_{j,n}\ln [\pi p^{y_j}(1-p)^{1-y_j}]+(1-\mu_{j,n})\ln [(1-\pi )q^{y_j}(1-q)^{1-y_j}] }{\partial p}\}\\&=\sum_{j=1}^N\{ \mu_{j,n}\frac{\pi (y_jp^{y_j-1}(1-p)^{1-y_j}+p^{y_j}(-1)(1-y_j)(1-p)^{1-y_j-1})}{\pi p^{y_j}(1-p)^{1-y_j}}+0 \}\\&=\sum_{j=1}^N\{ \frac{\mu_{j,n}(y_j-p) }{p(1-p)}\}\\&=\frac{(\sum_{j=1}^N\mu_{j,n}y_j)-(p\sum_{j=1}^N\mu_{j,n}) }{p(1-p)} \end{aligned}$$

$$\begin{aligned}\frac{\partial Q(\theta_|\theta_n)}{\partial p}=0 &\implies p =\frac{\sum_{j=1}^N\mu_{j,n}y_j}{\sum_{j=1}^N\mu_{j,n}}\\ \therefore p_{n+1}&=\frac{\sum_{j=1}^N\mu_{j,n}y_j}{\sum_{j=1}^N\mu_{j,n}}\\q_{n+1}&=\frac{\sum_{j=1}^N(1-\mu_{j,n})y_j}{\sum_{j=1}^N(1-\mu_{j,n})} \end{aligned}$$

既然已经得到了三个参数的迭代式，便可给定初值，迭代求解了。

参考资料：

[1] The Expectation Maximization Algorithm: A short tutorial - Sean Borman

[2] 《统计学习方法》，李航

[3] 梯度下降和EM算法：系出同源，一脉相承 这是最近扫到的一篇，还没有看，感觉不错，有时间看一下～