机器学习之决策树（ID3 、C4.5算法）

声明：本篇博文是学习《机器学习实战》一书的方式路程，系原创，若转载请标明来源。

1 决策树的基础概念

决策树分为分类树和回归树两种，分类树对离散变量做决策树 ,回归树对连续变量做决策树。决策树算法主要围绕两大核心问题展开:第一, 决策树的生长问题 , 即利用训练样本集 , 完成决策树的建立过程。第二, 决策树的剪枝问题,即利用检验样本集 , 对形成的决策树进行优化处理。这里主要介绍分类树的两个经典算法：ID3算法和C4.5算法，他们都是以信息熵作为分类依据，ID3 是用信息增益，而C4.5 是利用信息增益率。并且都是单棵决策树。

1.1 生成决策树的过程

决策树的生产过程本质是对训练样本集的不断分组过程，其核心技术是测试属性选择问题。以下为算法推演过程：

设 S 是s 个数据样本的集合，假定类标号属性具有 m 个不同值, 定义 m 个不同类C_i(i =1 , … , m)，设 s_i是类C_i 中的样本数。由此可以得出样本集 S 对分类的平均信息量:

其中，P（C_p ）=C_i / S ，是任意样本属于C_i 的概率。注意：对数函数以2 为底, 其原因是信息用二进制编码。

再设训练样本集 S 除类标号属性之外的属性集为：A_i (j=1,... , k) ，决策树的构建过程就是使划分后不确定性逐渐减小的过程。以任意的离散属性 A _i为例。假设 A_i 存在 t 个不同的取值 a_q (1 ≤ q≤ t )。那么根据 A_i 的取值，不仅可以将 S 划分为S₁,S₂, ... ,S_t ，共 t 个子集,还可以任意子集 S_i 划分成 C₁,C₂, ... , C_m这 m 个子集，即一共划分为 m×t 个子集,每个子集 C_pq 表示在 A_i=a_q 的条件下属于第 p 类的样本集合，其中，1 ≤ p ≤ m , 1 ≤ q ≤ t.由此，选择离散的非类别属性A_i 进行划分后，样本集S 对分类的平均信息量为：

其中，P（C_q）= S_q / S，P(C_pq) = C_pq / S_{q .}

一般来讲，信息增益越大，说明如果用属性A来划分样本集合S，那么纯度会提升，因为我们分别对样本的所有属性计算增益情况，选择最大的来作为决策树的一个结点，或者可以说那些信息增益大的属性往往离根结点越近，因为我们会优先用能区分度大的也就是信息增益大的属性来进行划分。当一个属性已经作为划分的依据，在下面就不在参与竞选了，并且在当前的样本下利用剩下的属性再次计算信息增益来进一步选择划分的结点，ID3决策树就是这样建立起来的。那么利用 A_i 对 S 进行划分的信息增益量(information gain) f_G(S,A_i) 则等于使用 A_i 对 S 进行划分前后,不确定性下降的程度，即：

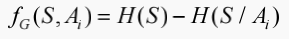
C4.5决策树的提出完全是为了解决ID3决策树的一个缺点，当一个属性的可取值数目较多时，那么可能在这个属性对应的可取值下的样本只有一个或者是很少个，那么这个时候它的信息增益是非常高的，这个时候纯度很高，ID3决策树会认为这个属性很适合划分，但是较多取值的属性来进行划分带来的问题是它的泛化能力比较弱，不能够对新样本进行有效的预测。由于 C4.5 算法是使用属性 A_i 对 S 进行划分的信息增益率等于信息增益量与分割信息量(split information)之比，即信息增益率：

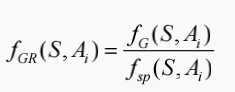
其中，f_sp(S,A_i)为分割信息量：

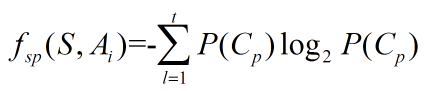
其中，P（C_p）= S_p / S.

1.2 决策树的修剪

决策树的修剪是针对训练数据过分拟合问题而提出来的 ,修剪方法通常利用统计方法删去最不可靠的分支(树枝), 以提高今后分类识别的速度和分类识别新数据的能力。其实质是消除训练集中的异常和噪声。过分拟合是指树的规模变的过大，即使训练误差在不断降低，但是检验误差开始增加的现象。

处理决策树归纳中的过分拟合问题的一般解决方法有两种：一、先剪枝（提前终止规则）：该方法通过提前停止分支生成过程, 即通过在当前节点上就判断是否需要继续划分该节点所含训练集来实现。一旦停止分支，当前节点就成为一个叶节点，该叶节点中可能包含多个不同类别的训练样本。在建造一个决策树时，可以利用统计上的重要性检测 χ² 或信息增益等来对分支生成情况进行评估。如果在一个节点上划分样本集时 , 会导致节点中样本数少于指定的阈值, 则要停止继续分解样本集合。但确定这样一个合理的阈值常常也比较困难 , 阈值过大会导致决策树过于简单化, 而阈值过小又会导致多余树枝无法修剪。二、后剪枝：该方法从一个“充分生长”树中 ,修剪掉多余的树枝。基于代价成本的修剪算法就是一个事后修剪方法, 被修剪的节点就成为一个叶节点 ,并将其标记为它所包含样本中类别个数最多的类别。而对于树中每个非叶节点, 计算出若该节点被修剪后所发生的预期分错误率 ;同时根据每个分支的分类错误率 ,以及每个分支的权重, 计算若该节点不被修剪时的预期分类错误率;如果修剪导致预期分类错误率变大, 则放弃修剪, 保留相应节点的各个分支, 否则就将相应节点分支修剪删去。在产生一系列经过修剪的决策树候选之后,利用一个独立的测试数据集, 对这些经过修剪的决策树的分类准确性进行评价 ,保留下预期分类错误率最小的决策树。除了利用预期分类错误率进行决策树修剪之外, 还可以利用决策树的编码长度来进行决策树的修剪。所谓最佳修剪树就是编码长度最短的决策树 ,这种修剪方法利用最短描述长度(Minimum Description Length , 简称 M DL)原则来进行决策树的修剪。该原则的基本思想就是:最简单的就是最好的。与基于代价成本方法相比, 利用 M DL进行决策树修剪时无需额外的独立测试数据集。当然事前修剪可以与事后修剪相结合, 从而构成一个混合的修剪方法。事后修剪比事前修剪需要更多的计算时间 ,从而可以获得一个更可靠的决策树。

2 ID3 算法的Python代码实现

注：程序中使用数据样本集满足的条件，第一个是数据必须是一种由列表元素组成的列表，而且所有的列表元素都要具有相同的数据长度；第二个是数据的最后一列或者每个实例的最后一个元素是当前实例的类别标签（类标号）。

2.1 计算数据样本集的类标号的平均信息量（香农熵）

代码实现的公式：

代码如下：

 from math import log

 def calcShannonEnt(dataSet):

     numEntries = len(dataSet)

     labelCounts = {}

     for featVec in dataSet:

         currentLabel = featVec[-1] # 提取类标号的属性值

         # 把类标号不同的属性值及其个数存入字典中

         if currentLabel not in labelCounts .keys():

             labelCounts [currentLabel ]=0

         labelCounts [currentLabel]+=1

     shannonEnt = 0.0

     # 计算类标号的平均信息量，如公式中H（S）

     for key in labelCounts :

         prob = float(labelCounts [key])/numEntries

         shannonEnt -= prob * log(prob,2)

     return shannonEnt

代码解释：

1. log()方法返回x的自然对数，对于x>0。另外，可以通过log(x[, base])来设置底数，如 log(x, 10) 表示以10为底的对数。

2.2 提取特定的特征的属性值数据

筛选给定的特征的属性值，并组合成一个新的列表。

代码如下：

 # 按照给定特征划分数据集,把符合给定属性值的对象组成新的列表

 def splitDataSet(dataSet,axis,value):

     retDataSet = []

     for featVec in dataSet:

         # 选择符合给定属性值的对象

         if featVec[axis] == value:

             reduceFeatVec = featVec[:axis] # 对对象的属性值去除给定的特征的属性值

             reduceFeatVec.extend(featVec[axis+1:])

             retDataSet.append(reduceFeatVec ) # 把符合且处理过的对象添加到新的列表中

     return retDataSet

代码解释：

1 . 函数splitDataSet() 的参数，dataSet 是数据样本集合，axis 是特征（属性），value 是属性值。

2 . extend() 函数用于在列表末尾一次性追加另一个序列中的多个值（用新列表扩展原来的列表），该函数没有返回值，但会在已存在的列表中添加新的列表内容。

2.3 选择最好的数据集的划分方式

实现公式：

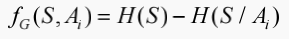
代码如下：

 # 选取最佳特征的信息增益，并返回其列号

 def chooseBestFeaturesplit(dataSet):

     numFeatures = len(dataSet[0])-1  # 获得样本集S 除类标号之外的属性个数，如公式中的k

     baseEntropy = calcShannonEnt(dataSet) # 获得类标号属性的平均信息量，如公式中H(S)

     bestInfoGain = 0.0 # 对最佳信息增益的初始化

     bestFeature = -1 # 最佳信息增益的属性在样本集中列号的初始化

     # 对除类标号之外的所有样本属性一一计算其平均信息量

     for i in range(numFeatures ):

         featList = [example[i] for example in dataSet] # 提取第i 个特征的所有属性值

         uniqueVals = set(featList ) # 第i 个特征所有不同属性值的集合，如公式中 aq

         newEntropy = 0.0 # 对第i 个特征的平均信息量的初始化

         # 计算第i 个特征的不同属性值的平均信息量，如公式中H（S| Ai）

         for value in uniqueVals:

             subDataSet = splitDataSet(dataSet,i,value ) # 提取第i 个特征，其属性值为value的对象集合

             prob = len (subDataSet )/float(len(dataSet)) # 计算公式中P（Cpq）的概率

             newEntropy += prob * calcShannonEnt(subDataSet ) # 第i个特征的平均信息量，如 公式中H（S| Ai）

         infoGain = baseEntropy - newEntropy  # 第i 个的信息增益量

         if (infoGain > bestInfoGain ): # 选取最佳特征的信息增益，并返回其列号

             bestInfoGain  = infoGain

             bestFeature = i

     return bestFeature

代码解释：

1. 对于第十行代码的理解给一个简单例子：

>>> list = [i for i in range(10)]

>>> list

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

3 创建决策树

由于数据样本中的特征的数量可能多于两个，因此可能存在两个分支及以上的数据集划分，利用递归调用的方式解决特征数量大的问题。递归结束的条件是：程序遍历完所有的划分数据集的特征，或者每个分支下的所有实例（对象）都具有相同的分类（类标号）。对于前者需要从余下的类标号中选择重复次数最多的一个作为叶子节点，后者则直接是叶子节点。

3.1 从程序遍历完之后的类标号的属性值中选择叶子节点

代码如下：

 # 选择列表中重复次数最多的一项

 def majorityCnt(classList):

     classCount= {}

     for vote in classList :

         if vote not in classCount .keys():

             classCount [vote] =0

         classCount[vote] += 1

     sortedClassCount = sorted(classCount.iteritems() ,

                                   key=operator.itemgetter(1),

                                   reverse= True ) # 按逆序进行排列，并返回由元组组成元素的列表

     return sortedClassCount[0][0]

3.2 创建决策树的代码实现

代码如下：

 # 创建决策树

 def createTree(dataSet,Labels):

     labels = Labels[:] ; classList = [example[-1] for example in dataSet ] # 再建列表labels是为防止最初的特征列表；获得样本集中的类标号所有属性值

     if classList.count(classList [0]) == len(classList): # 类标号的属性值完全相同则停止继续划分

         return classList[0]

     if len(dataSet[0]) == 1: # 遍历完所有的特征时，仍然类标号不同的属性值，则返回出现次数最多的属性值

         return majorityCnt(classList)

     bestFeat = chooseBestFeaturesplit(dataSet) # 选择划分最佳的特征,返回的是特征在样本集中的列号

     bestFeatLabel = labels[bestFeat]  # 提取最佳特征的名称

     myTree = {bestFeatLabel :{}} # 创建一个字典，用于存放决策树

     del(labels[bestFeat]) # 从特征列表中删除已经选择的最佳特征

     featValues = [example[bestFeat] for example in dataSet ] # 提取最佳特征的所有属性值

     uniqueVals = set(featValues ) # 获得最佳特征的不同的属性值

     for value in uniqueVals :

         subLabels = labels[:] #  把去除最佳特征的特征列表赋值于subLabels

         myTree [bestFeatLabel][value] = createTree(splitDataSet(dataSet ,bestFeat ,value ),

                                                    subLabels ) # 递归调用createTree()函数

     return myTree

代码解释：

对于第16行的递归调用的个人理解是：从第一个最佳特征开始进行分支，分支的结束条件就是递归结束的条件，不满足分支结束条件的则继续分支。第二次分支是对上次分支所有不满足结束条件的最佳特征的不同属性值的分支，改变的条件有样本集是去除上次最佳特征的所有属性值的新的样本集和去除最佳特征的新的特征列表，再根据新的样本集和特征列表再次选出最佳特征进行分支，依次分支，直到所有分支都满足分支结束的条件为止。例如：(1)样本集的第一个最佳特征为 A_i , 其属性值有a {a₁,a₂, ... ,a_k}，假设a₁、a₂ 满足结束条件则成为一个叶子节点；(2)余下的a₃, ... ,a_k，作为新的分支的“根节点”，在属性值为a₃ 的集合中从新的样本集中选出最佳特征A_j ，其属性值有b {b₁,b₂, ... ,b_m}，假设b₁ 满足结束条件则成为一个叶子节点；余下的b₂、b₃, ... ,b_m，作为新的分支的“根节点”，重复步骤（1），直到所有分支都满足分支结束的条件为止。(3)再在属性值为a₄ 的集合中从新的样本集中选出最佳特征A_r，重复步骤（2）。

3.3 决策树的存储

构造决策树是很耗时的任务，然而用创建好的决策树解决分类问题，则可以很快完成。因此，为了节省计算时间，最好把每次执行分类时调用已经构造好的决策树。为了解决这个问题，需要用Python 模块pickle 序列化对象，其可以在磁盘中保存对象，并在需要的时候进行调用。分两部分操作：一、把决策树以文件的形式存入磁盘中；二、把磁盘中的决策树读取到程序中。

3.3.1 把决策树以文件的形式存入磁盘中

代码如下：

 def storeTree(inputTree,filename):

     import pickle

     fw = open(filename,'w')

     pickle.dump(inputTree ,fw)

     fw.close()

代码解释：pickle.dump(obj, file, [,protocol])

将对象obj保存到文件file中去。

protocol为序列化使用的协议版本，0：ASCII协议，所序列化的对象使用可打印的ASCII码表示；1：老式的二进制协议；2：2.3版本引入的新二进制协议，较以前的更高效。其中协议0和1兼容老版本的python。protocol默认值为0。

　　　　　file：对象保存到的类文件对象。file必须有write()接口， file可以是一个以'w'方式打开的文件或者一个StringIO对象或者其他任何实现write()接口的对象。如果protocol>=1，文件对象需要是二进制模式打开的。

3.3.2 把磁盘中的决策树读取到程序中

代码如下

 def grabTree(filename):

     import pickle

     fr = open(filename)

     return pickle.load(fr)

代码解释：

pickle.load(file) 从file中读取一个字符串，并将它重构为原来的python对象。

3.4 测试决策树

代码如下:

 # 使用决策树的分类函数

 def classify(inputTree,featLabels,testVec):

     firstStr = inputTree.keys()[0]  # 获得距离根节点最近的最佳特征

     secondDict = inputTree[firstStr ]  # 最佳特征的分支

     featIndex = featLabels .index(firstStr ) # 获取最佳特征在特征列表中索引号

     for key in secondDict .keys(): # 遍历分支

         if testVec [featIndex ] == key: # 确定待查数据和最佳特征的属性值相同的分支

             if type(secondDict [key]).__name__ == 'dict': # 判断找出的分支是否是“根节点”

                 classLabel = classify(secondDict[key],featLabels ,testVec) # 利用递归调用查找叶子节点

             else:

                 classLabel  = secondDict [key]  # 找出的分支是叶子节点

     return classLabel

代码解释：

1 函数classify() 参数inputTree 是决策树的字典形式，featLabels 是样本集的所有特征的列表，testVec 是测试的对象

2 递归调用在决策树中对内部节点寻找符合的叶子节点。

3.5 使用决策树预测数据

数据样本的背景：在钢铁厂中 , 轧辊是易磨损的, 且价格比较高 ,需要经常更换 , 使用成本比较高。而且一旦轧辊出了问题, 可能会造成很大的损失。正确的决策是否更换某一轧辊, 使得公司的效益最大化, 具有重要的现实意义。利用决策树分类在钢铁厂轧辊选择, 用于决策是否更换某一轧辊的情况。数据是从钢铁厂的轧辊更换的数据库中抽取出的部分数据, 含有 5 个属性:役龄、价格、是否关键部件、磨损程度和是否更换。利用这样的少量的数据来说明决策树分类在钢铁厂轧辊选择中的应用。

对收集的数据进行建立库

代码如下：

 def createDataSet1():

     dataSet = [[u'小于等于5',u'高',u'否',u'一般',u'否'],

                [u'小于等于5', u'高', u'否', u'好', u'否'],

                [u'5到10', u'高', u'否', u'一般', u'否'],

                [u'大于等于10', u'中', u'否', u'一般', u'是'],

                [u'大于等于10', u'低', u'是', u'一般', u'是'],

                [u'5到10', u'中', u'否', u'好', u'否'],

                [u'5到10', u'高', u'是', u'一般', u'是'],

                [u'小于等于5', u'中', u'否', u'一般', u'否'],

                [u'5到10', u'中', u'否', u'好', u'否'],

                [u'大于等于10', u'高', u'是', u'好', u'是'],

                [u'5到10', u'低', u'是', u'一般', u'是'],

                [u'小于等于5', u'中', u'是', u'一般', u'是'],

                [u'小于等于5', u'低', u'是', u'一般', u'是'],

                [u'大于等于10', u'中', u'是', u'好', u'是']]

     labels = [u'役龄',u'价格',u'是否关键部件',u'磨损程度']

     return dataSet ,labels

利用决策树对未知对象的预测，如一个轧钢的数据为：役龄为（=<5）、价格为高、不是关键部件、磨损程度一般。

代码如下

 def test_tree():

    dataSet,labels = createDataSet1()

    myTree = createTree(dataSet ,labels)

    print u'决策树：'

    print json.dumps(myTree , encoding="UTF-8", ensure_ascii=False, sort_keys=False, indent=4)# 把字典中的中文显示出来

    storeTree(myTree ,'zhagang.txt')

    Label = classify(grabTree('zhagang.txt'),labels,[u'小于等于5',u'高',u'否',u'一般'] )

    print u'--------测试结果---------'

    print u'轧钢是否更换： %s' % Label

运行结果：

结果符合现实情况，由于数据量小，不需要修剪；没有更多的检测样本，对这个决策树的质量不好评定。

到这里基本上把决策树的ID3 算法说的比较清晰了，我是看了几篇关于ID3 算法的论文及其他资料，把决策树的ID3 算法和C4.5 算法的原理，根据自己的理解重新梳理一遍，能力有限只能做到这样了。又把ID3算法用python代码实现，并对代码详细地进行注解，一方面可以加深自己对代码的理解，另一方面可以为同为小白的同学共勉。打算下篇文章使决策树以图形的形式展现，做决策树的图形可视化。