斐波那契数列—Java

斐波那契数列想必大家都知道吧，如果不知道的话，我就再啰嗦一遍，

斐波那契数列为：1 2 3 5 8 13 ...，也就是除了第一项和第二项为1以外，对于第N项，有f(N)=f(N-1)+f(N-2)。

下面我用三种方法实现这个函数，分别是：递归，循环，矩阵。

递归方法：

public class Feibo {
   //递归方法
    public static int recFeiBo(int n) {
        if(n<=0) {
            return 0;
        }

        if(n==1 || n==2) {
            return 1;
        }

        return recFeiBo(n-1) + recFeiBo(n-2);
    }

     public static void main(String[] args) {
        System.out.println(recFeiBo(6));
    }
}

循环方法：

public class Feibo{
    public static int recFeiBo(int n) {
        if(n<=0) {
            return 0;
        }

        if(n==1 || n==2) {
            return 1;
        }

        int pre =1;
        int temp =0;
        int res =1;

        for(int i=1; i<=n-2; i++) {
            temp = res;
            res+=pre;
            pre = temp;
        }

        return res;
    }

    public static void main(String[] args) {
        System.out.println(recFeiBo(6));
    }
}

矩阵的方法：

不知道你们有没有发现：

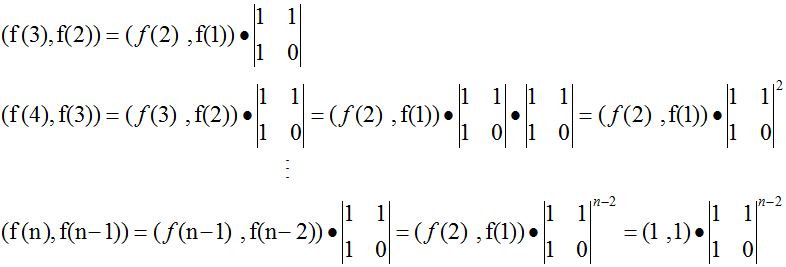
所以，最终求第N项数，就转化为求矩阵的n-2次方。

public class Feibo{
    public static int recFeiBo(int n) {
        if(n<=0) {
            return 0;
        }
        if(n==1 || n==2) {
            return 1;
        }

        int[][] baseMatrix = {{1,1},{1,0}};
        int[][] res = matrixPower(baseMatrix, n-2);
        return res[0][0] + res[1][0];
    }

    public static int[][] matrixPower(int[][] m, int n) {
        int[][] temp = m;
        int[][] res = new int[m.length][m[0].length];

        for(int i=0; i<m.length; i++) {
            res[i][i] = 1;
        }
        //n左移一位，并赋值给n
        //下面的for循环是用来快速的求解矩阵的n次方的。可以参考我下一篇关于如何快求解高次方
        for(;n!=0; n>>=1) {
            //判断第0位是不是1
            if((n&1)!=0) {
                res = multiMtrix(res,temp);
            }
            temp= multiMtrix(temp, temp);
        }

        return res;
    }

    private static int[][] multiMtrix(int[][] m1, int[][] m2) {
        int[][] res = new int[m1.length][m2[0].length];
        for(int i=0; i<m1.length; i++) {
            for(int j=0; j<m2[0].length; j++) {
                for(int k=0; k<m2.length; k++) {
                    res[i][j] += m1[i][k]*m2[k][j];
                }
            }
        }
        return res;
    }

    public static void main(String[] args) {
        System.out.println(recFeiBo(6));
    }
}

其实斐波那契额数列问题就是可以总结为一类问题，就是让你求的当前值可以用函数表示的，f(n)=f(n-1)+f(n-2),这类问题你都可以用矩阵的方式去实现，比如爬楼梯问题，有n阶楼梯，每次只能跨1阶或2阶，归结出来就是s(n)=s(n-1)+s(n-2)，初始值s(1)=1,s(2)=2.