AHUACM寒假集训I(基础数据结构+串串)
H.超级钢琴
题目大意:
求出一个长N序列中所有长度在L到R的子序列中序列和最大的K个,并求这K个的和
思路:
暴力的话可以求出所有满足要求的子序列然后排序,然后显然会T。
所以我们可以考虑对最大值一个个求解,求出一个最大值后删去之,继续求剩下的里面的最大值,总共求出K个即可。
我们先做一个前缀和,然后枚举左端点
S
[
i
]
S[i]
S[i],右端点
S
[
j
]
S[j]
S[j]在一个区间内,我们可以求出右端点的最大值也就能求出当前左端点下的最大值,我们把每个左端点这样求出的值加入堆内,然后我们弹出了这些中最大的之后,如果弹出的是
S
[
i
]
S[i]
S[i]下的最大值,那么我们把这个最大值删去就要维护
S
[
i
]
S[i]
S[i]的次大值,那么要怎么做呢,记录
S
[
i
]
S[i]
S[i]的右端点决策集合为
[
l
,
r
)
[l,r)
[l,r),假设我们弹出的最大值右端点位于
m
p
o
s
mpos
mpos,于是
S
[
i
]
S[i]
S[i]下的次大值的右端点就一定在
[
l
,
m
p
o
s
)
[l,mpos)
[l,mpos),
[
m
p
o
s
+
1
,
r
)
[mpos+1,r)
[mpos+1,r)当中,我们把他们都加入堆中即可。
RMQ用ST表可以
O
(
1
)
O(1)
O(1)查询。弹出,插入堆的操作不超过3K次
所以我们发现ST表+堆也可以求静态区间第K大
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<LL, int> PII;
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxn = 500010;
int N, K, L, R;
int A[maxn], S[maxn], ST[maxn][30], STpos[maxn][30];//STpos维护区间最大值的下标
void MAX_init(int n)
{
for (int i = 0; i < n; i++)
{
ST[i][0] = S[i];
STpos[i][0] = i;
}
for (int j = 1; (1 << j) <= n; j++)
{
for (int i = 0; i + (1 << j) - 1 < n; i++)
{
if (ST[i][j - 1] > ST[i + (1 << (j - 1))][j - 1])
{
ST[i][j] = ST[i][j - 1];
STpos[i][j] = STpos[i][j - 1];
}
else
{
ST[i][j] = ST[i + (1 << (j - 1))][j - 1];
STpos[i][j] = STpos[i + (1 << (j - 1))][j - 1];
}
}
}
}
int MAX(int l, int r)//[l,r)
{
if (l >= r)
return 0;
int k = floor(log2(r - l));
if (ST[l][k] > ST[r - (1 << k)][k])
return STpos[l][k];
else
return STpos[r - (1 << k)][k];
}
struct node {
int b, l, r, mpos;//[l,r)
node(int b, int l, int r) :b(b), l(l), r(r) { mpos = MAX(l, r); }
bool operator<(const node& rhs) const
{
return S[mpos] - S[b - 1] < S[rhs.mpos] - S[rhs.b - 1];
}
};
priority_queue<node>que;
void solve()
{
for (int i = 1; i <= N; i++)
S[i] = S[i - 1] + A[i];
MAX_init(N + 1);
LL ans = 0;
int cnt = 0;
for (int i = 1; i <= N; i++)
{
if (i + L - 1 > N)
break;
que.push(node(i, i + L - 1, min(i + R, N + 1)));
}
while (true)
{
node e = que.top();
que.pop();
ans += S[e.mpos] - S[e.b - 1];
cnt++;
if (cnt == K)
break;
if (e.mpos != e.l)
que.push(node(e.b, e.l, e.mpos));
if (e.mpos + 1 != e.r)
que.push(node(e.b, e.mpos + 1, e.r));
}
cout << ans << endl;
}
int main()
{
IOS;
cin >> N >> K >> L >> R;
for (int i = 1; i <= N; i++)
cin >> A[i];
solve();
return 0;
}
I.异或和
题目大意:
给一个长为N的序列, 求该序列所有子序列和的异或和,
思路:
首先我们肯定按位考虑,对于某一位,如果1的个数为奇数,这一位就对最后答案有贡献,否则没有,我们先对原序列做一个前缀和,然后我们先从低到高位枚举各位,每一位枚举所有右端点
S
[
i
]
S[i]
S[i],另外用一个数组
b
[
i
]
b[i]
b[i],记录当前
S
[
i
]
S[i]
S[i]在当前枚举位-1位到第0位这一段二进制数的数值,我们只需要统计如下的左端点
S
[
j
]
S[j]
S[j]即可,因为只有下述情况会在当前这一位产生1:
1)当前位为0,那么我们的
S
[
j
]
S[j]
S[j]的当前位为1并且低处各位二进制数的数值必须小于
S
[
i
]
S[i]
S[i]对应部分的数值,或者
S
[
j
]
S[j]
S[j]的当前位为0并且低处各位二进制数的数值必须大于
S
[
i
]
S[i]
S[i]对应部分的数值。
2)当前位为1,那么我们的S[j]的当前位为1并且低处各位二进制数的数值必须大于
S
[
i
]
S[i]
S[i]对应部分的数值,或者
S
[
j
]
S[j]
S[j]的当前位为0并且低处各位二进制数的数值必须小于
S
[
i
]
S[i]
S[i]对应部分的数值。
我们可以用一个权值树状数组来维护各个
b
[
j
]
b[j]
b[j]值对应的前面一位的0,1的个数,然后可以轻松统计上面两种情况,具体实现见注释:
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<LL, int> PII;
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxn = 1000010;
int dat[maxn][2], n;
void add(int i, int t, int x)//维护已出现各B[j]最高位再前一位是1/0的次数
{
while (i <= n)
{
dat[i][t] += x;
i += i & (-i);
}
}
int sum(int i, int t)
{
int ans = 0;
while (i > 0)
{
ans += dat[i][t];
i -= i & (-i);
}
return ans;
}
int N, A[maxn], B[maxn];
int S[maxn];
void solve()
{
int ans = 0;
n = 1000005;
for (int i = 1; i <= N; i++)
S[i] = S[i - 1] + A[i];
for (int i = 0; i < 20; i++)
{
memset(dat, 0, sizeof(dat));
add(1, 0, 1);//偏移1
int cnt = 0;
for (int j = 1; j <= N; j++)//考虑以S[j]为被减数
{
int tmp = (S[j] >> i) & 1;
int now = sum(B[j] + 1, tmp ^ 1) + sum(n, tmp) - sum(B[j] + 1, tmp);//产生1的个数
if (now % 2)
cnt ^= 1;
add(B[j] + 1, tmp, 1);//处理新来的B[j]
if (tmp)
B[j] |= (1 << i);//处理过的B[j]再加一位
}
if (cnt)
ans |= (1 << i);
}
cout << ans << endl;
}
int main()
{
IOS;
cin >> N;
for (int i = 1; i <= N; i++)
cin >> A[i];
solve();
return 0;
}
K.动物园
luoguP2375
题目大意:
给定
N
(
N
≤
5
)
N(N\leq5)
N(N≤5)个串,串的长度
≤
1
0
6
\leq10^6
≤106,令
n
u
m
[
i
]
num[i]
num[i]为串上前
i
i
i个字符中互不重叠的公共前后缀数量,求
∏
i
=
1
S
(
n
u
m
[
i
]
+
1
)
\prod_{i=1}^{S}(num[i]+1)
∏i=1S(num[i]+1)
m
o
d
mod
mod
1
0
9
+
7
10^9+7
109+7
思路:
注意到每次
j
=
n
e
x
t
[
j
]
j=next[j]
j=next[j],
j
j
j就会来到前长为
j
j
j的前缀当中更短的一个非自身的公共前后缀中前缀的尾后位置,即对
j
j
j不断取
n
e
x
t
[
j
]
next[j]
next[j]知道
j
=
0
j=0
j=0的次数我们记为
a
n
s
[
j
]
ans[j]
ans[j],也就是长为
j
j
j的前缀当中公共前后缀的数量(包括自身),即
a
n
s
[
1
]
=
1
ans[1]=1
ans[1]=1,其实也就相当于
j
j
j在
K
M
P
KMP
KMP的
f
a
i
l
fail
fail树上的深度,我们可以在求
n
e
x
t
[
]
next[]
next[]时递推得到
a
n
s
[
]
ans[]
ans[]。
之后我们只需要求出
j
j
j取若干次
n
e
x
t
[
j
]
next[j]
next[j]后
j
∗
2
≤
i
+
1
j*2\leq i+1
j∗2≤i+1时的
a
n
s
[
j
]
ans[j]
ans[j]即为
n
u
m
[
i
]
num[i]
num[i]了。
为什么算入了自身的
a
n
s
[
j
]
ans[j]
ans[j]就是不算入自身的
n
u
m
[
i
]
num[i]
num[i]了呢?因为
j
∗
2
≤
i
+
1
j*2\leq i+1
j∗2≤i+1,所以此时
a
n
s
[
j
]
ans[j]
ans[j]算入的自身就是一个不是自身的长为
i
i
i的前缀的一个公共前后缀中的前缀了。
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<LL, int> PII;
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxn = 1000010;
int nxt[maxn], ans[maxn];
int N;
string S;
void buildNext(string P)
{
int m = P.length();
nxt[0] = -1, nxt[1] = 0;
ans[0] = 0, ans[1] = 1;
for (int i = 1, j = 0; i < m; i++)
{
while (j > 0 && P[i] != P[j])
j = nxt[j];
if (P[i] == P[j])
j++;
nxt[i + 1] = j;
ans[i + 1] = ans[j] + 1;
}
}
void solve()
{
buildNext(S);
LL cnt = 1;
for (int i = 1, j = 0; i < S.length(); i++)
{
while (j > 0 && S[i] != S[j])
j = nxt[j];
if (S[i] == S[j])
j++;
while (j * 2 > i + 1)
j = nxt[j];
cnt = (cnt * (LL)(ans[j] + 1)) % mod;
}
cout << cnt << endl;
}
int main()
{
IOS;
cin >> N;
while (N--)
{
cin >> S;
solve();
}
return 0;
}
L.Matching
luoguP4696
题目:

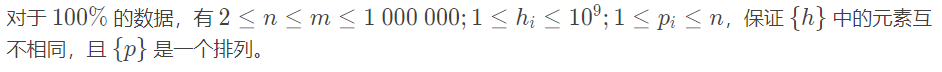
思路:
对于排列
P
P
P,如果
H
H
H的某个字串要与之符合,该字串内第
P
[
i
]
P[i]
P[i]个元素的相对排名必须是
i
i
i,即对于
P
=
[
2
,
1
,
5
,
3
,
4
]
P=[2,1,5,3,4]
P=[2,1,5,3,4],符合要求的字串内元素的相对排名为
A
=
[
2
,
1
,
4
,
5
,
3
]
A=[2,1,4,5,3]
A=[2,1,4,5,3],那么我们可以用
K
M
P
KMP
KMP改为匹配字串内的相对排名来解决,动态维护区间内的相对排名我们可以用
B
I
T
BIT
BIT来解决,对于序列
A
A
A,我们可以求出
A
[
i
]
A[i]
A[i]前面有多少个数小于它,记这个序列为
S
S
S,对于样例,
S
=
[
0
,
0
,
2
,
3
,
2
]
S=[0,0,2,3,2]
S=[0,0,2,3,2],这个序列也能够唯一对应一个排名序列,而且很容易用
B
I
T
BIT
BIT维护,于是我们对两个原序列的这个序列去进行匹配即可,另外还要先将
H
H
H离散化。
在求
n
x
t
[
]
nxt[]
nxt[]的时候,如果是
i
,
j
i,j
i,j一起向前跳,那么加入
i
i
i的贡献,否则如果需要
j
=
n
x
t
[
j
]
j=nxt[j]
j=nxt[j],就要减去位于
[
i
−
j
,
i
−
n
x
t
[
j
]
−
1
]
[i-j,i-nxt[j]-1]
[i−j,i−nxt[j]−1]的贡献,因为要进行匹配的段缩短到了
[
i
−
n
x
t
[
j
]
,
i
]
[i-nxt[j],i]
[i−nxt[j],i],这个画一下图会更好理解。
在匹配的时候的操作也类似,这样我们可以
O
(
N
+
M
l
o
g
N
)
O(N+MlogN)
O(N+MlogN)求得
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<LL, int> PII;
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxn = 1000010;
int N, M, P[maxn], H[maxn], S[maxn], nxt[maxn];
int dat[maxn], n;
vector<int>ans;
void add(int i, int x)
{
while (i <= n)
{
dat[i] += x;
i += i & (-i);
}
}
int sum(int i)
{
int ans = 0;
while (i > 0)
{
ans += dat[i];
i -= i & (-i);
}
return ans;
}
void compress()
{
vector<int>xs;
for (int i = 1; i <= M; i++)
xs.push_back(H[i]);
sort(xs.begin(), xs.end());
xs.erase(unique(xs.begin(), xs.end()), xs.end());
for (int i = 1; i <= M; i++)
H[i] = upper_bound(xs.begin(), xs.end(), H[i]) - xs.begin();
}
void solve()
{
n = M;
compress();
for (int i = 1; i <= N; i++)
{
S[i] = sum(P[i]);
add(P[i], 1);
}
nxt[1] = 0;
memset(dat, 0, sizeof(dat));
for (int i = 2, j = 0; i <= N; i++)
{
while (j > 0 && sum(P[i]) != S[j + 1])
{
for (int k = i - j; k <= i - nxt[j] - 1; k++)
add(P[k], -1);
j = nxt[j];
}
if (sum(P[i]) == S[j + 1])
{
add(P[i], 1);
j++;
}
nxt[i] = j;
}
memset(dat, 0, sizeof(dat));
for (int i = 1, j = 0; i <= M; i++)
{
while (j > 0 && (j == N || sum(H[i]) != S[j + 1]))
{
for (int k = i - j; k <= i - nxt[j] - 1; k++)
add(H[k], -1);
j = nxt[j];
}
if (sum(H[i]) == S[j + 1])
{
add(H[i], 1);
j++;
}
if (j == N)
ans.push_back(i - N + 1);
}
cout << ans.size() << endl;
for (auto& c : ans)
cout << c << ' ';
cout << endl;
}
int main()
{
IOS;
cin >> N >> M;
int num;
for (int i = 1; i <= N; i++)
{
cin >> num;
P[num] = i;
}
for (int i = 1; i <= M; i++)
cin >> H[i];
solve();
return 0;
}
M.企鹅QQ
luoguP4503
题目大意:
N
(
N
≤
30000
)
N(N\leq30000)
N(N≤30000)个长为
L
(
L
≤
200
)
L(L\leq200)
L(L≤200)的串,所有串都不同,求有多少对串有且仅有1个对应位置上字符不同。
思路:
因为所有串互不相同,所以对于两个串,如果挖去同一个位置上的字符后二者相同,则说明这一对串满足条件。因此我们可以枚举挖去的位置,之后对所有串进行匹配。
我们可以分别从前往后和从后往前处理每个字符串的hash值,挖掉某一字符的hash值就是把剩下两部分的hash值拼起来,这样可以在
O
(
L
N
)
O(LN)
O(LN)预处理后
O
(
1
)
O(1)
O(1)得到,我们枚举每个位置字符得到删掉当前位置所有的hash值之后排个序,再遍历一遍算出答案即可,总的复杂度
O
(
N
L
l
o
g
N
)
O(NLlogN)
O(NLlogN)
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<LL, int> PII;
//#define int LL
#define lc p*2+1
#define rc p*2+2
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxn = 30010;
const int maxl = 210;
int N, L, S;
string str[maxn];
ULL hash1[maxn][maxl], hash2[maxn][maxl];
ULL d[maxn];
void solve()
{
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= L; j++)
hash1[i][j] = hash1[i][j - 1] * 131 + str[i][j - 1];//->
for (int j = L; j >= 1; j--)
hash2[i][j] = hash2[i][j + 1] * 13331 + str[i][j - 1];//<-
}
int ans = 0;
for (int j = 1; j <= L; j++)
{
for (int i = 1; i <= N; i++)
d[i] = hash1[i][j - 1] * mod + hash2[i][j + 1] * MOD;
sort(d + 1, d + 1 + N);
int c = 1;
for (int i = 2; i <= N; i++)
{
if (d[i] == d[i - 1])
{
ans += c;
c++;
}
else
c = 1;
}
}
cout << ans << endl;
}
int main()
{
IOS;
cin >> N >> L >> S;
for (int i = 1; i <= N; i++)
cin >> str[i];
solve();
return 0;
}
Acwing145.超市
N
(
1
≤
N
≤
1
0
4
)
N(1\leq N\leq10^4)
N(1≤N≤104)个商品,每个商品有利润
p
i
(
1
≤
p
i
≤
1
0
4
)
p_{i}(1\leq p_{i}\leq10^4)
pi(1≤pi≤104),保质期
d
i
(
1
≤
d
i
≤
1
0
4
)
d_{i}(1\leq d_{i}\leq10^4)
di(1≤di≤104),每天仅可购买一个商品,过期的商品不能再买,求购买商品可以获得的最大收益。
题目大意:
思路
反悔型贪心,按保质期从小到大考虑, 用一个堆来维护已经购买的商品的利润,如果在保质期内que.size()<d就先买,如果不在保质期内,就与已购买的利润最小的比较,如果利润大于它,就拿出最小的,改为购买这一个。
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
//#define int LL
#define lch p*2+1
#define rch p*2+2
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxn = 10010;
int N, ans;
PII A[maxn];
void solve()
{
priority_queue<int, vector<int>, greater<int>> que;
sort(A + 1, A + N + 1);
for (int i = 1; i <= N; i++)
{
if (que.size() >= A[i].first)
{
int k = que.top();
if (A[i].second > k)
{
que.pop();
que.push(A[i].second);
}
}
else
que.push(A[i].second);
}
while (!que.empty())
{
ans += que.top();
que.pop();
}
cout << ans << endl;
}
int main()
{
IOS;
while (cin >> N)
{
ans = 0;
for (int i = 1; i <= N; i++)
cin >> A[i].second >> A[i].first;
solve();
}
return 0;
}
luoguP4103.大工程
传送门
题目大意:
一颗
n
(
1
≤
n
≤
1
0
6
)
n(1\leq n\leq10^6)
n(1≤n≤106)的树,所有边的权值都为
1
1
1,
q
(
1
≤
q
≤
5
×
1
0
4
)
q(1\leq q\leq5\times10^4)
q(1≤q≤5×104)次询问,每次询问给出
k
(
∑
k
≤
2
n
)
k(\sum k\leq2n)
k(∑k≤2n)个节点,为这些节点两两修一条路,每条路的费用为原树上两点的最短路径长度,求总费用,单条路径的最小费用和最大费用。
思路:
由于总的
k
k
k很小,所以我们可以对每次询问去建立一颗虚树,把所有需要修路的点设为关键点。对于总费用,我们考虑虚树上每条边的贡献,虚树上每条边的长度就是原树上两点的深度差,对于每条边的两端点记为
f
a
,
s
o
n
fa,son
fa,son,以
v
v
v为根的子树内关键点的个数为
v
k
e
y
s
[
v
]
vkeys[v]
vkeys[v],这条边的贡献就是
v
k
e
y
s
[
s
o
n
]
×
d
i
s
(
f
a
,
s
o
n
)
×
(
K
−
v
k
e
y
s
[
s
o
n
]
)
vkeys[son]\times dis(fa,son)\times(K-vkeys[son])
vkeys[son]×dis(fa,son)×(K−vkeys[son]),所有边的贡献总和就是答案。
对于最大值,与树形
d
p
dp
dp求树的直径的方法类似,记
m
x
[
v
]
mx[v]
mx[v]为
v
v
v向下的子树中距离
v
v
v最远的点与
v
v
v之间的距离,因为虚树上所有的叶节点都是关键点,所以最大值其实就是虚树的直径。
对于最小值,可以对求最大值的方法稍作修改来得到,记
m
i
[
v
]
mi[v]
mi[v]为
v
v
v到其向下的子树中距离
v
v
v最远的关键点到
v
v
v的距离,显然所有的关键点的
m
i
[
]
mi[]
mi[]值一开始应该初始化为
0
0
0,其余的初始化为
i
n
f
inf
inf,之后完全按照与求最大值时一样的方法更新就可以了。(因为初始化的关系,从一个关键点出发的仅在一条链上的路径是不会更新答案的,因为此时
m
i
[
f
a
]
=
i
n
f
mi[fa]=inf
mi[fa]=inf,而从关键点出发的就可以更新因为此时
m
i
[
f
a
]
=
0
mi[fa]=0
mi[fa]=0,然后由于第一个儿子更新了
m
i
[
f
a
]
mi[fa]
mi[fa],所以之后在不是关键点的
f
a
fa
fa处跨两条链的距离都会更新答案,于是我们可以得出正确的最小值。
代码:
#include<bits/stdc++.h>
#include<unordered_map>
#include<unordered_set>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
#define all(x) x.begin(), x.end()
//#define int LL
#define endl '\n'
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#pragma warning(disable :4996)
const double eps = 1e-8;
const LL mod = 1000000007;
const LL MOD = 998244353;
const int maxn = 1000010;
const int maxlogn = 20;
vector<int>G[maxn];
bool used[maxn], iskey[maxn];
int N, Q, K, tot = 0, root = 1;
int mi[maxn], mx[maxn];
int H[maxn], in[maxn], out[maxn], depth[maxn], dp[maxn], vkeys[maxn], parent[maxlogn][maxn];
bool cmp(const int& a, const int& b)
{
int x = (a > 0 ? in[a] : out[-a]), y = (b > 0 ? in[b] : out[-b]);
return x < y;
}
void add_edge(int from, int to)
{
G[from].push_back(to);
G[to].push_back(from);
}
void dfs(int v, int p, int d)
{
parent[0][v] = p, depth[v] = d, in[v] = ++tot;
for (int i = 0; i < G[v].size(); i++)
{
int to = G[v][i];
if (to != p)
dfs(to, v, d + 1);
}
out[v] = ++tot;
}
void lca_init(int V)
{
dfs(root, 0, 0);
for (int k = 0; k + 1 < maxlogn; k++)
{
for (int v = 1; v <= V; v++)
{
if (parent[k][v] <= 0)
parent[k + 1][v] = 0;
else
parent[k + 1][v] = parent[k][parent[k][v]];
}
}
}
int lca(int u, int v)
{
if (depth[u] > depth[v])
swap(u, v);
for (int k = 0; k < maxlogn; k++)
{
if ((depth[v] - depth[u]) >> k & 1)
v = parent[k][v];
}
if (u == v)
return u;
for (int k = maxlogn - 1; k >= 0; k--)
{
if (parent[k][u] != parent[k][v])
{
u = parent[k][u];
v = parent[k][v];
}
}
return parent[0][u];
}
void solve()
{
vector<int>S;
stack<int>stk;
int mians = inf, mxans = -inf;
LL ans = 0;
sort(H + 1, H + K + 1, cmp);
for (int i = 1; i < K; i++)
{
int v = lca(H[i], H[i + 1]);
if (!used[v])
{
S.push_back(v), S.push_back(-v);
used[v] = true;
}
}
for (int i = 1; i <= K; i++)
S.push_back(H[i]), S.push_back(-H[i]);
sort(all(S), cmp);
int vroot = S[0];
for (auto& v : S)
{
if (v > 0)
stk.push(v);
else
{
int now = -v;
stk.pop();
if (now != vroot)
{
int fa = stk.top();
int dis = depth[now] - depth[fa];
vkeys[fa] += vkeys[now];
ans += (LL)dis * (LL)vkeys[now] * (LL)(K - vkeys[now]);
mxans = max(mxans, mx[fa] + mx[now] + dis);
mx[fa] = max(mx[fa], mx[now] + dis);
mians = min(mians, mi[fa] + mi[now] + dis);
mi[fa] = min(mi[fa], mi[now] + dis);
}
else
cout << ans << " " << mians << " " << mxans << endl;
used[now] = iskey[now] = false;
vkeys[now] = 0, mi[now] = inf, mx[now] = 0;
}
}
}
int main()
{
IOS;
cin >> N;
int u, v;
for (int i = 1; i < N; i++)
{
cin >> u >> v;
add_edge(u, v);
}
memset(mi, inf, sizeof(mi));
lca_init(N);
cin >> Q;
for (int i = 1; i <= Q; i++)
{
cin >> K;
for (int j = 1; j <= K; j++)
cin >> H[j], iskey[H[j]] = used[H[j]] = true, vkeys[H[j]] = 1, mi[H[j]] = 0;
solve();
}
return 0;
}
AHUACM寒假集训I(基础数据结构+串串)的更多相关文章
- AHUACM寒假集训VI(网络流)
luoguP2472.蜥蜴 传送门 题目大意: R × C ( 1 ≤ R , C ≤ 20 ) R\times C(1\leq R,C\leq20) R×C(1≤R,C≤20)的网格上,每个格子有一 ...
- AHUACM寒假集训II(线段树)
B.Mayor's posters POJ2528 题目大意: D.Count Color POJ2777 题目大意:长为 L ( L ≤ 1 0 5 ) L( L\leq10^5) L(L≤105) ...
- 【UOJ#228】基础数据结构练习题 线段树
#228. 基础数据结构练习题 题目链接:http://uoj.ac/problem/228 Solution 这题由于有区间+操作,所以和花神还是不一样的. 花神那道题,我们可以考虑每个数最多开根几 ...
- 理解 OpenStack + Ceph (4):Ceph 的基础数据结构 [Pool, Image, Snapshot, Clone]
本系列文章会深入研究 Ceph 以及 Ceph 和 OpenStack 的集成: (1)安装和部署 (2)Ceph RBD 接口和工具 (3)Ceph 物理和逻辑结构 (4)Ceph 的基础数据结构 ...
- hrbustoj 1551:基础数据结构——字符串2 病毒II(字符串匹配,BM算法练习)
基础数据结构——字符串2 病毒IITime Limit: 1000 MS Memory Limit: 10240 KTotal Submit: 284(138 users) Total Accepte ...
- hrbustoj 1545:基础数据结构——顺序表(2)(数据结构,顺序表的实现及基本操作,入门题)
基础数据结构——顺序表(2) Time Limit: 1000 MS Memory Limit: 10240 K Total Submit: 355(143 users) Total Accep ...
- 关于SparkMLlib的基础数据结构 Spark-MLlib-Basics
此部分主要关于MLlib的基础数据结构 1.本地向量 MLlib的本地向量主要分为两种,DenseVector和SparseVector,顾名思义,前者是用来保存稠密向量,后者是用来保存稀疏向量,其创 ...
- Vlc基础数据结构记录
1. Vlc基础数据结构 hongxianzhao@hotmail.com 1.1 基础数据结构 struct vlc_object_t,相关文件为src\misc\objects.c. 定义为: ...
- 基础数据结构之(Binary Trees)
从头开始刷ACM,真的发现过去的很多漏洞,特别越是基础的数据结构,越应该学习得精,无论是ACM竞赛,研究生考试,还是工程上,对这些基础数据结构的应用都非常多,深刻理解非常必要.不得不说最近感触还是比较 ...
随机推荐
- collate utf8_bin是什么意思
创建数据库时 collate utf_bin是 以二进制值比较,也就是区分大小写,collate是核对的意思 uft-8_general_ci 一般比较,不区分大小写
- 裸k8s搭建中遇到的两个坑
在装docker的时候报错了,需要先安装selinux版本.才能安装容器. 需要按照提示安装这个包. 采用强制安装.rpm -ivh 包名字 --force --nodeps 在k8s的master上 ...
- MySQL 5.7主从搭建(同一台机器)
主从复制原理:复制是 MySQL 的一项功能,允许服务器将更改从一个实例复制到另一个实例. 1)主服务器将所有数据和结构更改记录到二进制日志中. 2)从属服务器从主服务器请求该二进制日志并在本地应用其 ...
- [JavaWeb]Log4j的前因后果
Log4j的前因后果 简介 Log4j的进化史 Log4J的三大组件: Logger:日志记录器,负责收集处理日志记录 (如何处理日志) Appender:日志输出目的地,负责日志的输出 (输出到什么 ...
- Gulp自动化任务及nvm、npm常用命令
项目环境配置 nvm: node版本管理工具,安装和环境变量 cmd常用命令: · nvm use [version]: 切换至指定版本的node · nvm install no ...
- Notepad++官网地址 https://notepad-plus-plus.org/
Notepad++官网地址 https://notepad-plus-plus.org/
- Linux-一次执行多个命令 ; && ||
一次执行多个命令,多个命令之间用:号隔开 cmd1;cmd2:cmd3 这样前后执行的时候没有依赖性,如果有下列要求呢 1. cmd1执行失败那就不要执行后面的命令 2. cmd1失败了才去指令后面的 ...
- 关于synchronized(this)中this指的是什么意思
public class SynchronizedDEmo { public static void main(String[] args) { TestThread tt = new TestThr ...
- 人工智能与智能系统3-> 机器人学3 | 移动机器人平台
机器人学的基本工具已经了解完毕,现在开始了解移动机器人,这部分包括机器人平台.导航.定位. 所谓机器人平台就是指机器人的物理结构及其驱动方式.本文将学习两种典型移动机器人平台(四旋翼和轮式车)的运动与 ...
- 理解ASP.NET Core - 基于JwtBearer的身份认证(Authentication)
注:本文隶属于<理解ASP.NET Core>系列文章,请查看置顶博客或点击此处查看全文目录 在开始之前,如果你还不了解基于Cookie的身份认证,那么建议你先阅读<基于Cookie ...
