leetcode 有效三角形的个数

题目描述：

平明伞兵解法：

既然要求满足三角形要求的三边，简单来说，就是最短两边之和大于第三边，所以，第一步Arrays.sort()。先排序，然后直接伞兵暴力法，三重循环。当然最后肯定是能跑出来的，但是复杂度之大。

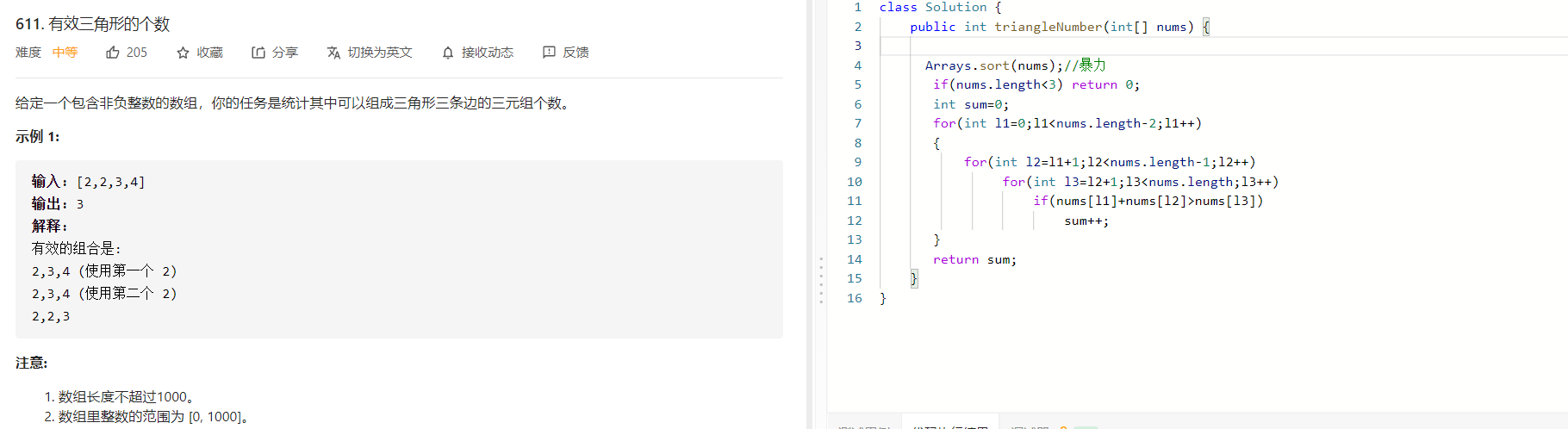
 思考后的解法:

其实在写暴力的时候，就应该心理有数，我们其实做了许多大量的重复工作，所以可以用排序后的二分查找，以及双指针进行操作。

方法二：二分查找

首先对数组排序。

固定最短的两条边，二分查找最后一个小于两边之和的位置。可以求得固定两条边长之和满足条件的结果。枚举结束后，总和就是答案。

时间复杂度为 O(n^2logn)。

方法三：双指针

首先对数组排序。

固定最长的一条边，运用双指针扫描

如果 nums[l] + nums[r] > nums[i]，同时说明 nums[l + 1] + nums[r] > nums[i], ..., nums[r - 1] + nums[r] > nums[i]，满足的条件的有 r - l 种，r 左移进入下一轮。

如果 nums[l] + nums[r] <= nums[i]，l 右移进入下一轮。

枚举结束后，总和就是答案。

时间复杂度为 O(n^2)

作者：jerring

链接：https://leetcode-cn.com/problems/valid-triangle-number/solution/ming-que-tiao-jian-jin-xing-qiu-jie-by-jerring/

来源：力扣（LeetCode）

方法二：二分查找
首先对数组排序。固定最短的两条边，二分查找最后一个小于两边之和的位置。可以求得固定两条边长之和满足条件的结果。枚举结束后，总和就是答案。时间复杂度为 O(n^2logn)O(n 2 logn)。Java
class Solution {    public int triangleNumber(int[] nums) {        Arrays.sort(nums);        int n = nums.length;        int res = 0;        for (int i = 0; i < n - 2; ++i) {            for (int j = i + 1; j < n - 1; ++j) {                int s = nums[i] + nums[j];                int l = j + 1, r = n - 1;                while (l < r) {                    int mid = l + r + 1 >>> 1;                    if (nums[mid] < s) l = mid;                    else r = mid - 1;                }                if (nums[r] < s) {                    res += r - j;                }            }        }        return res;    }}方法三：双指针
首先对数组排序。固定最长的一条边，运用双指针扫描如果 nums[l] + nums[r] > nums[i]，同时说明 nums[l + 1] + nums[r] > nums[i], ..., nums[r - 1] + nums[r] > nums[i]，满足的条件的有 r - l 种，r 左移进入下一轮。如果 nums[l] + nums[r] <= nums[i]，l 右移进入下一轮。枚举结束后，总和就是答案。时间复杂度为 O(n^2)O(n 2 )。Java
class Solution {    public int triangleNumber(int[] nums) {        Arrays.sort(nums);        int n = nums.length;        int res = 0;        for (int i = n - 1; i >= 2; --i) {            int l = 0, r = i - 1;            while (l < r) {                if (nums[l] + nums[r] > nums[i]) {                    res += r - l;                    --r;                } else {                    ++l;                }            }        }        return res;    }}
作者：jerring链接：https://leetcode-cn.com/problems/valid-triangle-number/solution/ming-que-tiao-jian-jin-xing-qiu-jie-by-jerring/来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。