The Expressive Power of Neural Networks: A View from the Width

概
主要内容
- 定理1
- 定理2
- 定理3
- 定理4
- 定理1的证明

Lu Z, Pu H, Wang F, et al. The expressive power of neural networks: a view from the width[C]. neural information processing systems, 2017: 6232-6240.

@article{lu2017the,

title={The expressive power of neural networks: a view from the width},

author={Lu, Zhou and Pu, Hongming and Wang, Feicheng and Hu, Zhiqiang and Wang, Liwei},

pages={6232--6240},

year={2017}}

概

Universal approximation theorem-wiki, 这个定理分成俩个部分, 第一个部分是Unbounded Width Case, 这篇文章是Bounded Width Case (ReLu网络).

主要内容

定理1

另外, 定理1中的网络由若干个(视\(\epsilon\)而定) blocks排列而成, 每个block具有以下性质:

depth: 4n+1, width: n+4 的神经网络
在一个范围外其“函数值”为0
它能够存储样本信息
它会加总自身的信息和前面的逼近信息

定理2

定理3

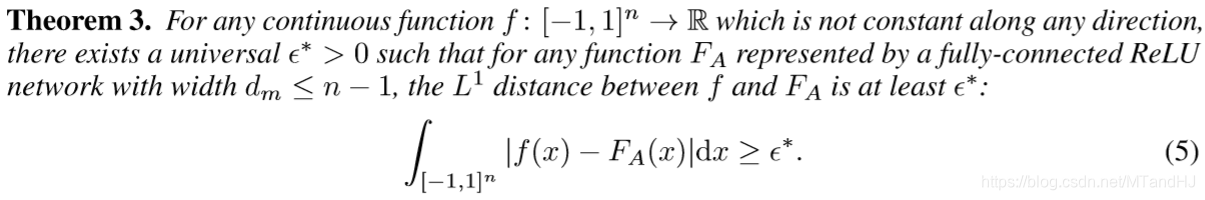
定理4

定理1的证明

因为主要关注定理1, 所以讲下这个部分的证明(实际上是因为其它懒得看了).

假设\(x = (x_1, x_2,\ldots, x_n)\)为输入, \(f\)是\(L^1\)可积的, 对于任意的\(\epsilon > 0\), 存在\(N > 0\)满足

\[\int_{\cup_{i=1}^n|x_i| \ge N} |f| \mathrm{d}x < \frac{\epsilon}{2}.
\]

定义下列符号:

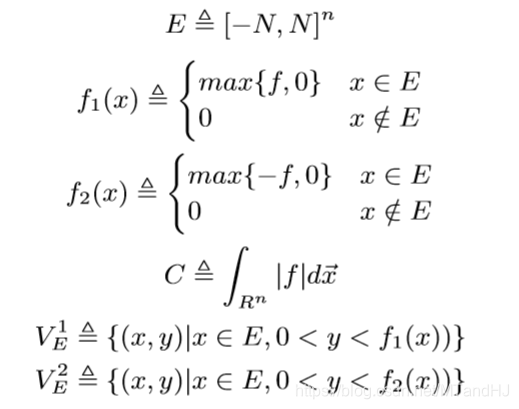
则我们有:

\[\int_{R^n} |f-(f_1 - f_2)| \mathrm{d}x < \frac{\epsilon}{2},
\]

对于\(i=1, 2\), 既然\(V_E^i\)是可测的(且测度小于\(+\infty\)), 则我们能找到有限个\(n+1\)维的矩体去逼近(原文用了cover, 但是我感觉这里用互不相交的矩体才合理), 并有

\[m(V_E^i \Delta \cup_j J_{j,i}) < \frac{\epsilon}{8},
\]

不出意外\(\Delta\)应该就是\.

假设\(J_{j,i}\)有\(n_i\)个, 且

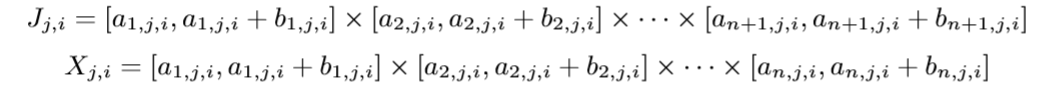
每一个\(J_{j, i}\)对应一个指示函数:

\[\phi_{j,i}(x) = \left \{
\begin{array}{ll}
1 & x \in X_{j,i} \\
0 & x \not \in X_{j,i}.
\end{array} \right.
\]

则

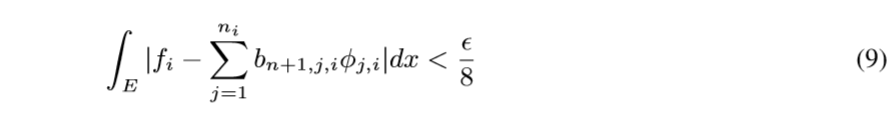
这个在实变函数将多重积分, 提到的下方图形集有讲到.

于是我们有(\(-f_1-f_2+f_1+f_2-f+f\)然后拆开来就可以得到不等式)

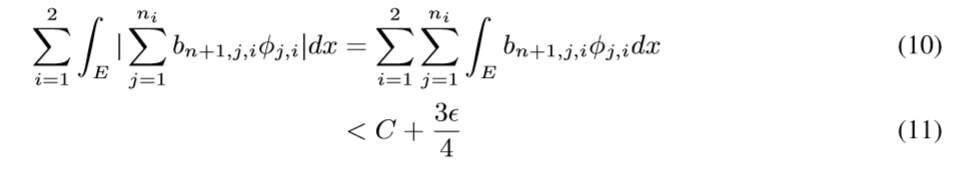
现在我们要做的就是通过神经网络拟合\(\varphi_{j,i}\)去逼近\(\phi_{j,i}\), 使得

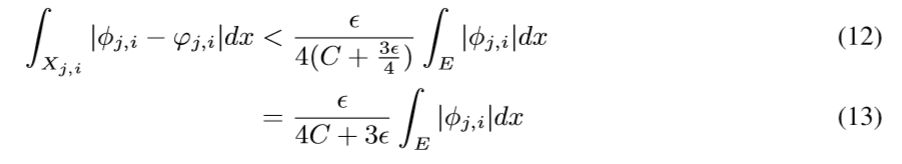
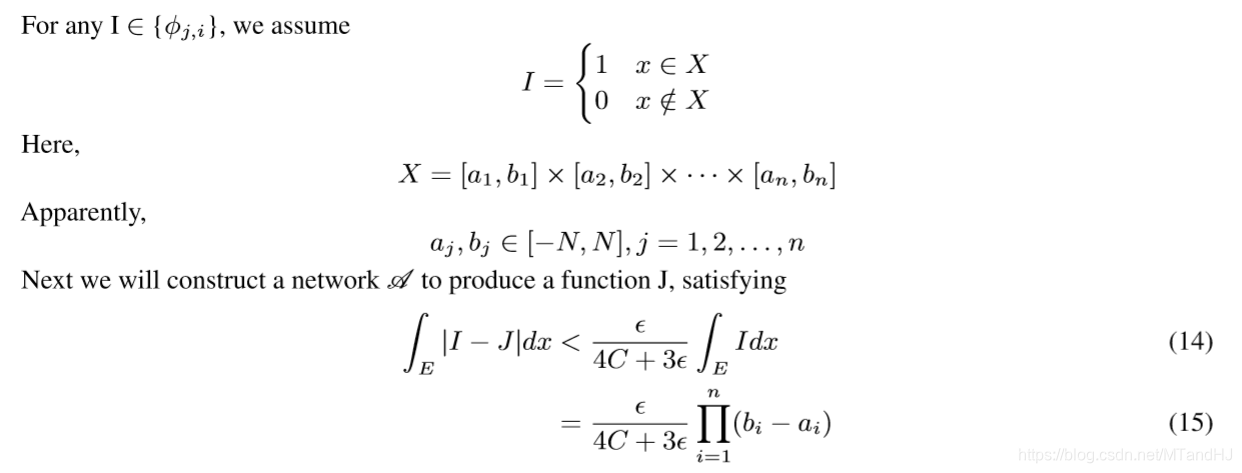
现在来讲, 如果构造这个神经网络:

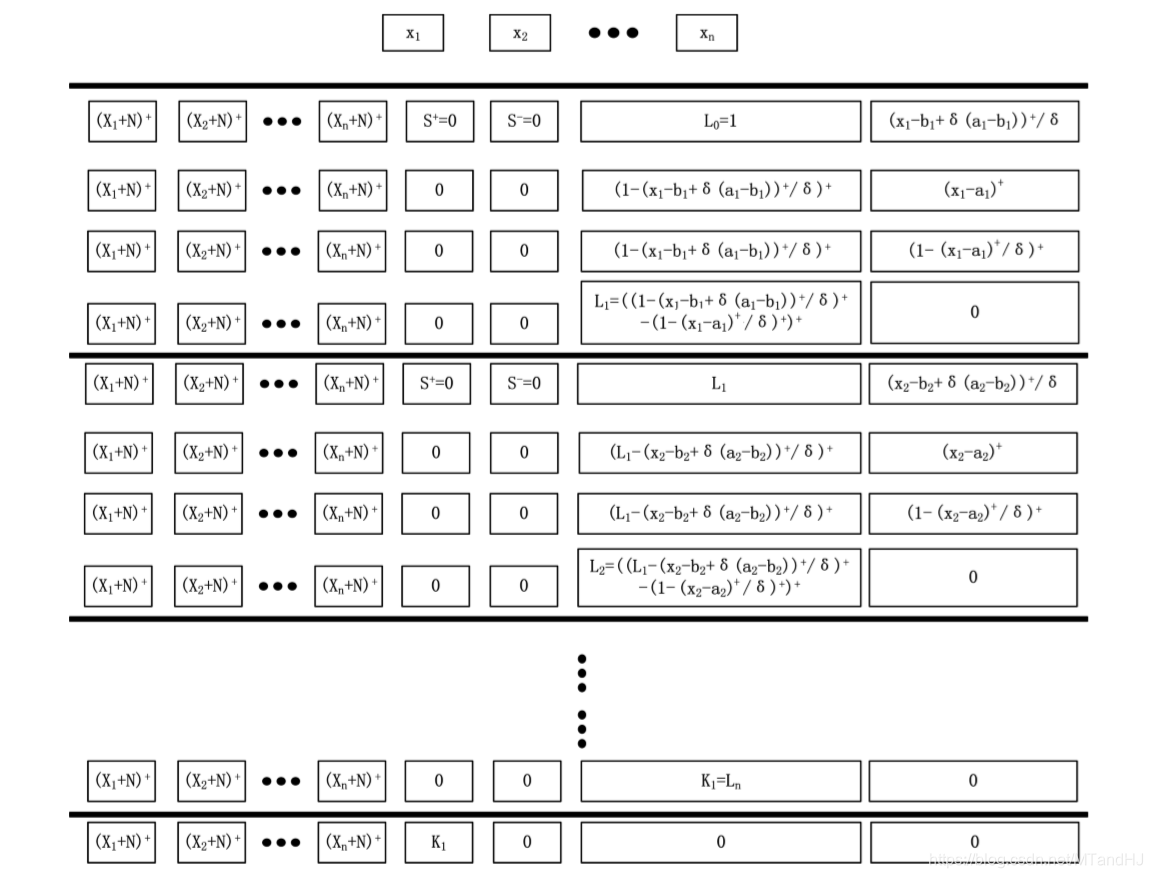
一个block有4n+1层, 每层的width是n+4, 注意到所有层的前n个Node都是一样的用来保存样本信息. 我们用\(R_{i, j, \mathscr{B_k}}, i=1, 2, 3, 4, j=1,\ldots,n+4, k=1,\ldots, n,\) 表示第\(k\)个Unit(每个Unit有4层)的第\(i\)层的第\(j\)个Node.

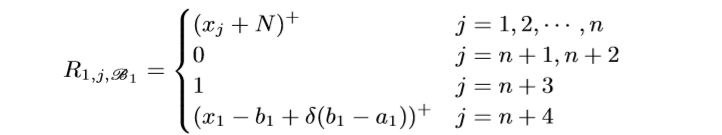
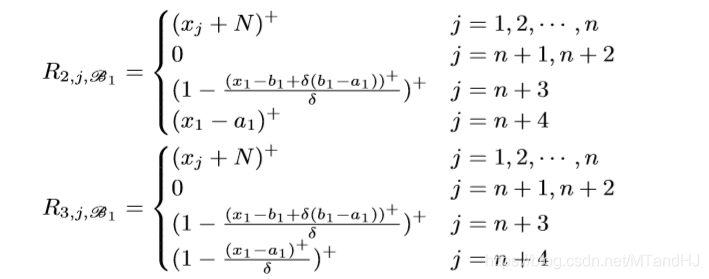
注意: \(R_{2, n+3, \mathscr{B_1}}\)应该是\((x_1-a_1)^+/\delta\), 最开始的结构图中的对的. 我们来看一下, 什么样的\(x=(x_1, \ldots, x_n)\), 会使得\(L_1\)不为0.

如果\(x_1=a_1+\delta(b_1-a_1)+\epsilon\), 这里\(\epsilon>0\)是一个任意小量, 和上文中的\(\epsilon\)没有关系. 此时(当\(\delta<1/2\))

\[\frac{(x_1-b_1+\delta(b_1-a_1))^+}{\delta}= 0,
\]

当\(\delta\)足够小的时候

\[\frac{(x_1-a_1)^+}{\delta}= 0，
\]

此时\(L_1=1\), 类似地, 可以证明, 当\(\delta \rightarrow 0\)的时候, \(x_1 \in (a_1+\delta(b_1-a_1),b_1-\delta(b_1-a_1))\)时, \(L_1=1\), 否则为0.

\(R_{i, j, \mathscr{B_k}}\)的定义是类似的, 只是

\[L_k = ((L_{k-1}-(x_k-b_k+\delta(a_k-b_k))^+/\delta)^+- (1-(x_k-a_k)^+/\delta)^+)^+,
\]

可以证明, 当\(\delta\rightarrow 0\), 且\(x_t \in (a_t + \delta(b_t-a_t),b_t-\delta(b_t-a_t)), t=1,2,\ldots, k\)的时候, \(L_k=1.\), 这样我们就构造了一个指示函数, 如果这个这函数对应的\(i\)为1则将\(L_n\)存入n+1 Node, 否则 n+2 Node (实际上, 我感觉应该存的是\(b_{n+1,j,i}L_n\)), 则

这里\(\mu\)相当于\(L_n\). 所以多个blocks串联起来后, 我们就得到了一个函数, 且这个函数是我们想要的.

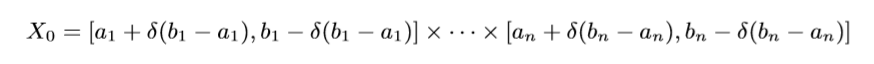
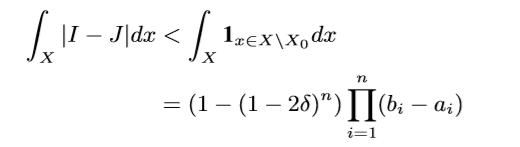
这个直接通过超距体体积计算得来的, 我们只需要取:

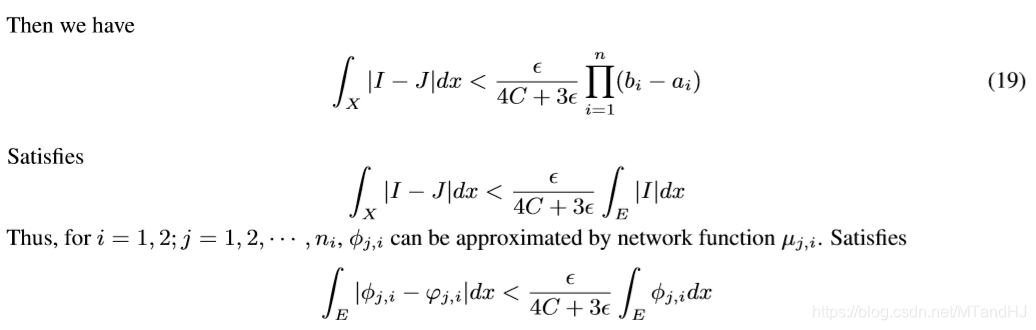
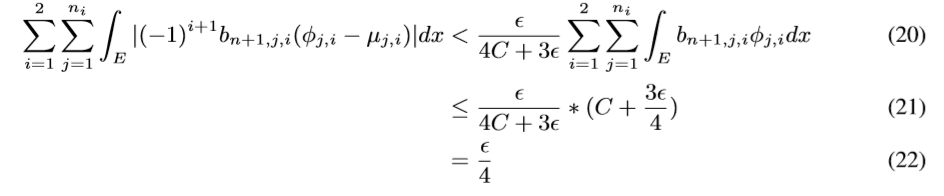
最后

令\(g:=\sum_{i=1}^2\sum_{j=1}^{n_i}(-1)^{i+1}b_{n+1,j,i}\mu_{j,i}\)，便有

此即定理1的证明.