2021.10.11考试总结[NOIP模拟74]

T1 自然数

发现\(mex\)是单调不降的，很自然地想到用线段树维护区间端点的贡献。

枚举左端点，用线段树维护每个右端点形成区间的\(mex\)值。每次左端点右移相当于删去一个数。

记\(a_i\)在\(i\)下一次出现的位置为\(pos_i\)，那么左端点\(i\)移到\(i+1\)，实际上就是将左端点在\([i,pos_i)\)的区间中\(mex\)值大于\(a_i\)的改为\(a_i\)。线段树上二分可以解决，中途要记区间最小值便于二分。

\(code:\)

T1

#include<bits/stdc++.h>
#define int long long
using namespace std;

namespace IO{
	typedef long long LL;
	auto read=[]()->int{
		char ch=getchar(); int x=0,f=1;
		while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
		while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
		return x*f;
	};
	auto write=[](LL x,int sp)->void{
		char ch[20]; int len=0;
		if(x<0){ x=~x+1; putchar('-'); }
		do{ ch[len++]=(1<<4)+(1<<5)+x%10; x/=10; }while(x);
		for(int i=len-1;~i;--i) putchar(ch[i]); putchar(sp);
	};
	auto ckmax=[](int& x,int y)->void{ x=x<y?y:x; };
	auto ckmin=[](int& x,int y)->void{ x=x<y?x:y; };
} using namespace IO;

const int NN=200010;
int n,ans,tmp,a[NN];
vector<int>loc[NN];
bool bin[NN];

namespace segment_tree{
	#define ld rt<<1
	#define rd (rt<<1)|1
	int sum[NN<<2],mnn[NN<<2],tag[NN<<2],len[NN<<2];
	void pushup(int rt){
		sum[rt]=sum[ld]+sum[rd];
		mnn[rt]=min(mnn[ld],mnn[rd]);
	}
	void pushdown(int rt){
		if(tag[rt]<0) return;
		sum[ld]=tag[rt]*len[ld];
		sum[rd]=tag[rt]*len[rd];
		mnn[ld]=mnn[rd]=tag[rt];
		tag[ld]=tag[rd]=tag[rt];
		tag[rt]=-1;
	}
	void build(int rt,int l,int r){
		len[rt]=r-l+1; tag[rt]=-1;
		if(l==r) return;
		int mid=l+r>>1;
		build(ld,l,mid);
		build(rd,mid+1,r);
	}
	void insert(int rt,int l,int r,int pos,int val){
		if(l==r) return sum[rt]=mnn[rt]=val,void();
		int mid=l+r>>1;
		if(pos<=mid) insert(ld,l,mid,pos,val);
		else insert(rd,mid+1,r,pos,val);
		pushup(rt);
	}
	void modify(int rt,int l,int r,int opl,int opr,int val){
		if(l==r){
			if(mnn[rt]>val) mnn[rt]=sum[rt]=val;
			return;
		}
		pushdown(rt);
		int mid=l+r>>1;
		if(l>=opl&&r<=opr){
			if(mnn[rt]>=val){
				mnn[rt]=tag[rt]=val;
				sum[rt]=val*len[rt];
			} else if(mnn[rd]>=val){
				mnn[rd]=tag[rd]=val;
				sum[rd]=val*len[rd];
				modify(ld,l,mid,opl,opr,val);
				pushup(rt);
			} else modify(rd,mid+1,r,opl,opr,val),pushup(rt);
			return;
		}
		if(opl<=mid) modify(ld,l,mid,opl,opr,val);
		if(opr>mid) modify(rd,mid+1,r,opl,opr,val);
		pushup(rt);
	}
	int query(int rt,int l,int r,int opl,int opr){
		if(l>=opl&&r<=opr) return sum[rt];
		pushdown(rt);
		int mid=l+r>>1,res=0;
		if(opl<=mid) res+=query(ld,l,mid,opl,opr);
		if(opr>mid) res+=query(rd,mid+1,r,opl,opr);
		return res;
	}
} using namespace segment_tree;

signed main(){
	freopen("mex.in","r",stdin);
	freopen("mex.out","w",stdout);
	n=read(); build(1,1,n);
	for(int i=1;i<=n;i++){
		a[i]=read();
		if(a[i]<=n)
			loc[a[i]].push_back(i), bin[a[i]]=1;
		while(bin[tmp]) ++tmp;
		insert(1,1,n,i,tmp);
	}
	for(int i=0;i<=n;i++)
		if(loc[i].size())
			loc[i].push_back(n+1);
	for(int i=1;i<=n;i++){
		ans+=query(1,1,n,i,n);
		if(a[i]>n) continue;
		int pos=*upper_bound(loc[a[i]].begin(),loc[a[i]].end(),i);
		modify(1,1,n,i,pos-1,a[i]);
	}
	return write(ans,'\n'),0;
}

T2 钱仓

对于正整数\(a,b\)，\(a^2+b^2<(a+b)^2\)。于是有贪心：断环为链后从后往前扫，每次遇到有东西的仓库，就把东西移到最靠后的位置。

发现不管怎么贪心，最后都是最优解。于是找到一个合法端点贪心一遍即可。

\(code:\)

T2

#include<bits/stdc++.h>
#define int long long
using namespace std;

namespace IO{
	auto read=[]()->int{
		char ch=getchar(); int x=0,f=1;
		while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
		while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
		return x*f;
	};
	auto write=[](int x,int sp)->void{
		char ch[20]; int len=0;
		if(x<0){ x=~x+1; putchar('-'); }
		do{ ch[len++]=(1<<4)+(1<<5)+x%10; x/=10; }while(x);
		for(int i=len-1;~i;--i) putchar(ch[i]); putchar(sp);
	};
	auto ckmax=[](int& x,int y)->void{ x=x<y?y:x; };
	auto ckmin=[](int& x,int y)->void{ x=x<y?x:y; };
} using namespace IO;

const int NN=100010;
int n,s,mx,pre,res,c[NN<<1],o[NN];
int calc(int x){ return x*(x+1)*(2*x+1)/6; }

signed main(){
	freopen("barn.in","r",stdin);
	freopen("barn.out","w",stdout);
	n=read();
	for(int i=1;i<=n;i++) c[i]=c[i+n]=read();
	for(int i=1;i<=n;i++){
		pre+=c[i]-1;
		if(pre<0) s=i+1,pre=0;
	} pre=0;
	for(int i=s+n-1;i>=s;i--){
		if(!c[i]){ if(!pre) pre=i; }
		else if(pre) res+=calc(pre-i)-calc(pre-i-c[i]),pre-=c[i];
	}
	return write(res,'\n'),0;
}
/*
10
1
0
0
2
0
0
1
2
2
2

*/

T3 游戏

令\(Alice\)为\(A\)，\(Bob\)为\(B\)，设\(a_n\)，\(b_n\)分别为\(A\)，\(B\)在剩\(n\)个石子时先手，\(A\)的胜率。

一些结论：

• 若A先手，A认为现在想投某一面更优，那么在当前这个石子被某一个人拿走之前她会一直想投这一面，B先手时对于B也是如此
• 若A先手，为了阻止A投到某一面，B也要选择投这一面，也就是说对于任意一个石子，A和B的决策相同

不难推出转移式子：

若\(a_n\geq b_n\):

\[a_{n+1}=(1-p)\times b_n+p\times(1-q)\times a_n+p\times q\times a_{n+1}
\]

\[a_{n+1}=\frac{p\times(1-q)\times a_n+(1-p)\times b_n}{1-p\times q}
\]

同理，

\[b_{n+1}=(1-q)\times a_n+q\times(1-p)\times b_n+p\times q\times b_{n+1}
\]

\[b_{n+1}=\frac{(1-q)\times a_n+q\times(1-p)\times b_n}{q-p\times q}
\]

\(a_n\leq b_n\)时类似，

\[a_{n+1}=\frac{q\times(1-p)\times a_n+p\times b_n}{p+q-p\times q}
\]

\[b_{n+1}=\frac{q\times a_n+p\times(1-q)\times b_n}{p+q-p\times q}
\]

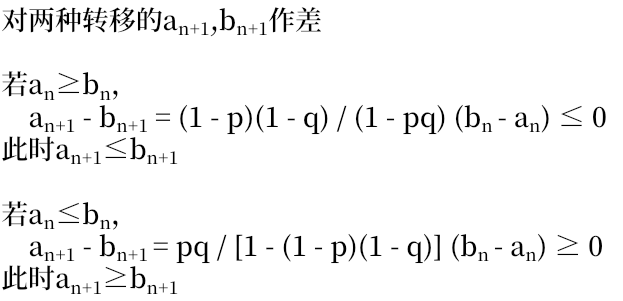
实际上就是\(n\)为奇数时用第一种转移，为偶数时用第二种转移。将奇偶转移合为一次转移，矩阵优化。

\(code:\)

T3

#include<bits/stdc++.h>
#define int long long
using namespace std;

namespace IO{
	auto read=[]()->int{
		char ch=getchar(); int x=0,f=1;
		while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
		while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
		return x*f;
	};
	auto write=[](int x,int sp)->void{
		char ch[20]; int len=0;
		if(x<0){ x=~x+1; putchar('-'); }
		do{ ch[len++]=(1<<4)+(1<<5)+x%10; x/=10; }while(x);
		for(int i=len-1;~i;--i) putchar(ch[i]); putchar(sp);
	};
	auto ckmax=[](int& x,int y)->void{ x=x<y?y:x; };
	auto ckmin=[](int& x,int y)->void{ x=x<y?x:y; };
} using namespace IO;

const int mod=1e9+7;
int T,n,p,q;
int qpow(int a,int b){
	int res=1; a%=mod;
	for(;b;b>>=1){
		if(b&1) res=res*a%mod;
		a=a*a%mod;
	}
	return res;
}
const int inv=qpow(100000000,mod-2),inv3=qpow(3,mod-2);

namespace Matrix{
	struct mat{
		int s[3][3];
		mat(){}
		mat(int x){ memset(s,0,sizeof(s)); s[1][1]=s[2][2]=x; }
		mat operator*(const mat& a)const{
			mat res=mat(0);
			for(int i=1;i<3;i++)
				for(int k=1;k<3;k++)
					for(int j=1;j<3;j++)
						(res.s[i][j]+=s[i][k]*a.s[k][j])%=mod;
			return res;
		}
	}s,t,t1,t2;
	mat operator^(mat a,int b){
		mat res=mat(1);
		for(;b;b>>=1){
			if(b&1) res=res*a;
			a=a*a;
		}
		return res;
	}
	void prework(){
		s.s[1][2]=1; s.s[1][1]=0;
		t1.s[1][1]=(mod+1-p)*q%mod*qpow(mod+p+q-p*q%mod,mod-2)%mod;
		t1.s[2][1]=p*qpow(mod+p+q-p*q%mod,mod-2)%mod;
		t1.s[1][2]=q*qpow(mod+p+q-p*q%mod,mod-2)%mod;
		t1.s[2][2]=(mod+1-q)*p%mod*qpow(mod+p+q-p*q%mod,mod-2)%mod;
		t2.s[1][1]=p*(mod+1-q)%mod*qpow(mod+1-p*q%mod,mod-2)%mod;
		t2.s[2][1]=(mod+1-p)*qpow(mod+1-p*q%mod,mod-2)%mod;
		t2.s[1][2]=(mod+1-q)*qpow(mod+1-p*q%mod,mod-2)%mod;
		t2.s[2][2]=q*(mod+1-p)%mod*qpow(mod+1-p*q%mod,mod-2)%mod;
		t=t1*t2;
	}
} using namespace Matrix;

signed main(){
	freopen("game.in","r",stdin);
	freopen("game.out","w",stdout);
	T=read();
	while(T--){
		n=read(); p=read(); q=read();
		p=p*inv%mod; q=q*inv%mod;
		prework();
		t=t^(n/2); s=s*t;
		if(n&1) s=s*t1;
		write(s.s[1][1],'\n');
	}
	return 0;
}