Codeforces 587D - Duff in Mafia（2-SAT+前后缀优化建图）

Codeforces 题面传送门 & 洛谷题面传送门

2-SAT hot tea。

首先一眼二分答案，我们二分答案 \(mid\)，那么问题转化为，是否存在一个所有边权都 \(\le mid\) 的集合 \(S\)，满足 \(S\)​ 中任意两条边的端点互不相同，并且没有选择的选择的边每种颜色的边两两之间的端点也互不相同。

乍一看这个问题看似无法解决。但不难发现每条边只有两种状态——选或不选，也就是说我们考虑将每条边拆成两个点 \(x_i\)​ 和 \(\lnot x_i\)​，分别表示边 \(i\)​ 被选入集合 \(S\)​ 中和边 \(i\)​ 没有被选入集合 \(S\) 然后跑 2-SAT​，那么考虑这样建图：

• 对于权值 \(>mid\)​ 的边我们连一条 \(x_i\to\lnot x_i\) 的边，这样只要选择了 \(x_i\) 就必定会推出 \(\lnot x_i\) 也为真，也就导致了矛盾，因此这样连边就强制要求 \(\lnot x_i\) 必须为真。
• 对于两条有公共端点的边 \(i,j\)，如果它们同时被纳入集合 \(S\) 中就会导致 \(S\) 中的边构不成匹配，因此如果 \(x_i\) 为真必然可以推出 \(\lnot x_j\) 为真，因此我们考虑连边 \(x_i\to\lnot x_j\)，同理逆否命题 \(x_j\to\lnot x_i\)。
• 类似地，对于两条有公共端点且颜色相同的边 \(i,j\)，如果它们同时不选，就会导致没选入 \(S\) 的边不合法，因此我们连边 \(\lnot x_i\to x_j,\lnot x_j\to x_i\)

这样暴力连边复杂度是 \(\mathcal O(m^2)\) 的，无法通过，考虑优化。以第二类边为例，我们考虑枚举两条边的公共点 \(i\)​，那么我们考虑将所有与 \(i\) 相连的边排成一列，设为 \(e_1,e_2,\cdots,e_k\)，那么我们需要对于所有 \(1\le p,q\le k,p\ne q\)，连边 \(x_p\to\lnot x_q\)，不难发现这可以用前后缀优化建图优化，具体优化方案如下：

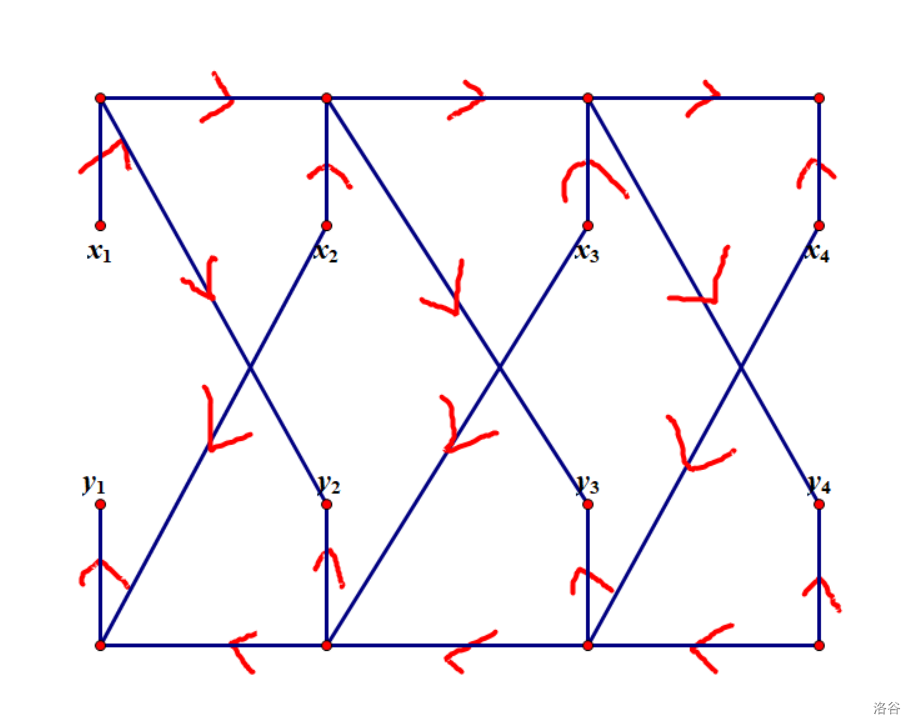
对于第三类边也按照同样方式优化一下即可。这样边数即可降到 \(\mathcal O(m)\) 级别。然后跑 tarjan，如果发现 \(\exists i\)，\(x_i\) 与 \(\lnot x_i\) 在同一个强连通分量中说明 \(mid\) 不合法，否则由于 tarjan 强连通分量编号按照缩点后拓扑序，可通过 \(x_i\) 与 \(\lnot x_i\) 所在强连通分量大小关系判断 \(i\) 是否被选入集合 \(S\)。

时间复杂度 \(\mathcal O((n+m)\log n)\)，为了减少常数可先把二、三类边建出来并保存一个备份，这样每次 check 时只需建一类边即可，不必每次二分都把整张图重新建出来。

const int MAXN=5e4;
const int MAXM=5e4;
const int MAXV=5e5;
const int MAXE=2e6;
int n,m,mx,ncnt=0;
struct edge{int u,v,c,t;} e[MAXM+5];
vector<int> g[MAXN+5];
vector<pii> col[MAXN+5];
int hd[MAXV+5],to[MAXE+5],nxt[MAXE+5],ec=0;
int _hd[MAXV+5],_ec=0;
void adde(int u,int v){to[++ec]=v;nxt[ec]=hd[u];hd[u]=ec;}
int dfn[MAXV+5],low[MAXV+5],stk[MAXV+5],tp=0;
int bel[MAXV+5],cmp=0,tim=0;bool vis[MAXV+5];
void tarjan(int x){
	dfn[x]=low[x]=++tim;stk[++tp]=x;vis[x]=1;
	for(int e=hd[x];e;e=nxt[e]){
		int y=to[e];
		if(!dfn[y]) tarjan(y),chkmin(low[x],low[y]);
		else if(vis[y]) chkmin(low[x],dfn[y]);
	}
	if(dfn[x]==low[x]){
		int o;cmp++;do{
			o=stk[tp--];bel[o]=cmp;vis[o]=0;
		} while(o^x);
	}
}
bool check(int mid){
	for(int i=1;i<=ncnt;i++) hd[i]=_hd[i];ec=_ec;
	memset(dfn,0,sizeof(dfn));memset(low,0,sizeof(low));tim=cmp=tp=0;
	for(int i=1;i<=m;i++) if(e[i].t>mid) adde(i,i+m);
	for(int i=1;i<=ncnt;i++) (!dfn[i]&&(tarjan(i),0));
	for(int i=1;i<=m;i++) if(bel[i]==bel[i+m]) return 0;
	return 1;
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d%d%d",&e[i].u,&e[i].v,&e[i].c,&e[i].t);
		chkmax(mx,e[i].t);g[e[i].u].pb(i);g[e[i].v].pb(i);
		col[e[i].u].pb(mp(e[i].c,i));col[e[i].v].pb(mp(e[i].c,i));
	} ncnt=m<<1;
	for(int i=1;i<=n;i++) sort(col[i].begin(),col[i].end());
	for(int i=1;i<=n;i++){
		vector<int> pre(g[i].size()),suf(g[i].size());
		for(int j=0;j<pre.size();j++) pre[j]=++ncnt;
		for(int j=0;j<suf.size();j++) suf[j]=++ncnt;
		for(int j=1;j<pre.size();j++) adde(pre[j-1],pre[j]);
		for(int j=1;j<suf.size();j++) adde(suf[j],suf[j-1]);
		for(int j=0;j<pre.size();j++) adde(g[i][j],pre[j]);
		for(int j=0;j<suf.size();j++) adde(suf[j],g[i][j]+m);
		for(int j=1;j<pre.size();j++) adde(pre[j-1],g[i][j]+m),adde(g[i][j],suf[j-1]);
	}
	for(int i=1;i<=n;i++){
		for(int l=0,r;l<col[i].size();l=r){
			r=l;while(r<col[i].size()&&col[i][r].fi==col[i][l].fi) ++r;
			vector<int> pre(r-l),suf(r-l);
			for(int j=0;j<pre.size();j++) pre[j]=++ncnt;
			for(int j=0;j<suf.size();j++) suf[j]=++ncnt;
			for(int j=1;j<pre.size();j++) adde(pre[j-1],pre[j]);
			for(int j=1;j<suf.size();j++) adde(suf[j],suf[j-1]);
			for(int j=0;j<pre.size();j++) adde(pre[j],col[i][j+l].se);
			for(int j=0;j<suf.size();j++) adde(col[i][j+l].se+m,suf[j]);
			for(int j=1;j<pre.size();j++) adde(col[i][j-1+l].se+m,pre[j]),adde(suf[j],col[i][j-1+l].se);
		}
	}
	for(int i=1;i<=ncnt;i++) _hd[i]=hd[i];_ec=ec;
	int l=0,r=mx,p=-1;
	while(l<=r){
		int mid=l+r>>1;
		if(check(mid)) p=mid,r=mid-1;
		else l=mid+1;
	} if(!~p) puts("No");
	else{
		printf("Yes\n%d ",p);check(p);vector<int> vec;
		for(int i=1;i<=m;i++) if(bel[i]<bel[i+m]) vec.pb(i);
		printf("%d\n",vec.size());for(int x:vec) printf("%d ",x);
	}
	return 0;
}