hdu5438 拓扑排序+DFS

解析

对一个有向无环图（Directed Acyclic Graph，简称DAG）G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若<u，v> ∈E(G)，则u在线性序列中出现在v之前。

效果如图：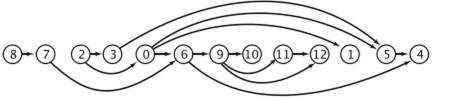

模板

void toposort(int map[MAX][MAX],int indegree[MAX],int n)
{
    int i,j,k;
    for(i=0;i<n;i++) //遍历n次
    {
        for(j=0;j<n;j++) //找出入度为0的节点
        {
            if(indegree[j]==0)
            {
                indegree[j]--;
                cout<<j<<endl;
                for(k=0;k<n;k++) //删除与该节点关联的边
                {
                    if(map[j][k]==1)
                    {
                        indegree[k]--;
                    }
                }
                break;
            }
        }
    }
}

代码

#include <bits/stdc++.h>
using namespace std;

struct Edge{
int u,v,next;
}edge[2000005];

int d[10005],head[10005],power[10005];

bool vis[10005];

int e,m,n,num;

long long sum;

void add(int a,int b)
{
    edge[e].u=a;
    edge[e].v=b;        //建立一个a-b的边
    edge[e].next=head[a];   //上一条以a为顶点的边的序号
    head[a]=e++;   //最后一条以a为顶点的边的序号
}

void dfs(int a)
{
    sum += power[a];
    num++;
    vis[a]=true;
    for(int i=head[a];i!=-1;i=edge[i].next)
    {
        if(!vis[edge[i].v]) dfs(edge[i].v);
    }
}

void topo()
{
    queue<int>q;
    for(int i=1;i<=n;i++)
    {
        if(d[i]==1) q.push(i);
    }
    while(!q.empty())
    {
        int tmp=q.front();
        q.pop();
        vis[tmp]=true;
        d[tmp]--;
        for(int i=head[tmp];i!=-1;i=edge[i].next)
        {
            int v=edge[i].v;
            if(d[v]>0) d[v]--;
            if(d[v]==1) q.push(v);
        }
    }
}

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int u,v;
        e=0;
        memset(d,0,sizeof(d));
        memset(head,-1,sizeof(head));
        memset(vis,false,sizeof(vis));
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++) scanf("%d",&power[i]);
        for(int i=1;i<=m;i++)
        {
            scanf("%d%d",&u,&v);
            d[u]++;
            d[v]++;
            add(u,v);
            add(v,u);
        }
        topo();
        long long ans=0;
        for(int i=1;i<=n;i++)
        {
            num=sum=0;
            if(d[i]>0&&!vis[i])
            {
                dfs(i);
                if(num%2) ans+=sum;
            }
        }
        printf("%lld\n",ans);
    }
    return 0;
}