【LeetCode】304. Range Sum Query 2D - Immutable 解题报告（Python）

作者： 负雪明烛
id： fuxuemingzhu
个人博客： http://fuxuemingzhu.cn/

---

目录

• • 题目描述
  • 题目大意
  • 解题方法
  • • 预先求和
  • 相似题目
  • 参考资料
  • 日期

题目地址：https://leetcode.com/problems/range-sum-query-2d-immutable/description/

题目描述

Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

Note:

1. You may assume that the matrix does not change.
2. There are many calls to sumRegion function.
3. You may assume that row1 ≤ row2 and col1 ≤ col2.

题目大意

求二维数组中指定左上角和右下角的长方形内所有数字的和。给定的二维数组是不会变的，每次变得是求和的范围。

解题方法

预先求和

这个题肯定是用先把所有的和求出来，然后查找的时候直接计算就行了。我们使用的这个求和矩阵保存的是每个位置到整个矩阵的左上角元素这个矩形的所有元素和。为了方便起见，利用了和DP类似的添加边界的方法，也就是在最左边和最上边添加了全是0的列和行，这样能保证在求和的时候，每个位置的和是左边的和+上边的和+自身-左上元素的和。

即，我们已知sum(OD):

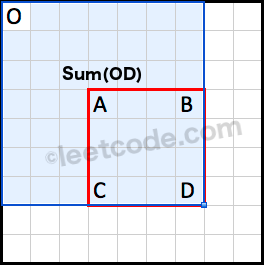
已知sum(OB):

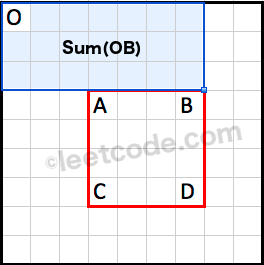
已知sum(OC):

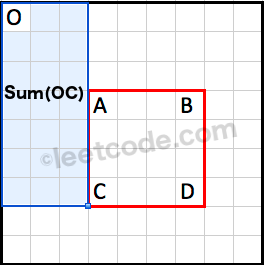
已知sum(OA):

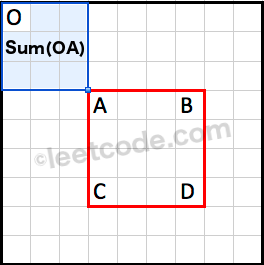
那么，矩形ABDC的面积：

Sum(ABCD)=Sum(OD)−Sum(OB)−Sum(OC)+Sum(OA)

计算原始求和矩阵时间复杂度是O(MN)，求面积时间复杂度是O(1)，空间复杂度是O(MN).

class NumMatrix(object):

    def __init__(self, matrix):
        """
        :type matrix: List[List[int]]
        """
        if not matrix or not matrix[0]:
            M, N = 0, 0
        else:
            M, N = len(matrix), len(matrix[0])
        self.sumM = [[0] * (N + 1) for _ in range(M + 1)]
        for i in range(M):
            for j in range(N):
                self.sumM[i + 1][j + 1] = self.sumM[i][j + 1] + self.sumM[i + 1][j]  - self.sumM[i][j] + matrix[i][j]

    def sumRegion(self, row1, col1, row2, col2):
        """
        :type row1: int
        :type col1: int
        :type row2: int
        :type col2: int
        :rtype: int
        """
        return self.sumM[row2 + 1][col2 + 1] - self.sumM[row2 + 1][col1] - self.sumM[row1][col2 + 1] + self.sumM[row1][col1]

# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)

相似题目

303. Range Sum Query - Immutable

参考资料

https://leetcode.com/articles/range-sum-query-2d-immutable/

日期

2018 年 10 月 30 日 —— 啊，十月过完了