上午小测3 T1 括号序列 && luogu P5658 [CSP/S 2019 D1T2] 括号树 题解

前 言：

一直很想写这道括号树。。毕竟是在去年折磨了我4个小时的题。。。。

上午小测3 T1 括号序列

前言：

原来这题是个dp啊。。。这几天出了好几道dp，我都没看出来，我竟然折磨菜。

考试的时候先打了个暴力，然后就开始往容斥上想。。。。

解析：

考虑dp。

令dp[i] 表示以i为结尾的，合法的子串数量。

令match[i] 表示进行括号匹配时，与i匹配的括号的编号。

（以上i都是右括号，如果是左括号置为0即可）

然后，就有： if(match[i]) dp[i]=dp[match[i]-1]+1;

这个转移方程的含义如下：

首先是前面的判断语句。必须是在i有匹配的情况下。

这样就排除了两种不可能的情况，一种是i是左括号，另一种是i是右括号，但在进行括号匹配时，没有与其匹配的左括号。

显然以上两种情况，i都不可能成为一个合法字串的结尾。

然后是要先给dp[i]加上1。这是以match[i]为起点，i为终点的子串的贡献。

其次要加上dp[match[i]-1];

这时分两种情况讨论。

第一种是 s[match[i]-1]==')' : 好丑的图

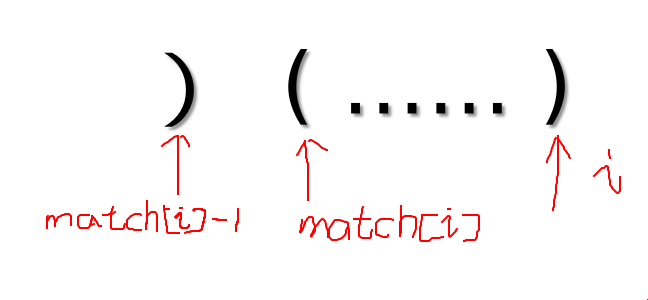
此时以i为结尾的子串还可能继续向左延伸，只要加上dp[match[i]-1]即可。

另外一种是 s[match[i]-1]=='（'：

此时不能继续向左延伸，所以不加，但是因为dp[match[i]-1]是0，所以加上也不会错（主要是这样写起来方便）

说的有些麻烦了，其实还是挺显然的。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1000000+10;
#define gc() (p1 == p2 ? (p2 = buf + fread(p1 = buf, 1, 1 << 20, stdin), p1 == p2 ? EOF : *p1++) : *p1++)
#define read() ({ register int x = 0, f = 1; register char c = gc(); while(c < '0' || c > '9') { if (c == '-') f = -1; c = gc();} while(c >= '0' && c <= '9') x = x * 10 + (c & 15), c = gc(); f * x; })
char buf[1 << 20], *p1, *p2;
char s[maxn];
int n,top;
int dp[maxn];
int match[maxn];
ll ans;
struct node{
	int pos;
	char c;
	node(){}
	node(int x,char y){
		pos=x;
		c=y;
	}
}Stack[maxn];
void Solve(){
	scanf("%s",s+1);
	n=strlen(s+1);
	Stack[++top]=node(1,s[1]);
	for(int i=2;i<=n;++i){
		if(s[i]==')'&&Stack[top].c=='('){
			node t=Stack[top];
			top--;
			match[i]=t.pos;
		}else Stack[++top]=node(i,s[i]);
	}
	for(int i=1;i<=n;++i){
		if(match[i]){
			dp[i]=1+dp[match[i]-1];
		}
	}
	for(int i=1;i<=n;++i) ans+=dp[i];
	printf("%lld\n",ans);
}
int main(){
	freopen("bracket.in","r",stdin);
	freopen("bracket.out","w",stdout);
	Solve();
	return 0;
}

luogu P5658 [CSP/S 2019 D1T2] 括号树

前言：

其实应该不是很难吧。。。

解析：

和上一道题类似，但不是完全相同废话

所以一定要看清题啊。。。

这次问的是每个字符串的合法子串数量。。。我当成以每个字符结尾的合法字串数量了，直接暴毙。。。

会上面那道题，这个就简单多了。

先令dp[i]表示以i结尾的合法字子串数量，然后求个树上前缀和就行了。

照上个题的思路，改改式子：

if(match[i]) dp[i]=dp[fa[match[i]]]+1

最后。。。

不开long long见祖宗！

代码:

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=500000+10;
#define gc() (p1 == p2 ? (p2 = buf + fread(p1 = buf, 1, 1 << 20, stdin), p1 == p2 ? EOF : *p1++) : *p1++)
#define read() ({ register int x = 0, f = 1; register char c = gc(); while(c < '0' || c > '9') { if (c == '-') f = -1; c = gc();} while(c >= '0' && c <= '9') x = x * 10 + (c & 15), c = gc(); f * x; })
char buf[1 << 20], *p1, *p2;
struct node{
	int to,nxt;
}edge[maxn<<1];
int head[maxn],fa[maxn],match[maxn];
ll dp[maxn];
char s[maxn];
struct Node{
	int pos;
	char c;
	Node(){}
	Node(int x,char y){
		pos=x;
		c=y;
	}
}Stack[maxn];
int n,cnt,top;
ll ans;
void add(int from,int to){
    edge[++cnt].to=to;
    edge[cnt].nxt=head[from];
    head[from]=cnt;
}
void dfs1(int u){
	Node t=Stack[top];
	if(t.c=='('&&s[u]==')'){
		match[u]=t.pos;
		top--;
		for(int i=head[u];i;i=edge[i].nxt){
			int v=edge[i].to;
			if(v==fa[u]) continue;
			dfs1(v);
		}
		Stack[++top]=Node(t.pos,t.c);
	}else{
		Stack[++top]=Node(u,s[u]);
		for(int i=head[u];i;i=edge[i].nxt){
			int v=edge[i].to;
			if(v==fa[u]) continue;
			dfs1(v);
		}
		top--;
	}
}
void dfs2(int u){
	if(match[u]) dp[u]=dp[fa[match[u]]]+1;
	for(int i=head[u];i;i=edge[i].nxt){
		int v=edge[i].to;
		if(v==fa[u]) continue;
		dfs2(v);
	}
}
void dfs3(int u,int f){
	dp[u]+=dp[f];
	for(int i=head[u];i;i=edge[i].nxt){
		int v=edge[i].to;
		if(v==fa[u]) continue;
		dfs3(v,u);
	}
}
void Solve(){
	scanf("%d%s",&n,s+1);
	for(int i=2;i<=n;++i){
		scanf("%d",&fa[i]);
		add(i,fa[i]);
		add(fa[i],i);
	}
	dfs1(1);
	dfs2(1);
	dfs3(1,0);
	for(int i=1;i<=n;++i) ans^=(1ll*i*dp[i]);
	printf("%lld\n",ans);
}
int main(){
	// freopen("brackets.in","r",stdin);
	// freopen("brackets.out","w",stdout);
	Solve();
	return 0;
}