7, java数据结构和算法: 八皇后问题分析和实现 , 递归回溯

什么是八皇后问题: 指的是,在一个8 * 8的棋盘中, 放置8个棋子, 保证这8个棋子相互之间, 不在同一行,同一列,同一斜线, 共有多少种摆法?

游戏连接: http://www.4399.com/flash/42643.htm#search3

直接上代码:

public class QueueLv8 {
    int maxSize =8;
    int[] array = new int[maxSize];
    static int count = 0;//正解次数
    static int okCount = 0;//判断次数

    public static void main(String[] args){
        //8皇后问题: 指的是,在一个8 * 8的棋盘中, 放置8个棋子, 保证这8个棋子相互之间, 不在同一行,同一列,同一斜线, 共有多少种摆法? 共有92种摆法

        //8皇后问题,  这里使用递归实现, 体现了回溯思想.
        //这里使用一维数组来实现,比如: int[8] = {0,4,7,5,2,6,1,3} ,表示:第i+1个皇后,放在棋盘的第i+1行,第 int[i]+1 列.  这里很重要,理解了这里,就能理解后面的算法
        // 第1个皇后 放在 第1行 第1列.   第二个皇后放在第2行第5列,  第三个皇后放在第三行第8列......

        /**
         * 实现思路:
         * 1: 先将第一个皇后 放在第一行第一列的位置上
         * 2: 再将第二个皇后 放在第二行的第一列位置上, 判断是否满足规则, 如果不满足, 将该皇后放到 第二行第二列位置上,判断是否满足规则, 依次将这个皇后放到第3列, 第四列,,,,第8列位置上,直到找到一个合适位置
         * 3: 再将第三个皇后 放到第三行的 第一列,,第二列,第三列,,,直到找到合适位置
         * 4: 直到将第8个皇后, 放到第8行的合适位置上,后,  此时算是找到一个正确的解.
         * 5: 当得到一个正确解时候,开始回溯,回退到上一行,将该行皇后位置向后一列移动,判断是否满足规则,,,, 最终回溯到第一行,将第一列位置时的全部正确解都拿到,然后第一行第一列该皇后位置,变为第二列,第三列,,,第8列, 此时得到所有的正确解
         */

        QueueLv8 queue8 = new QueueLv8();
        queue8.getQueue8Res(0);
        System.out.printf("8皇后总共有%d种摆法\n",count);
        System.out.printf("总共判断次数为:%d",okCount);
    }

    //写一个方法, 用来放置第 n 个皇后
    public void getQueue8Res(int n){//n表示第n个皇后,也表示第n行, 为0时表示,放置第一个皇后,在第一行,第一列上,  为1表示,放在第二行,第一列上
        //是否已完成
        if(n == maxSize){//当为8 时, 说明要放置第9个皇后了,已结束
            print();
            return;
        }

        //一进来这里是 0-8的循环,就说明,每个棋子,都要从第1列到第8列移动,从而找到合适位置
        for (int i = 0; i < 8; i++) {
            //先将这个皇后放在第1列上
            array[n] = i;
            //判断是否符合规则
            if(IsOk(n)){
                //为true 表示 符合规则, 不在同一行,同一列,同一斜线
                getQueue8Res(n+1);
            }
            //如果不符合规则,在同一行,或同一列,或同一斜线, 此时i++, 表示将该皇后放到下一列,再判断是否符合规则
        }

    }

    //判断是否满足规则, 其实就是判断 这个棋子,和之前的棋子,是否同一行,同一列,是否同一斜线
    public boolean IsOk(int n){//n 表示第n个皇后, 同时n 也表示了行数,n始终在变,所以不用判断是否在同一行
        okCount++;
        for (int i = 0; i < n; i++) {
            //判断是否在 同一列, array[n] == array[i] 这个代码表示, 在这个皇后和 之前的0到n-1个皇后中有一个是在同一列,  比如int[8] = {0,4,0,5,2,6,1,3} ,第3个皇后和 第1个皇后就在同一列, n=2, i=0  array[n] == array[i]
            //判断是否在 同一斜线,  Math.abs(n-i) == Math.abs(array[n] - array[i]) ,这行代码表示,这个皇后和 之前的之前的0到n-1个皇后中有一个是在同一斜线.  比如int[8] = {0,4,2,5,2,6,1,3} 第3个皇后和 第1个皇后就在同一斜线上, 此时 n = 2, i = 0 ,Math.abs(2-0) == Math.abs(array[2] - array[0]) 成立, 用的是绝对值,所以不管是正斜线,还是反斜线都是成立的, 还可以将他理解成 等边直角三角形的 二个边是相等的,所以在同一斜线上
            if(array[n] == array[i] || Math.abs(n-i) == Math.abs(array[n] - array[i])){
                return false;
            }
        }
        return true;
    }

    public void print(){
        count++;
        for (int i = 0; i < array.length; i++) {
            System.out.printf(array[i]+" ");
        }
        System.out.println();
    }
}

测试结果:

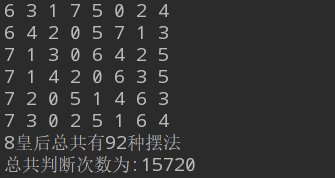
从这个结果是可以看出来 : 他是先找到 第一行第一列棋子所在位置的所有正解,之后, 再得到第2列,,,第三列,,第八列