P5960 【模板】差分约束算法

题目描述

给出一组包含 $m$ 个不等式，有 $n$ 个未知数的形如：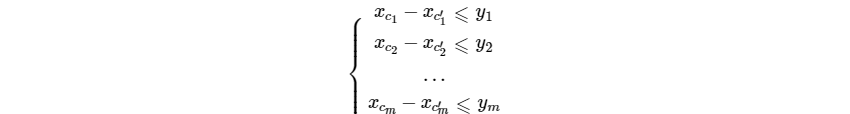

的不等式组，求任意一组满足这个不等式组的解。

输入格式

第一行为两个正整数 $n,m$，代表未知数的数量和不等式的数量。

接下来 $m$ 行，每行包含三个整数 $c,c',y$，代表一个不等式 $x_c-x_{c'} \leqslant y$。

输出格式

一行，$n$ 个数，表示 $x_1​,x_2​⋯x_n$​ 的一组可行解，如果有多组解，请输出任意一组，无解请输出$NO$。

样例数据

输入

3 3
1 2 3
2 3 -2
1 3 1

输出

5 3 5

分析

将$0$与每个点连一条长度为$0$的边，以$0$为起点求单源最短路，如果判断有负环那么该组不等式无解，否则$x_i=Dis_i$就是一组解

代码

#include <bits/stdc++.h>

#define Enter puts("")
#define Space putchar(' ')

using namespace std;

typedef long long ll;
typedef double Db;

inline ll Read()
{
    ll Ans = 0;
    char Ch = getchar() , Las = ' ';
    while(!isdigit(Ch))
    {
        Las = Ch;
        Ch = getchar();
    }
    while(isdigit(Ch))
    {
        Ans = (Ans << 3) + (Ans << 1) + Ch - '0';
        Ch = getchar();
    }
    if(Las == '-')
        Ans = -Ans;
    return Ans;
}

inline void Write(ll x)
{
    if(x < 0)
    {
        x = -x;
        putchar('-');
    }
    if(x >= 10)
        Write(x / 10);
    putchar(x % 10 + '0');
}
const int N = 1000000;

int n , m;
int Count[N] , Dis[N] , Head[N];
int Total = 0;
bool Visit[N] , t;

queue <int> Q;

struct Edge
{
    int Dis;
    int Next;
    int To;
}E[2 * N];

inline void Add_Edge(int u , int v , int w)
{
    E[++Total].Dis = w;
    E[Total].To = v;
    E[Total].Next = Head[u];
    Head[u] = Total;
}

inline bool SPFA()
{
    for(int i = 0; i <= n; i++)
    {
        Visit[i] = 0;
        Dis[i] = 1e6;
    }
    Visit[0] = 1 , t = 0 , Dis[0] = 0;
    Q.push(0);
    while(!Q.empty())
    {
        int u = Q.front();
        Q.pop();
        Visit[u] = 0;
        for(int i = Head[u]; i;i = E[i].Next)
        {
            int v = E[i].To , w = E[i].Dis;
            if(Dis[v] > Dis[u] + w)
            {
                Dis[v] = Dis[u] + w;
                if(Count[v] >= n)
                    return false;
                if(!Visit[v])
                    Visit[v] = 1 , Count[v]++ , Q.push(v);
            }
        }
    }
    return true;
}

int main()
{
    n = Read() , m = Read();
    for(int i = 1; i <= m; i++)
    {
        int u = Read() , v = Read() , w = Read();
        Add_Edge(v , u , w);
    }
    for(int i = 1; i <= n; i++)
        Add_Edge(0 , i , 0);
    if(SPFA() == false)
        puts("NO");
    else
        for(int i = 1; i <= n; i++)
            Write(Dis[i]) , Space;
    return 0;
}