算法入门 - 基于动态数组的栈和队列(Java版本)

之前我们学习了动态数组的实现，接下来我们用它来实现两种数据结构——栈和队列。首先，我们先来看一下栈。

什么是栈？

栈是计算机的一种数据结构，它可以临时存储数据。那么它跟数组有何区别呢？

我们知道，在数组中无论添加元素还是删除元素，都可以根据索引位置或值进行操作，栈是否也支持这样的操作呢？答案是不行，栈最大的特点就是后进先出（Last In First Out, LIFO）：

栈虽然看似简单，但是在计算机世界中有着非常重要的作用。比如在连续调用时，就利用了栈的特性：

    public static void addNum(){
        System.out.println("加法运算");
        Scanner scanner = new Scanner(System.in);
        System.out.print("请输入整数a：");
        int a = scanner.nextInt();
        System.out.print("请输入整数b：");
        int b = scanner.nextInt();
        System.out.println("a + b = " + (a + b));
    }

    public static void main(String[] args) {
        addNum();
    }

这里，在调用 addNum 方法时，内部又依次调用了两次 Scanner 实现输入。所以可以这么看，先调用了 addNum 方法，但是必须等待两次 Scanner 调用完成后，addNum 方法才能结束：

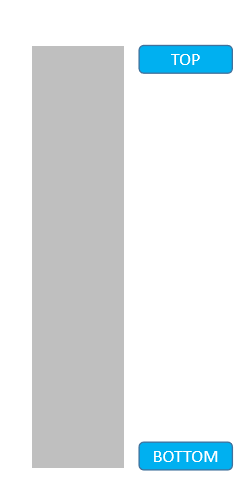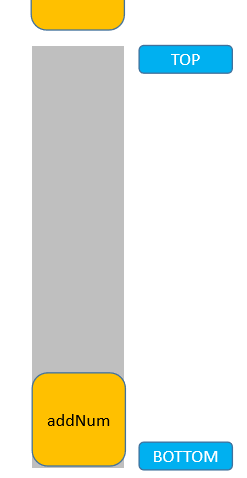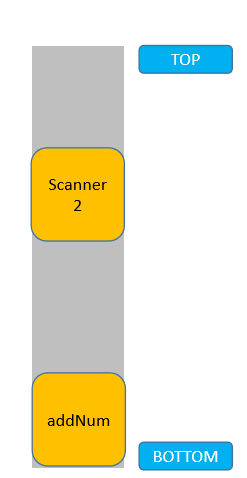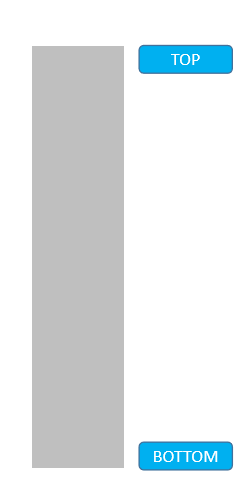
了解了栈后进先出的特点，我们就可以使用动态数组进行模拟了。

使用动态数组模拟栈

模拟的关键点在于“后进”和“先出”，也就是说，如果使用数组模拟的话，入栈时需要从数组尾部添加元素（addLast），出栈时也从尾部出栈（removeLast）：



所以这样一来，数组头部实际上是栈底，数组尾部是栈顶。

接下来我们就用代码实现。

代码实现

首先定义栈的接口，规范栈的操作：

package com.algorithm.stack;

public interface Stack <E> {
    void push(E element);   // 入栈
    E pop();                // 出栈
    E peek();               // 查看栈顶元素
    int getSize();          // 获取栈长度
    boolean isEmpty();      // 判断栈是否为空

}

按照刚才说的，只要分别使用动态数组的 addLast() 和 removeLast() 方法替代栈的 push() 和 pop() 方法即可：

package com.algorithm.stack;

import com.algorithm.dynamicarrays.Array;

// 使用动态数组实现栈结构
// 栈底: index = 0; 栈顶: index = size - 1 (push: O(1), pop: O(1))
// 如果栈顶设在index=0的位置，push和pop都将面临较大开销(O(n))
public class ArrayStack<E> implements Stack<E>{
    private Array<E> arr;    // 使用之前实现的Array动态数组模拟栈

    public ArrayStack(int capacity){
        arr = new Array<>(capacity);
    }

    public ArrayStack(){
        arr = new Array<>();
    }

    // 从栈顶压入
    @Override
    public void push(E element){
        arr.addLast(element);
    }

    // 从栈顶弹出
    @Override
    public E pop(){
        return arr.removeLast();
    }

    // 从栈顶返回
    @Override
    public E peek(){
        return arr.getLast();
    }

    // 栈长度
    @Override
    public int getSize(){
        return arr.getSize();
    }

    // 栈容量
    public int getCapacity(){
        return arr.getCapacity();
    }

    // 判断栈是否为空
    @Override
    public boolean isEmpty(){
        return arr.isEmpty();
    }

    @Override
    public String toString(){
        StringBuilder str = new StringBuilder();
        str.append(String.format("Stack: size = %d, capacity = %d\n[", getSize(), getCapacity()));
        for (int i=0; i<getSize(); i++) {
            str.append(arr.get(i));
            if (i < getSize() - 1) {
                str.append(", ");
            }
        }
        str.append("] top");    // 标识出栈顶位置
        return str.toString();
    }

    // main函数测试
    public static void main(String[] args) {
        ArrayStack<Integer> arrayStack = new ArrayStack<>();
        for (int i =0; i<5; i++){
            arrayStack.push(i);
            System.out.println(arrayStack);
        }
        // pop
        arrayStack.pop();
        System.out.println(arrayStack);
    }
}

/*
输出结果：
Stack: size = 1, capacity = 10
[0] top
Stack: size = 2, capacity = 10
[0, 1] top
Stack: size = 3, capacity = 10
[0, 1, 2] top
Stack: size = 4, capacity = 10
[0, 1, 2, 3] top
Stack: size = 5, capacity = 10
[0, 1, 2, 3, 4] top
Stack: size = 4, capacity = 10
[0, 1, 2, 3] top
*/

结果符合预期。

栈的时间复杂度分析

入栈对应的数组操作是 addLast()，我们可以通过查看该方法的具体实现进行分析：

    /**
     * 在指定位置添加元素
     * 指定位置处的元素需要向右侧移动一个单位
     * @param index   索引
     * @param element 要添加的元素
     */
    public void add(int index, E element) {
        if (index < 0 || index > size) throw new IllegalArgumentException("Illegal index, index must > 0 and <= size!");
        // 数组满员触发扩容
        if (getSize() == getCapacity()) {
            resize(2 * getCapacity());  // 扩容为原数组的2倍
        }
        // 从尾部开始，向右移动元素，直到index
        for (int i = getSize() - 1; i >= index; i--) {
            data[i + 1] = data[i];
        }
        // 添加元素
        data[index] = element;
        size++;
    }

    // 数组尾部添加元素
    public void addLast(E element) {
        add(getSize(), element);
    }

    /**
     * 删除指定位置元素
     * 通过向左移动一位，覆盖指定位置处的元素，实现删除元素(data[size - 1] = null)
     * @param index 索引
     */
    public E remove(int index) {
        if (index < 0 || index > size) throw new IllegalArgumentException("Illegal index, index must > 0 and < size!");
        // 数组长度为0时抛出异常
        if (getSize() == 0) throw new IllegalArgumentException("Empty array!");
        E removedElement = data[index];
        // 向左移动元素
        for (int i = index; i < getSize() - 1; i++) {
            data[i] = data[i + 1];
        }
        // 将尾部空闲出的位置置为空，释放资源
        data[getSize() - 1] = null;
        size--;
        // size过小触发数组缩减
        if (size == getCapacity() / 4 && getCapacity() / 2 != 0) resize(getCapacity() / 2);
        return removedElement;
    }

    // 删除尾部元素
    public E removeLast() {
        return remove(getSize() - 1);
    }

可以看出，每次从数组尾部添加元素时，add() 方法的 for 循环都无法满足条件，等同于直接在 size 处添加元素，所以时间复杂度为 O(1)。如果再考虑数组满员后触发的 resize 操作，相当于是进行了 n+1 次 add() 操作后才会触发 n次操作的 resize（移动n个元素至新数组），所以每次 add() 操作平均耗时为 \(\frac{2n+1}{n+1} \approx 2\)，是一个与数组长度 n 无关的数，所以也可以看做是 O(1) 复杂度的。

同理，出栈对应的 removeLast() 的时间复杂度也是 O(1)。

什么是队列？

理解了栈后，队列就更简单了。实际上，队列是我们日常生活中几乎每天都会碰到的。我们去超市买东西结账时需要排队，去银行办理业务时需要排队，做核酸、打疫苗就更需要排队了:



所以队列是一种先进先出的数据结构。

使用动态数组模拟队列

如果将队列也转换成数组，会是这样：



可以看出，入队的操作与入栈的实现方式相同，而出队则是从数组头部（removeFirst）。

代码实现

同样，我们先定义队列接口：

package com.algorithm.queue;

public interface Queue<E> {
    void enqueue(E element);    // 入队
    E dequeue();                // 出队
    E getFront();               // 获取队首元素
    int getSize();              // 获取队列长度
    boolean isEmpty();          // 判断队列是否为空
}

package com.algorithm.queue;

import com.algorithm.dynamicarrays.Array;

// 使用动态数组实现队列
public class ArrayQueue<E> implements Queue<E>{
    private Array<E> arr;    // 使用之前实现的Array动态数组模拟队列

    public ArrayQueue(int capacity){
        arr = new Array<>(capacity);
    }

    public ArrayQueue(){
        arr = new Array<>();
    }

    // 队首: index = 0; 队尾: index = size - 1
    // 队尾入队
    @Override
    public void enqueue(E element){
        arr.addLast(element);
    }

    //队首出队
    @Override
    public E dequeue(){
        return arr.removeFirst();
    }

    // 队首返回
    @Override
    public E getFront(){
        return arr.getFirst();
    }

    // 队列长度
    @Override
    public int getSize(){
        return arr.getSize();
    }

    // 判断队列是否为空
    @Override
    public boolean isEmpty(){
        return arr.isEmpty();
    }

    // 队列容量
    public int getCapacity(){
        return arr.getCapacity();
    }

    @Override
    public String toString(){
        StringBuilder str = new StringBuilder();
        str.append(String.format("Queue: size = %d, capacity: %d\ntop [", getSize(), getCapacity()));
        for (int i=0; i< getSize(); i++) {
            str.append(arr.get(i));
            if (i< getSize() - 1) {
                str.append(", ");
            }
        }
        str.append("] tail");    // 标识队尾
        return str.toString();
    }

    // main函数测试
    public static void main(String[] args) {
        ArrayQueue<Integer> arrayQueue = new ArrayQueue<>();
        for (int i=0;i<5;i++){
            arrayQueue.enqueue(i);
            System.out.println(arrayQueue);
            if (i % 3 == 2){    // 每隔3个元素进行出队操作
                arrayQueue.dequeue();
                System.out.println(arrayQueue);
            }
        }
    }
}

/*
输出结果：
Queue: size = 1, capacity: 10
top [0] tail
Queue: size = 2, capacity: 10
top [0, 1] tail
Queue: size = 3, capacity: 10
top [0, 1, 2] tail
Queue: size = 2, capacity: 5
top [1, 2] tail
Queue: size = 3, capacity: 5
top [1, 2, 3] tail
Queue: size = 4, capacity: 5
top [1, 2, 3, 4] tail
*/

队列的时间复杂度分析

入队的时间复杂度与之前入栈相同，都是 O(1)；而出队由于是从数组头部出，所以会触发剩余元素向左移动，所以时间复杂度为 O(n)。

总结

通过对动态数组的学习，并实现了栈和队列两种比较基础的数据结构，让我们能够更深入的了解这些结构背后的原理，为我们今后学习更复杂的数据结构打下基础。