CF461D-Appleman and Complicated Task【并查集】

正题

题目链接:https://www.luogu.com.cn/problem/CF461D

---

题目大意

\(n*n\)的网格需要填上\(x\)或\(o\)，其中有\(k\)个格子已经固定，求有多少中填写方案使得每个格子的四周都有偶数个\(o\)。

---

解题思路

约束条件相当于一个格子周围的异或和都为\(0\)，也就是对于任意\((x,y)\)都有\(a_{x-1,y}\ xor\ a_{x,y-1}\ xor\ a_{x+1,y}\ xor\ a_{x,y+1}\)。也就是对于一个格子\((x,y)\)也有\(a_{x,y}=a_{x-1,y-1}\ xor\ a_{x-1,y+1}\ xor\ a_{x-2,y}\)

根据以上我们可以发现对于一个格子的值都可以由第一行的某些格子的异或和来表示，且它们格子的奇偶相同。

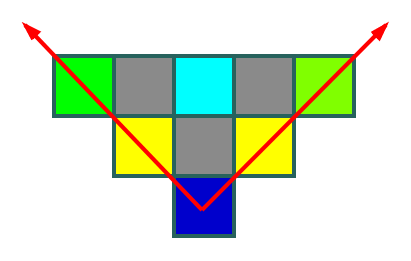
从这个蓝色格子来看，它的值等于黄色格子和青色格子的异或和。

其中两个黄色格子又都包括了青色格子，所以相互抵消，中间缺失的青色格子回本蓝色本身补回来，而周围的绿色格子不会被抵消。

所以能够发现其实蓝色格子的异或和就等于某一行里被红线夹着的同奇偶的格子的异或和。

这样我们对于一个固定的点就相等于限制奇或偶的一个区间异或值。

差分完之后就变为了判断两个格子是否相等，用并查集判即可。

---

code

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2e5+10;
const long long P=1e9+7,inv2=(P+1)/2;
int n,k,fa[N];
int find(int x)
{return (fa[x]==x)?x:(fa[x]=find(fa[x]));}
bool Calc(int l,int r,int w){
    if(w){
        if(find(l)==find(r))return 0;
        if(find(l)==find(r+n))return 1;
        fa[find(r+n)]=find(l);
        fa[find(l+n)]=find(r);
    }
    else{
        if(find(l)==find(r+n))return 0;
        if(find(l)==find(r))return 1;
        fa[find(r)]=find(l);
        fa[find(r+n)]=find(l+n);
    }
    return 1;
}
int main()
{
    scanf("%d%d",&n,&k);
    int p=n;n+=2;
    for(int i=1;i<=2*n;i++)fa[i]=i;
    for(int i=1;i<=k;i++){
        int x,y;char w[2];
        scanf("%d%d%s",&x,&y,&w);x--;y--;
        int l=abs(x-y),r=min(x+y,2*(p-1)-x-y)+2;
        if(!Calc(l,r,w[0]=='o'))
            return puts("0")&0;
    }
    long long ans=inv2*inv2%P,z=0;
    for(int i=0;i<2*n;i++)
        if(find(i)==i)z++;z/=2;
    while(z)z--,ans=ans*2%P;
    printf("%lld\n",ans);
    return 0;
}