矩阵QR分解

1 orthonormal 向量与 Orthogonal 矩阵

orthonormal 向量定义为 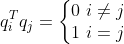，任意向量  相互垂直，且模长为1；

如果将  orthonormal 向量按列组织成矩阵，矩阵为 Orthogonal 矩阵，满足如下性质：

；

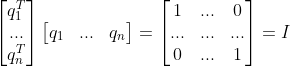当 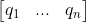为方阵时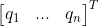，为其逆矩阵；当  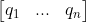为长方形矩阵时，为其左逆；

当矩阵 Q 为正交矩阵时，对向量变换变换前后点积不发生改变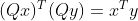，，证明如下：

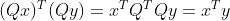，当 x = y 时，有  。

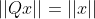对任意向量 b ，可以分解为一组正交向量的线性组合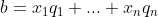，，要求解系数x，可先写成矩阵形式：

，， ；

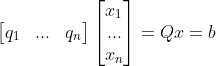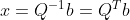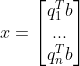因此，向量 b 可分解为  。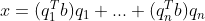

2 Gram-Schmidt 与 QR 分解

对矩阵 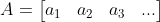，可以将其转换为正交矩阵 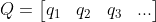，方法如下：

1）向量 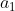 方向保持不变，将其长度归一化， ；

2）向量 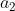 可分解为向量  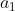投影分量与垂直于向量  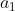 的两分量，剔除投影分量得 ，；

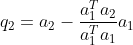3）同理，剔除向量 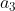 在 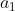 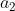，  上投影分量得 ， ；

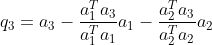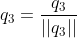4）依照如上方法，可以对所有向量完成正交化。

以上处理可以使用矩阵表示，矩阵 Q 为矩阵 A 的列进行线性变换结果，故可写为 A=QR 。

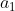1）向量   与向量 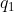具有相同方向，故可表示为  ；

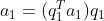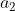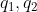2）向量  被分解为  方向向量，可表示为 ；

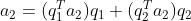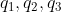3）向量  被分解为  方向向量，可表示为  ；

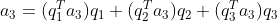4）综上表示为矩阵形式  。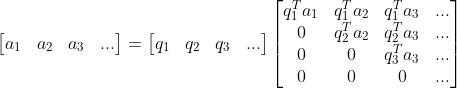

3 求解 Ax=b

使用 Gram-Schmidt 可将矩阵 A 转换为正交矩阵 Q，正交矩阵 Q 可简化 Ax=b 运算：

1）最小二乘法求解 ；

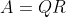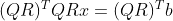2）带入  得 ，化简得 ；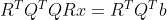

3）不管长方形矩阵还是方阵，都有 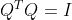，故上式可化简为 ；

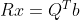4）由于 R 为上三角矩阵，使用回代法即可求解。

4 函数空间

向量 QR 分解可以推广到函数，向量内积表示各分量乘积之和，对于连续函数可表示为 ，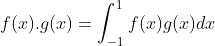

函数长度可表示为 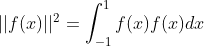，使用函数内积与函数长度定义，可以对函数按向量投影方法进行类似分解。

1）最小二乘法求解近似函数

给定函数 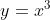，求解在区间 上的二阶近似函数 。

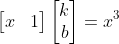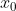a. 令 ，表示在区间  上，对于任意  都有  ；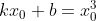

b. 使用最小二乘法得 ， ；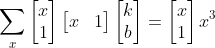

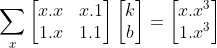c. 转换为积分得 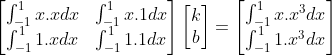，可求解 k, b 。

2）Legendre polynomials

以上方程 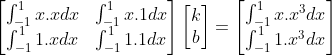  使用高斯消元法求解，但随着多项式次数增加，消元法会产生很大的截断误差。

使用 Gram-Schmidt 方法，将各个多项式基转换为正交函数，可以简化运算。

设原始多项式基为 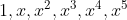，可做如下变换：

a. 保持第一个函数方向不变，对长度进行归一化处理，；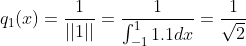

b. 函数 x 与函数 1 在区间  上正交，故仅需对长度归一化，；

c. 函数 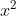 与函数 x 和 1 在区间   上均不正交，减去投影分量使其正交，

，，

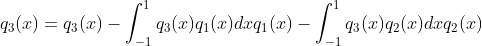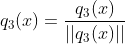带入求解得 ；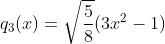

d. 使用同样方式求得 ， 。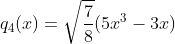

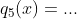通过以上函数基，任意多项式可以改写为以上函数基的线性组合。当仅使用几个低阶函数基表示时，类似线性代数投影近似。

对给定函数 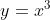，求解在区间 上的二阶近似函数  使用多项式函数基求解如下：

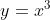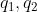函数  在  上投影为：

；

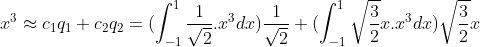整理得 。

3）傅里叶级数

函数的傅里叶级数使用三角函数为基线性展开，三角函数是互相正交的，当进一步对其归一化后构成一组函数基。任意函数被三角函数分解为：

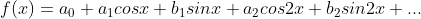，对应系数为函数与归一化三角函数内积

，。

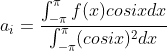参考资料 Linear Algebra And Its Applications   Gilbert Strang

Gram-Schmidt for functions: Legendre polynomials  S. G. Johnson, MIT course 18.06